隧道掌子面稳定性分析的一种简化方法
2019-04-15顾博渊白浪峰刘燕鹏
顾博渊,白浪峰,徐 平,刘燕鹏
(中交第一公路勘察设计研究院有限公司,陕西 西安 710075)
0 引 言
近年来,在中国经济快速增长的背景下,国家对交通行业大力投入,使中国公路交通行业得到了迅猛发展。截至2016年底,中国隧道共计23 707.9 km、19 516处,较2015年增幅分别达到10.99%、9.10%,无论是长度还是数量都已位居世界第一。
随着隧道总长和数量的全面增长,隧道修建过程中遇到穿越软弱破碎围岩[1-2]和古滑坡体[3-4]等不良地质现象的隧道工程实例不断增加。在这些地区修建隧道时,如何控制掌子面稳定并采取及时、有效的预加固措施一直是隧道工程设计和施工领域的一大难点。目前,隧道掌子面稳定分析已经引起广大隧道工作者的关注,并在理论分析、数值计算两方面得到很多有益的成果[5-11]。
在理论分析方面,Müller-Kirchenbauer提出掌子面微稳定模型,主要适用于由颗粒状物质构成的掌子面稳定分析,此种围岩具有非常低的黏聚力。Davis等[12]运用极限平衡法来分析隧道掌子面的稳定性,构建了4种有效的浅埋隧道拱顶塌方模式,计算了隧道在不排水情况下的稳定系数上限解。Broere[13]为分析开挖面前方土层的非均质性对滑动面的角度和掌子面稳定性的影响,提出了考虑隧道开挖范围内土体分层现象的三维楔形体计算模型。
在数值计算方面,中南大学阳军生等[14]为研究浅埋隧道掌子面稳定性及获取精细化的破坏模式,提出了一种上限有限元非结构化网格自适应加密策略。兰州交通大学郭桃明等[15]针对黄土地区山岭双线隧道软弱围岩稳定性较差的问题,采用ADINA软件进行了三维分析。梅洪斌[16]采用有限元方法对隧道圆形衬砌采用管棚法加固后各施工阶段的合理开挖进尺进行了三维分析。黄锋等[17]对不同开挖循环进尺条件下的全断面法隧道施工过程中横断面及地表位移响应规律进行了数值分析。周雪铭[18]就岩溶条件下隧道开挖对溶洞处治结构的影响进行了数值分析。张胜等[19]采用数值模拟的方法就不同工法对既有隧道的施工影响开展了研究。李围[20]针对高速公路连拱隧道施工方法进行了数值计算分析。
掌子面稳定分析是一个三维问题,运用数值分析技术虽然可以模拟整个施工过程及掌子面的破坏机理,但由于时效性较差,很难及时得出隧道掌子面支护的安全系数,不利于隧道施工期间掌子面稳定性判断、工程整体控制。本文基于楔形块体平衡理论,提出一种快速、准确评估软弱围岩隧道浅埋段掌子面稳定性的计算公式。这种计算模式考虑了围岩黏聚力、摩擦角、泊松比、土压力、开挖进尺、三维空间效应对掌子面稳定的影响,对隧道工程设计和施工具有很大的指导意义。
1 楔形块体计算模型
当开挖破碎围岩隧道浅埋段时,由于埋深浅、围岩差且没有自稳能力,发生掌子面失稳的可能性很大。本文基于楔形块体理论来分析隧道掌子面的稳定性,块体在土压力的作用下有向隧道内滑动的趋势(图1)。应用楔形块体理论计算时,基于面积相等原则,把隧道上台阶椭圆形横断面简化为矩形截面(见图2、3,图中C为隧道埋深,H为隧道上台阶开挖高度,B为等效矩形宽度,lu为掌子面距初期支护的距离)。

图1 楔形块体模型

图2 简化计算模型纵断面

图5 层状楔形块体的力学分析
1.1 块体计算公式推导
运用3D模型来研究楔形块体在土压力下的失效机理,作用在块体上的力分为驱动力和抵抗力,驱动力迫使块体滑向隧道内,抵抗力则给块体提供稳定性。

根据块体的力学平衡可以得出作用在掌子面上的土压力E(i),即维持掌子面稳定所需的最小支护力S(i)。
根据切片水平和竖直方向的力学平衡可得
E(i)+2T(i)cosθ(i)+(K(i)+R(i))cosθ(i)-
N(i)sinθ(i)=0
(1)
(K(i)+R(i))sinθ(i)-N(i)cosθ=0
(2)
考虑连续性条件
(3)
边界条件
(4)
可得
(5)
其中ξ1=tanφcosθ-sinθ,ξ2=tanφsinθ+cosθ。
由式(5)可求得
(6)

块体上作用的土压力可由太沙基理论求得,即
(7)
基于上述理论,当E≤0时掌子面是稳定的。如果E>0,说明掌子面需要其他施工辅助措施来保证稳定性。掌子面稳定的安全系数由式(8)确定,安全系数SF不应小于1.1。值得注意的是,当E>0时支护力S必须大于E。
(8)
1.2 掌子面稳定辅助措施
常用的掌子面辅助措施有玻璃纤维锚杆和预留核心土,施作锚杆属于主动防护,预留核心土则是被动防护。
1.2.1玻璃纤维锚杆对掌子面的影响
当施作玻璃纤维锚杆后,锚杆提高了破碎围岩的黏聚力、摩擦角、抗压强度和变形模量。加固作用如图6所示。

图6 锚杆的加固作用
假设围岩的最大主应力不变,如果没有锚杆加固,开挖后曲线由1变为2,加固后则从1变成3,相应的岩体强度则从4变到5。本文仅考虑施作锚杆后对围岩黏聚力的提高,这样做是偏保守的。加固后的黏聚力可由式(9)、(10)求得。
cs=c+c1
(9)
(10)
式中:c为初始黏聚力;c1为黏聚力增量;cs为加固后的黏聚力;Nu为玻璃纤维锚杆的承载能力;Ak为锚杆的影响面积;φ为初始内摩擦角;γkc为锚杆可靠度系数,取1.5。
1.2.2 预留核心土对掌子面的影响
假定楔形块体推动核心土,在核心土将滑未滑时提供给掌子面最大支护力,最大支护力由被动土压力确定,核心土的横截面如图7所示。图中,b1为核心土下部宽度,b2为核心土上部宽度,h′为核心土高度。

图7 核心土横截面
核心土提供的支护力由式(11)计算。
(11)
2 算 例
黑山共和国南北高速公路KOSMAN隧道为一座双洞两车道分离式隧道,左右幅隧道净距30 m,累计总长为5 169 m。左洞长2 662 m,桩号为LK26+510~ LK29+172,最大埋深为239.57 m;右洞长2 507 m,桩号为RK26+723~ RK29+230,最大埋深为239.25 m。
KOSMAN隧道隧址区位于黑山北部山岭地带,海拔1 000~1 200 m,围岩主要为复理石,隧道进出口地貌见图8、9。

图8 KOSMAN隧道进口地貌

图9 KOSMAN隧道出口地貌
KOSMAN隧道浅埋段围岩松散,自稳能力差,易出现掌子面失稳、拱部坍方等,不利于隧道施工安全。鉴于此,本节利用楔形块体理论对KOSMAN隧道浅埋段掌子面的稳定性进行分析。
2.1 掌子面自稳能力分析
以隧道浅埋段围岩作为研究对象,根据现行《公路隧道设计规范》(JTG D70—2004),其掌子面楔形体尺寸及围岩物理参数具体见表1。
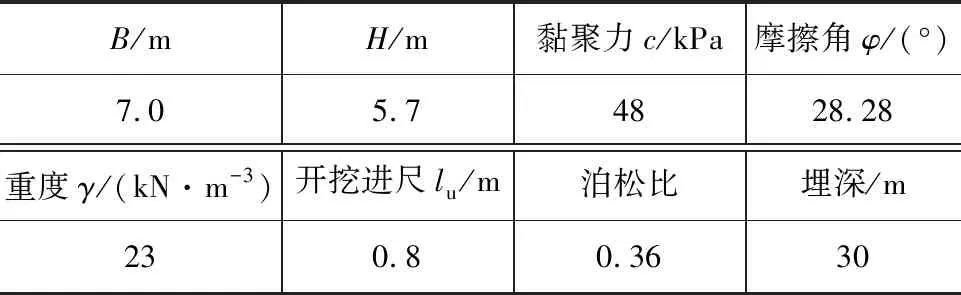
表1 掌子面楔形块体尺寸及围岩物理参数
块体上方承担的土柱压力为
作用在块体上的其他力为
由式(6)可求得维持掌子面稳定所需的支护力
E>0,说明在没有任何施工辅助措施的情况下掌子面是不稳定的,计算结果与现场实际情况一致。
2.2 施作玻璃纤维锚杆后掌子面的稳定性分析
掌子面施作玻璃纤维锚杆是维持掌子面稳定的常用方法,KOSMAN隧道现场玻璃纤维锚杆呈梅花形布置(图10),间距为2 m×2 m,锚杆承载能力为200 kN。锚杆对掌子面岩体加固后的黏聚力由式(9)、(10)求得,即

图10 掌子面施作玻璃纤维锚杆
由式(6)可求得维持掌子面稳定所需的支护力
支护力E<0,说明施作玻璃纤维锚杆后掌子面是稳定的,安全系数由式(8)求得,即
SF大于计算要求的1.1,说明利用玻璃纤维锚杆维持掌子面稳定是可行的。
2.3 预留核心土对掌子面稳定性的影响
施工预留核心土是维持掌子面稳定的常用方法,在KOSMAN隧道也进行了应用(图11)。预留核心土横截面呈梯形,上边宽度(b2)为3 m,下边宽度(b1)为4 m,核心土高度(h′)为2 m,核心土能提供的最大支护力由式(11)求得,即
1 573.12 kN
预留核心土后的安全系数由式(8)求得,即
掌子面安全系数SF大于计算要求的1.1,说明采取预留核心土方案施工对维持掌子面稳定是有效的。

图11 隧道掌子面预留核心土
2.4 控制掌子面稳定性辅助措施对比
根据上文计算结果,掌子面施作玻璃纤维锚杆和施工预留核心土均能满足施工对掌子面稳定性的要求。根据现场实际情况对二者的优劣进行对比。
(1)从对施工影响的角度而言,玻璃纤维锚杆易切割且不占据掌子面施工空间,而预留核心土方案会缩小掌子面施工空间,降低施工效率。
(2)从工程造价角度而言,玻璃纤维锚杆单价较高,大量使用会增加工程造价,而预留核心土方案施工时不会增加太多造价。
(3)从施工条件角度而言,玻璃纤维锚杆适应性较强,而采用预留核心土方案时,核心土应该满足施作系统锚杆所需最小的施工空间,核心土纵向长度应大于本身破裂面的长度,当采用临时仰拱(图12)时,不能采用核心土方案来保证掌子面的安全稳定性。

图12 隧道临时仰拱施工
3 结 语
本文依托黑山南北高速公路隧道项目,基于楔形块体理论,得到一种分析隧道掌子面稳定性的简化方法,通过本方法在黑山隧道施工期间的成功应用,为今后类似项目提供参考和依据的同时,也得到以下重要结论。
(1)KOSMAN隧道浅埋段掌子面在无施工辅助措施的情况下是不稳定的,计算结果与实际情况一致。
(2)掌子面施作玻璃纤维锚杆和施工时预留核心土均能满足施工对掌子面稳定性的要求,但玻璃纤维锚杆造价更高,预留核心土方案施工条件要求更高。
(3)结合KOSMAN隧道实际应用情况,本文所提出的评估软弱围岩隧道浅埋段掌子面稳定性的计算方法具有快速、简便、实用等优点,能够及时、有效地为现场施工提供技术指导。
