从函数图像绘制角度统一看四种内力图绘制
2019-04-14马志敏
马志敏


摘要:材料力学中内力图的绘制贯穿材料力学强度学习的整个过程,也是工程中结构分析重要的一环,因此,掌握好内力图的绘制,对于培养学生的工程分析能力至关重要。本文从数学函数图像绘制的角度,揭示了内力图绘制的本质,提出了四种内力图绘制的统一思想并小结了若干绘图技巧,以使学生能快速准确绘制内力图。
关键词:函数图像;内力图;截面法;面积法;控制面
中图分类号:G642.0 文獻标志码:A 文章编号:1674-9324(2019)10-0191-03
材料力学内力图的绘制是学生学习材料力学最开始接触到的内容,如何讲清这一内容,让学生能快速而准确地画出内力图,是很多材料力学主讲教师思考的热点问题。从数学的角度看,轴力、剪力、扭矩和弯矩四种内力,它们随着杆件截面位置的改变而变化,是关于杆件截面位置X的函数,内力图的绘制就是绘制这些函数的图像,这就是内力图的本质。本文从这一事实出发,提出了绘制函数图像的基本要素的概念,并归纳总结了确定内力图绘制所需的基本要素的方法,便于学生把握内力图的本质,深入了解各种内力图绘制技巧的来龙去脉,将所学知识融会贯通,巧记规律,从而快速准确绘制材料力学中的四种内力图。
一、内力函数特点和内力图绘制的基本要素
根据杆件受力的特点,从数学的角度看,内力函数往往是分段函数,回顾数学中分段函数图像的绘制过程,在这一过程中,要确定:(1)分段点位置;(2)每一段图像的形状:直线?斜线?抛物线?(现行材料力学教材中常出现的内力图形状)如果是抛物线,还需明确凸凹性和极值点,以及极值点位置。(3)每一段函数的起点、终点的处截面上的内力值,若有极值,尚需求出极值点截面上的内力值。
二、内力图绘制基本要素的确定
1.分段点位置。由截面法易知,在有集中力、集中力偶、分布荷载起点和终点处两边,内力函数是不一样的,因此,杆件的起点、终点、集中力、集中力偶、分布载荷起点和终点即是分段点位置。
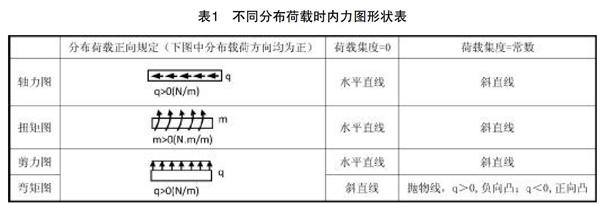
2.每一段内力图形状的确定。内力图的形状由内力与荷载集度之间的微分关系确定。现行材料力学书上主要推导了弯矩、剪力与荷载集度之间的微分关系,事实上,从数学函数的观点,也不难推导出轴力与荷载集度、扭矩与荷载集度也有与上面类似的微分关系,张宏学,马庆捷等人的论文中,均对此问题进行了详细的论述。根据这些微分关系,可以确定内力图的形状,具体见表1。
3.每一段函数起点、终点和极值点截面上内力的确定。在范钦珊主编《材料力学》教材中提出了控制面的概念,显然,两分段点间两控制面上的内力值,即为每段内力函数的起点和终点的值。由绘图经验可知,若内力图为水平直线,只需知晓起点、终点位置和任一截面上内力值即可绘制;若内力图为斜直线,由起点、终点两截面上内力值可绘制;若为抛物线,需确定起点、终点两截面上内力值,凸凹性,极值点位置(剪力为零处)及其内力值。下面将详细阐述这些控制面上的内力值的确定方法。
横截面上内力确定的方法,常用的有3种:截面法;面积法;突变规律。
(1)截面法。截面法是确定控制面上内力的基本方法,所有截面上的内力均可求,通用性好,尤其在受力比较简单的情况下,如无分布荷载作用,只受少数几个集中力(或力偶)作用时,用截面法灵活度高,方便快捷;同时截面法也是内力突变规律得出的基础,用截面法亦可推出很多实用的结论,如在梁的起点和终点处,若没有集中力偶作用,起点或终点处弯矩为零。但截面法的缺点是,当杆件受力较为复杂,分段较多时,控制面也较多,单纯用截面法求控制面上内力比较烦琐。
(2)面积法。面积法由分布荷载与内力之间的微分关系通过积分获得,具体见表2。用面积法可以方便确定同一段内力函数内,任一截面上的内力,如抛物线极值点处的内力值,或内力函数终点处的内力值。但面积法在运用时,必须通过其他方法先获得同一段内力函数
里面某一个截面上的内力值,这是面积法使用的前提条件。此外,在用面积法求横截面上弯矩值时,必须先画出剪力图。这一使用条件,在有些只需画弯矩图的应用中,形成不必要的麻烦。
(3)突变规律。这一规律适用于有集中力或集中力偶作用时的情形。由截面法分析易知,当有集中力或集中力偶作用时,集中力或集中力偶两侧控制面上的内力有突变,要么增加,要么减小,这就是“突变规律”。当集中力或集中力偶一侧控制面上的内力已知时,利用这一规律可快速确定另一侧控制面上的内力。集中力或集中力偶作用与其两侧控制面上内力的突变规律见表3。
三、内力图绘制的全过程
注:本文内力图的绘制,如无特殊说明,X轴均向右为正,从左往右画内力图。
内力图绘制步骤,以图1中例题为例,说明如下:
例:如图1所示外伸梁,在C处作用一矩Me=12kN.m的集中力偶,在BD段上作用集度q=4kN/m的均布载荷。试绘制梁的剪力图和弯矩图。
解:(1)计算支座反力。如图,可得:FA=5kN,FB=13kN;
(2)分段。以杆件起点、终点、集中力作用点、集中力偶作用点、分布载荷起点和终点作为杆件的分段点,分段点两侧无限接近截面即为控制面。由分析已知,内力图由AC、CB、BC三段内力函数图像组成。
(3)每一段函数图像起点、终点内力值确定。由于受力复杂,控制面较多,可用面积法和突变规律依次确定6个控制面上内力。
(4)函数图像形状判断。由表1规律确定。根据梁上所受力的情况,可知,对剪力图:AC、CB段为水平线;BD段为斜直线;对弯矩图:AC、CB段为斜直线,BD段为往正向凸的抛物线,且在D处取得极值。极值内力依然由面积法确定。经过以上4大步分析,最终绘制内力图如图1所示。
四、小结
内力图绘制的本质,是绘制分段函数的图像,每一段函数图像的绘制一定离不开起点值、终点值和函数图像形状这三个基本因素。在内力图绘制过程中,如何能快速确定每一段函数的起点值和终点值(即各控制面上的内力值)是快速画出内力图的关键。确定控制面上内力值的方法,本文主要介绍了3种方法,这3種方法的使用特点、优缺点、使用局限性等,本文进行了详尽的论述。截面法,由于在复杂受力情况下确定控制面上内力的烦琐,在研究快速绘制内力图时往往被忽视,这是不可取的。因为对特殊简单荷载情况,直接用截面法思想确定控制面上的内力反而是更快捷的,如无分布载荷作用,只有集中力作用的拉压杆,梁等。因此在实际教学中,不可过于强调某一种方法的便捷性,而应把握内力图绘制的基本要素和本质,根据具体情况,灵活选用控制面内力计算方法,以又快又好地绘出内力图。
参考文献:
[1]范钦珊.材料力学[M].第2版.北京:高等教育出版社,2006.
[2]张宏学,姚卫粉.材料力学内力图的统一画法[J].大众科技,2012,14(9):123-125.
[3]马庆捷,王晓玲,司玉兰,王军,郭福会.微分关系在画内力图中的应用[J].吉林化工学院学报,2002,19(2):58-60.
[4]朱惠莲.构件内力的简便算法和内力图的简便画法[J].漳州职业大学学报,2002,(3):44-47.
[5]于彩敏.浅谈材料力学中内力图的规律画法[J].价值工程,2015,(33):210-211.
A Unified View of Drawing Four Internal Force Diagrams from Functional Image Drawing Angle
MA Zhi-min
(School of Mechanical& Electrical Engineering,Wuhan Institute of Technology,Wuhan,Hubei 430073,China)
Abstract:The drawing of internal force diagrams in material mechanics runs through the entire process of material mechanical strength learning,and is also an important part of the structural analysis in the project.Therefore,mastering the drawing of internal force diagrams is very important for cultivating students' engineering analysis ability.This article reveals the essence of internal force diagram drawing from the perspective of mathematical function image drawing,proposes unified ideas of four internal force diagram drawing,and summarizes some drawing techniques,so that students can draw internal force diagrams quickly and accurately.
Key words:Function image;diagram of internal force;Cross section method;Area method;control section
