向量多项式优化问题的数值方法
2019-04-14彭雪珂周光明赵文杰
彭雪珂,周光明,赵文杰
(湘潭大学数学与计算科学学院,湖南 湘潭 411105)
最近几十年来,向量优化的理论与方法被广泛应用于金融、管理和最优决策等领域.向量优化问题的提出最早源于经济学.1896年,经济学家Pareto[1]将许多不好比较的目标从政治经济学的角度归纳为多目标规划问题.随后,他提出的Pareto最优解[2]概念极大地促进了向量优化问题的发展.1951年,Koopmans[3]首次提出Pareto有效解概念.同年,Kuhn等[4]在提出向量优化问题的Pareto最优解的同时,还对该解存在的充分和必要条件进行了研究.之后,向量优化理论问题受到了学者们的关注,并获得了许多重要的研究成果[5-10].
多项式优化是一类重要的非线性规划,关于这类优化问题的局部最优研究可以参考非线性规划中的研究方法.许多学者专注于探讨该类问题的全局优化[11-14].近些年,学者们还对其理论与算法进行了研究[15-22].目前,求解多项式全局优化问题主要有SOS方法和Lasserre松弛方法.当向量优化问题中的目标函数和约束条件都由多项式描述时,称之为向量多项式优化问题.笔者拟采用Lasserre松弛方法得到向量多项式优化问题的最优解.Lasserre松弛方法在满足一定秩条件的时候可以得到原多项式问题的最优值,且Lasserre[14]已证明下界序列的收敛性.该方法对于求解具有多项式特性的问题非常有效.
1 预备知识
向量优化问题的一般形式为[5]
minf(x)=(f1(x),f2(x),…,fk(x))T,
s.t.gj(x)≥0j=1,2,…,p,
hr(x)=0r=1,2,…,q.
(1)
其中:x=(x1,…,xn)T为n维决策变量;fi(x)(i=1,…,k),gj(x)(j=1,…,p),hr(x)(r=1,…,q)都是Rn→R的连续向量函数.记约束集合
K∶={x∈Rn|gj(x)≥0,j=1,…,p,hr(x)=0,r=1,…,q}.
(2)
从纯粹的数学角度出发,向量优化问题的“最优解”与通常数值意义上比较大小的概念有所区别,它表示均衡或者“非劣”.因此,引入非劣解(也称为有效解),它表示不劣于可行解集中的任何一个解.
定义1[5]设x*∈K,若对于∀x∈K,有fi(x*)≤fi(x)(i=1,2,…,k),则称x*为问题(1)的绝对最优解.
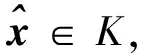
考虑一类特殊的向量优化问题.即问题(1)中的目标函数和约束条件都是由多项式描述的,fi(x)∈R[x](i=1,2,…,k),gj(x)∈R[x](j=1,2,…,p),hr(x)∈R[x](r=1,2,…,q)均为实多元多项式,称这样的问题为向量多项式优化问题.为了描述的方便,记为
(3)
假设fi(x)的最高次数为mi(i=1,2,…,k),实值多项式gj(x)次数不超过wj(j=1,2,…,p),实值多项式hr(x)次数不超过vr(r=1,2,…,q).
对于一般的多项式优化问题,Lasserre[14]提出了松弛优化方法.即利用矩-SOS松弛将原问题转化为半定规划问题(SDP),并通过求解一系列的SDP问题,得到一个单调递增收敛于原问题全局最优值的下界序列.
令
(4)
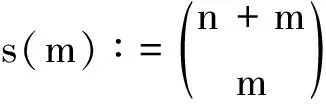
(5)

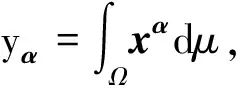
给定一个实值多项式p(x)∈R[x],考虑如下带约束多项式优化问题:
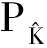
(6)
其中:p(x)的最高次数为m;
(7)

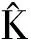
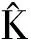

s.t.MN(y)0,
并证明了如下结果:
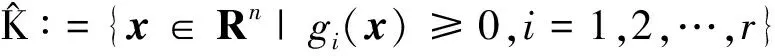
2 向量多项式优化问题的数值方法
笔者基于求解多项式优化问题的Lasserre松弛方法[14],以及求解一般向量优化问题的主要目标法、线性加权和法和理想点法[5],分别提出求解向量多项式优化问题的主要目标法、线性加权和法和理想点法.这些方法的总体思路是将多目标函数转化为单目标函数,从而得到一个多项式优化问题,再利用Lasserre松弛方法求解该问题.
2.1 向量多项式优化问题的主要目标法
假定要同时考察k个目标f1(x),…,fk(x),其中变量x∈K,由(2)式所定义.在不考虑其他目标时,记第i个目标的最优值
(8)
相应的最优解记为xi*(i=1,2,…,k).
假设f1(x)为主要目标,而对其他k-1个目标fi(x)(i=2,…,k)有一组允许的界限值,即希望满足以下条件:
fi(x)≤fi(xi*)+aii=2,…,k,
(9)
其中ai为取定的合适常数.通过添加额外的约束条件,问题(3)转化成如下多项式优化问题:
(10)

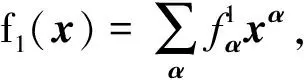

(11)
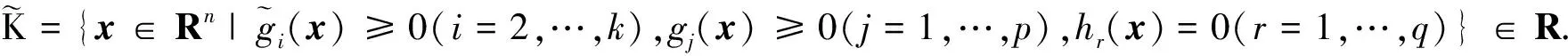
基于Lasserre松弛方法求解向量多项式优化问题的主要目标法的步骤如下:
(ⅰ)对于给定的原向量多项式优化问题(3),确定f1(x)为主要目标,则当f1(x)取得最小时,其他k-1个目标需满足条件(9);
(ⅱ)对所有的i=2,…,k,求解问题(8),求出对应的xi*;
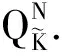
现证明用以上主要目标法求得的解是原向量多项式优化问题(3)的弱有效解.
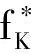
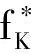

下面对向量多项式优化问题的主要目标法进行数值实验.数值实验的运行环境是:操作系统为Win10的8GB RAM的计算机,处理器为Intel i5-6500 dual core@3.20 Hz,调用Matlab R2016b软件,求解单目标多项式优化问题的软件包为GloptiPoly 3[17](这个软件包的核心算法是基于Lasserre松弛方法).线性加权和法和理想点法的数值实验运行环境与此相同.
算例1考虑向量多项式优化问题:
0≤x1≤2,0≤x2≤3.
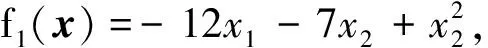
0≤x1≤2,0≤x2≤3.
用Lasserre松弛方法求解上述问题,得到最优值约为-16.667 5,x*≈(0.669 6,1.598 0),对应目标函数值(f1(x*),f2(x*))≈(-16.667 5,-5.847 2).由定理3可知,x*也为原向量多项式优化问题的弱有效解.
算例2考虑向量多项式优化问题:
0≤x1≤3,0≤x2≤4.
该问题中的约束条件取自文献[17].假设其主要目标函数为f1(x)=-x1-x2,则当f1(x)取得最小时,目标函数f2(x)要满足条件(9).这里设置ai=|fi(xi*)/10|,对于i=2,求解对应问题(10),即
minf1(x)=-x1-x2,
0≤x1≤3,0≤x2≤4.
用Lasserre松弛方法求解上述问题,得到最优值约为-4.053 7,x*≈(0.611 6,3.442 1),对应目标函数值(f1(x*),f2(x*))≈(-4.053 7,-3.212 2).由定理3可知,x*也为原向量多项式优化问题的弱有效解.
算例3考虑向量多项式优化问题:
x1+x2+x3≤4,3x2+x3≤6,0≤x1≤2,x2≥0,0≤x3≤3.
该问题中的约束条件取自文献[18].假设其主要目标函数为f1(x)=-2x1+x2-x3,则当f1(x)取得最小时,目标函数f2(x)要满足条件(9).这里设置ai=|fi(xi*)/3|,对于i=2,求解对应问题(10),即
minf1(x)=-2x1+x2-x3,
x1+x2+x3≤4,
3x2+x3≤6,
0≤x1≤2,x2≥0,0≤x3≤3,
用Lasserre松弛方法求解上述问题,得到最优值约为-3.530 3,x*≈(2.000 0,0.874 3,0.404 6),目标函数值(f1(x*),f2(x*))≈(-3.530 3,-9.333 4).由定理3可知,x*也为原向量多项式优化问题的弱有效解.
2.2 向量多项式优化问题的线性加权和法

(12)

(13)
其中:c为任意常数(c≠0);
(14)
(15)
s.t.MN(y)0,

基于Lasserre松弛方法求解向量多项式优化问题的线性加权和法的步骤如下:
(ⅰ)对于给定的向量多项式优化问题(3),利用α-法确定一组权系数λi(i=1,2,…,k);
(ⅱ)做出新的目标函数
(16)
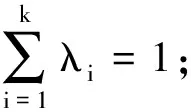
(ⅲ)将原向量多项式优化问题(3)转化成单目标多项式问题(16),用Lasserre松弛方法求解问题(16)的全局最优解.
现证明用以上线性加权和法求得的解是原向量多项式优化问题(3)的弱有效解.
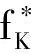
证明过程与定理3类似,在此省略.
下面对向量多项式优化问题的线性加权和法进行数值实验.
算例4考虑向量多项式优化问题:
0≤x1≤2,0≤x2≤3.
该问题中的约束条件取自文献[19].记约束集合
在约束集合K下,利用(14)式对目标函数分别求得其最优解为:
算例5考虑向量多项式优化问题:
0≤x1≤3,0≤x2≤4.
该问题中的约束条件取自文献[17].记约束集合
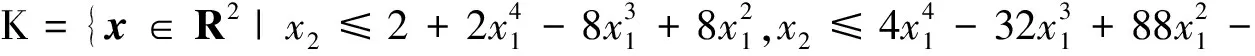
在约束集合K下,利用(14)式对目标函数分别求得其最优解为:
算例6考虑向量多项式优化问题:
该问题中的约束条件取自文献[19].记约束集合为
K={x∈R5|20x1+12x2+11x3+7x4+4x5≤40,0≤x1,x2,x3,x4,x5≤1}.
在约束集合K下,利用(14)式对目标函数分别求得其最优解为:
2.3 向量多项式优化问题的理想点法

对于不同的模,可找到不同意义下的最优点,一般定义的p-模为

(17)
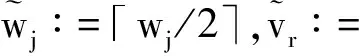
s.t.MN(y)0,
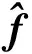
基于Lasserre松弛方法求解向量多项式优化问题的理想点法的步骤如下:
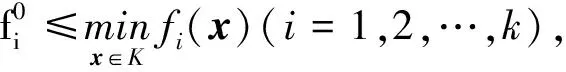
(ⅱ)构造新的目标函数(17);

下面证明用以上理想点法求得的解是原向量多项式优化问题(3)的有效解.
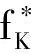
证明过程与定理3类似,在此省略.
下面对求解向量多项式优化问题的理想点法进行数值实验(为了避免罗列太多结果,此处令p=1或p=2).
算例7考虑向量多项式优化问题:
0≤x1≤2,0≤x2≤3.
该问题中的约束条件取自文献[19].分别对单目标f1(x),f2(x),f3(x)求得其最优解,对应的目标值为:


算例8考虑向量多项式优化问题:
0≤x1≤3,0≤x2≤4.
该问题中的约束条件取自文献[17].分别对单目标f1(x),f2(x)求得其最优解,对应的目标值为:


3 结语
结合求解一般向量优化问题的方法和Lasserre松弛方法,提出了求解向量多项式优化问题的主要目标法、线性加权和法和理想点法.数值实验结果表明这些方法都是有效的,都能得到原向量多项式优化问题的弱有效解或有效解.
