计及供电成本的小水电群经济调度优化模型研究
2019-04-14杨培文
夏 军,叶 超,魏 洁,姜 鹏,董 军,杨培文
(1.国网四川省电力公司雅安供电公司,四川 雅安 625000;2.北京中恒博瑞数字电力科技有限公司,北京 100085;3.能源市场研究所(华北电力大学),北京 102206)
水资源作为一种可再生的清洁能源发电,相比火力发电以及核电等方式更加绿色环保。四川省是我国水资源贮藏大省,加上各小流域水电蕴藏量,蕴藏量可达1.64亿千瓦左右,居全国第二位。雅安地处成都平原向青藏高原过渡地带,相对高差较大,境内降水量充沛,2016年底雅安电网调度管理并网水电厂643座、发电机组1 315台、水力发电总装机185.117万千瓦,装机占比达99.92%。但雅安电网水电装机占比较高,如何有效消纳大规模水电己经成为雅安地方政府和电网公司亟待解决的问题。
由于江河来水周期性和季节性较强,水电调节性能总体较差,多年调节性能的水电站仅占21%,导致水电群出力在年内分布极不均匀,丰枯期出力悬殊,枯期平均出力仅为丰期平均出力的三分之一。除此之外,雅安当地并网的小水电站几乎都是径流式小水电,多在山区或离城市较远的地区,具有规模小、设施老旧等特点,在现阶段运行时,还存在两个较为紧迫问题尚待解决,即过电压安全问题和雅安地区电价倒挂现象。
为了提高雅安小水电本地就近消纳,减少上网电量,合理规避价格倒挂等问题,将上述问题看作是小水电站群的经济性优化调度问题。国内外学者提出了许多解决方法,如传统规划算法[1-2]和智能算法[3-4]两大类。文献[5]梯级小水电群中各水库的发电引用流量作为决策变量,建立以发电量最大的梯级小水电群优化调度模型;文献[6]考虑了机电和涡轮发电机的能量损失,将水电机组排程调度问题建模为一个非线性混合的0—1规划问题,采用对偶分解的两阶段方法解决此问题;文献[7]在保证大坝安全的前提下,以梯级电站在调度周期内发电量最大为目标,采用浮点数编码的遗传算法进行求解;文献[8]考虑大小水电系统运行的经济性和可靠性,考虑约束容忍度的改进粒子群优化算法求解协调调度优化模型;文献[9-10]提出了大小水电可消纳电量期望值最大短期协调优化调度模型,并应用启发式搜索和关联搜索方法进行求解。
综上所述,本文以丰水期小水电富集的雅安地区为背景,针对雅安当地小水电站老旧设备的高故障率导致的高维修费和买卖电价格倒挂等问题,提出了小水电就地消纳和提出了满足当地负荷需求的建议。同时,考虑各个小水电站故障成本及折旧成本分摊,在满足雅安地区负荷需求的基础上,以地区供电总成本最小为目标,实现雅安当地小水电站的经济调度。此外,本文选择改进遗传算法来解决上述优化调度问题。
1 基本原理
1.1 改进遗传算法
遗传算法(GA)是一种模拟达尔文自然选择和遗传机制。对于大规模小水电系统,由于电站数量多,在此问题中每个电站又分为24个时段。同时,每个时段每个电站又对应一个开停机的状态变量,变量规模庞大,导致解空间随变量的增加而急剧增长,求解时间大幅增加,计算效率难以满足实际工程要求。因此,为了避免早熟,过早收敛导致产生局部最优解现象的发生,本文采用自适应模拟退火遗传算法。
1.1.1自适应处理
首先算法具备较强的鲁棒性和更高的计算效率,采用自适应函数来调整改良变异算子和交叉算子,即
(1)
(2)
式中,fm为要进行交叉处理的两个个体中适应度较大值;favg为每代群体的平均适应度值;fmax为群体中最大的适应度值;f为要变异个体适应度值。其中pc1、pc2、pm1、pm2均为常数。
1.1.2模拟退火遗传算法原理
该算法以增加种群多样性为目的,在初始化状态下种群足够丰富和算法依旧保持种群多样性特点,具体流程如图1。

图1 自适应模拟退火遗传算法操作流程
具体步骤如下:
(1)初始化参数,参数包括种群规模M,进化代数G,交叉概率Pc,变异概率Pm。
(2)初始化种群1,2,3,计算种群中各个个体的适应度值f。
(3)进行选择、交叉、变异操作,生成子代个体,计算子代个体的适应度f。
(4)判断是否满足接受函数,若是,接受新个体,否则以一定概率接受新个体。
(5)对新个体进行降温操作。
(6)判断值是否满足预期函数值,若是,输出最优解,否则转到第3步。
在算法运行过程中,初始参数选择尤为重要,其中Pc和Pm通过自适应函数求解。本文采用的算法包含外循环和内循环两种模式,即外循环为遗传算法,控制着最优解的决定权;内循环为模拟退火算法,主要控制降温操作,以跳出局部最优解,从而具有更大可能性去获取全局最优解。
1.2 成本分摊计量
由于某些小水电站的设备老化严重,故障率较高,因此针对该类小水电站的折旧成本及维修成本按其发电量分摊计量,来判定该类水电站发电的经济性。
1.2.1折旧成本分摊计量
水电机组n的单位电量折旧费用为Cdn,水电机组n总投资为In,使用寿命周期为Y,机组n残值为In′,水电机组n的年均发电量为Qn,则其按电量分摊的折旧成本为
(3)
1.2.2故障维修成本分摊计量
水电机组n的单位电量故障维修成本分摊为Cmn,则其计算表达式为
(4)
式中,C0为单次工人维修费用;PnλToff为机组n因维修停止发电运作而损失的利益;其中Pn为机组n的装机容量;λ为销售电价;Toff为机组停止运作的时间;a为机组n年故障维修次数。
2 小水电站经济调度优化模型
由于雅安当地发电电源几乎全部为小水电站,呈混联分布,且有部分水电站之间也存在上下游水量联系,因此模型的搭建需考虑上游电站水量对下游电站的影响,在建立水量平衡关系式时,需根据有无调节能力将小水电站分为两类。最后以雅安地区系统供电成本最小为目标搭建经济调度优化模型,即

Ui,t-1(1-Ui,t)CDi,t]+ptΔPt}
(5)
Chi=Cdi+Cmi
(6)
Phi,t=Ai×qi,t×hi,t
(7)
(8)
式中,Chi表示第i个水电站的单位发电量固定成本分摊;Cdi表示第i个水电站的单位发电量折旧分摊;Cmi表示第i个水电站的单位发电量故障维修成本分摊;Phi,t表示第i个水电站t时段的出力;Ai表示第i个水电站的出力转换系数;qi,t表示第i个水电站t时段的发电引用流量;hi,t表示第i个水电站t时段的平均水头;Ui,t表示第i个水电站t时段的开停机状态,0表示开机,1表示停机;CUi,t和CDi,t分别为启停机成本;pt为t时段电价,Pt为t时段需求侧负荷功率;M为水电站的总数量。
约束条件具体如下:
(1)库容约束
vi,min≤vi,t≤vi,max0
(9)
(2)发电引用流量约束
qi,min≤qi,t≤qi,max
(10)
(3)水量平衡约束。针对水量平衡约束,分为有水库有调节能力的水电站水量平衡公式
vi+1,t+1=vi+1,t+(ni+1,t-Qi+1,t+Qi,t)Δt
(11)
无水库径流式小水电站水量平衡公式
ni+1,t+Qi,t=Qi+1,t
(12)
(4)功率平衡约束
(13)
(5)下泄流量约束
Qi,min≤Qi,t≤Qi,max
(14)
(6)水电站出力约束
Phi,min≤Phi,t≤Phi,max
(15)
(7)机组最小运行时间约束
(Ui,t-Ui,t-1)+(Ui,t+v-1-Ui,t+v)≤1,
t∈1,2,…,(T-v);v∈1,2,…,(Ton-1)
(16)
(8)机组最小关停时间约束
(Ui,t-1-Ui,t)+(Ui,t+v-Ui,t+v-1)≤1,
t∈1,2,…,(T-v);v∈1,2,…,(Toff-1)
(17)
(9)末水位控制约束
(18)
3 算例
3.1 情景设置
雅安某区域小系统丰水期日前经济调度,发电机组全为水电机组,共计5个水电站,即H1、H2、H3、H4、H5,系统内部全天供电量大于系统用电需求量。其中,水电站H1、H2是拥有水库有日调节能力的两座可调节小水电站,其余水电站都为不可调节的径流式水电站,各水电站特征基础数据见表1。
此外,水电站H1和H2最小库容(死库容)分别为133.4万m3和383万m3,最大库容分别为1 575.1万m3和1 492万m3,水库正常水位分别为792 m和327 m,死水位分别为758 m和302 m。同时,水电站H3、H4和H5均是无水库。

表1 基础数据
在上述大背景下,本文设置两个情景:
(1)所有水电站满发,富余电量统一上网。由于处于丰水期,该区域所有水电站发电的供电量大于当地的负荷需求量,存在部分富余电量,该场景在满足当地负荷需求后,其余全部富余电量按照当地上网电价默认全部卖给四川省主网。
(2)水电站根据成本排序,以经济性为目标,在不同时刻以成本最低为原则,在满足总需求的基础上,同时与省主网有电量交互。当水电站的发电成本高于省主网购电价格时,该水电站会停止发电;若低于省主网购电价格,保持开机发电状态。
3.2 模拟仿真
该模拟仿真的计算条件如下所示:
(1)假设水电站的自然来水量均为确定的。
(2)设定为24时段日前调度,针对不同时段设置丰水期电价和峰谷平电价,其中高峰时段为7∶00~11∶00,19∶00~23∶00,低谷时段为23∶00到次日7∶00,平段为11∶00~19∶00。
(3)设定电价变动,销售侧丰枯电价具体变动为:在平水期丰水期电价下浮5%。峰谷分时浮动电价按高峰时段在丰枯浮动基础上上浮50%,低谷时段在丰枯浮动基础上下浮50%;上网侧取消峰谷电价,仅设置丰水期电价在平水期价格基础上下浮24%。按照此规则变动后的丰水期下网峰谷平电价分别为:0.567 15元/(kW·h),0.378 1元/(kW·h),0.189 05元/(kW·h);丰水期上网电价为0.08元/(kW·h)。
(4)雅安某区域小系统的第二天需求侧预测日负荷曲线如图2,看出存在3个尖峰,分别为早上6∶00~8∶00,中午11∶00~13∶00及晚上18∶00~20∶00 3个时段。

图2 雅安某区域日负荷曲线
(5)各水电站发电引用流量下限为0,上限为最大发电引用流量。
(6)改进遗传算法参数设置如下,种群数量n=50,最大进化迭代次数为g=100,pc1=0.8,pc2=0.5,pm1=0.1,pm2=0.01,初始温度T0=100,依照章节1.2中给出的算法步骤逐步降温到终止温度。
本模拟仿真运用Matlab软件实现,将设定好的参数代入所建模型的目标函数和约束条件中,再代入编写的程序算法中进行计算。考虑到遗传算法结果的不确定性,每次的运算结果都会有差异,本文对该模型进行10次模拟仿真,最终结果最终取10次仿真结果的平均值。各小水电站的出力情况如表2。如上图表,总结水电站优化调度结果,从开停机状态及出力情况展开分析。首先从机组开停机状态分析,水电站H1、H2、H324 h内都处于开机状态;水电站H4在9∶00~22∶00处于开机状态,其余时间段处于关机状态;水电站H5只在11∶00~13∶00和18∶00~20∶00两个时段开机,其余时段关机。再从出力水平分析,水电站H1、H2、H4开机时段内几乎都处于满发状态;水电站H3除0∶00~4∶00处于未满发状态,其余时段均处于满发状态;水电站H5开机时段都处于未满发状态。
出现上述调度优化结果,原因为各水电站单位电量的固定成本分摊不同。下表3为各水电站投资成本和运营成本的相关基础数据,根据1.2所述的成本分摊计量方法求得各小水电站单位电量固定成本分摊。
表1中,可看出各水电站单位电量的固定成本分摊H5>H4>H3>H2>H1,上述结果是由于各水电站设备老旧化程度不同造成的,水电站H3、H4、H5设备老旧化较为严重,在日常运行中,故障率较高,维修费用较高,导致单位发电量的折旧成本和故障维修成本分摊较高,其中水电站H5设备老旧化最为严重,其固定成本分摊最高。

表3 各水电站固定成本分摊

表4 情景总成本对比分析 元
为追求系统总成本最小,因电站H5单位电量的固定成本分摊在5个水电站中最高,该电站在谷时段和平时段发电成本高于上网电价,在电量富余的状态下,该电站的发电不经济,因此该电站只在两个峰时段发电,起到调峰作用,其余时段选择不发电;水电站H1、H2固定成本分摊最低,低于上网电价,作为基负荷24时段满发;水电站H3、H4相比H1、H2固定成本分摊较高,虽高于上网电价,但低于从省主网购电价格,因此可用来填补谷时段和平时段的负荷差,根据负荷需求安排机组出力,拟合负荷曲线。最后,针对系统运行总成本对比分析,其中场景2分别采用一般遗传算法和改进遗传算法求解,结果如表4。
可以看出丰水期调度优化前系统调度总成本(情景1)远高出考虑设备老旧化程度及其固定成本分摊等因素的优化调度总成本(情景2),在于不考虑设备老旧化程度及其固定成本分摊等因素,全时段满发,富余电量上网卖出这种调度决策行为不够经济,因其发电运行成本已高出上网电价,这部分富余电量只会造成额外成本。相比之下,情景2以水电站机组的固定成本分摊为根据,将各小水电站发电进行排序,成本低者先发电,成本较高者用来调峰或者不发电,该优化调度从系统供电成本最低出发,考虑机组发电的经济性问题,调度安排更为合理,系统供电总成本最小。
其次,改进遗传算法求得的最终供电总成本要低于传统遗传算法,在于传统遗传算法由于易过早收敛,导致早熟,最终求得的最优解仅为局部最优,并非全局最优,使出力总曲线与负荷需求曲线拟合程度较差,残余偏差负荷较大,如下图3a所示,导致最终电网电量的交互成本大幅升高。相较之下,由于改进遗传算法全局搜索能力强,在求解运行过程中,可接受当前不是最优解的概率存在,因而可跳出局部最优情况,达到寻求全局最优解的目标,如图3b所示,水电站总出力与日负荷曲线偏差较小,电力交互成本大大较低,进而降低了总成本,优化效果更明显。
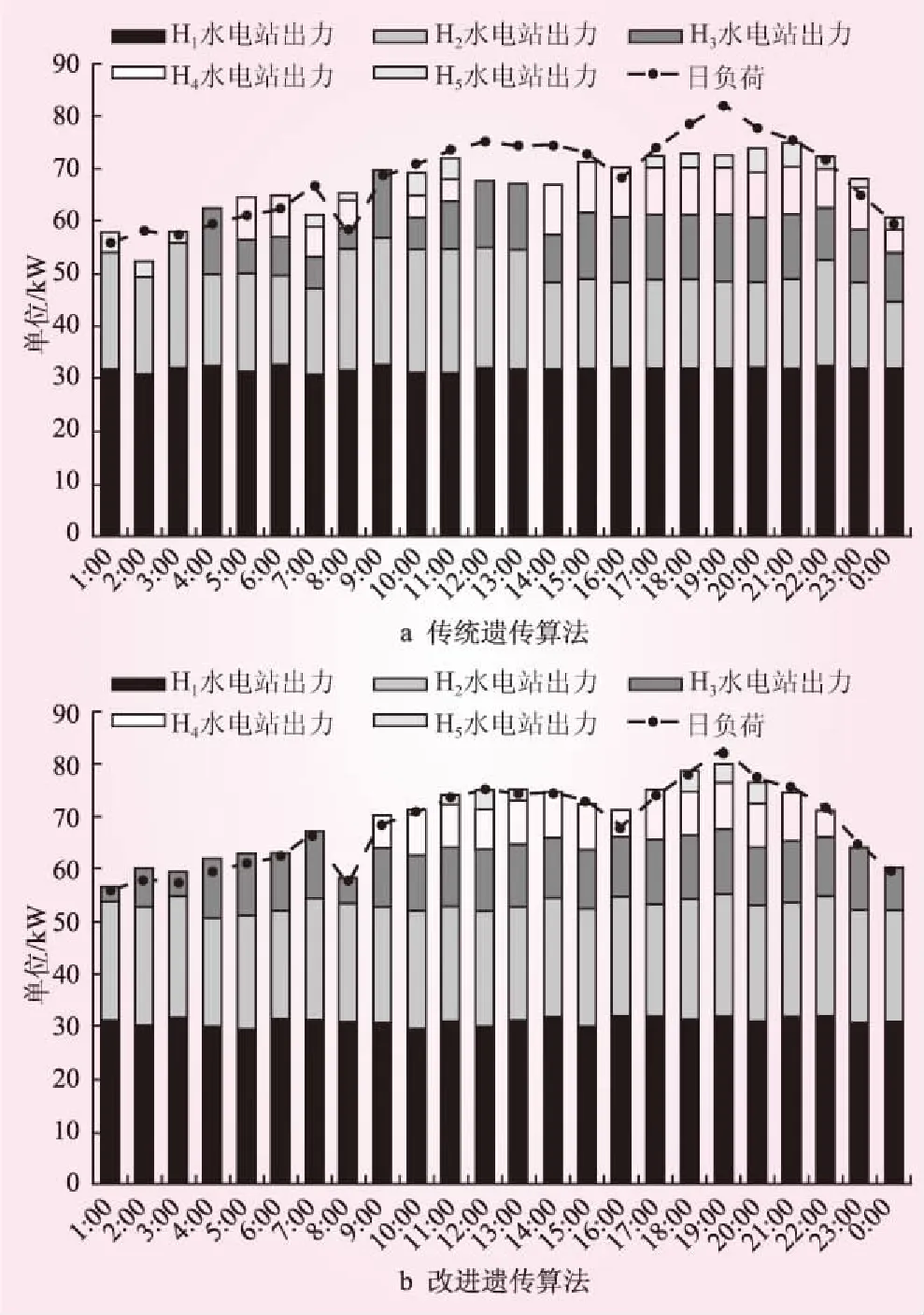
图3 传统遗传算法与改进遗传算法优化结果对比
4 结 论
(1)相比传统遗传算法,利用改进遗传算法求解多变量和多约束条件的非线性整数规划问题,全局搜索能力更强,避免了早熟现象的发生,使得计算结果更接近于全局最优解,优化效果更佳。
(2)同时从系统优化的整体性出发,考虑水电设备新旧程度,将年折旧成本和故障维修成本分摊到单位发电量中,再衡量判断水电站发电的经济性,最终指导雅安当地小水电群调度安排,将单位电量成本分摊较高水电站顶峰发电或者停机不发电。
(3)在一定程度上能够合理减少雅安当地小水电设备因老化严重,频繁发生过电压安全事故而带来高额的故障维修成本,同时规避了售电电价的价格倒挂等经济性问题,对降低雅安当地电力系统的供电成本,推动当地小水电产业的发展具有重要研究价值和意义。
