一种基于多阶段遗传算法的功率模块自动化布局方法

郝柏森，梅云辉，李 欣，陆国权



一种基于多阶段遗传算法的功率模块自动化布局方法

郝柏森1, 2，梅云辉1, 2，李 欣1, 2，陆国权1, 2

(1. 天津大学先进陶瓷与加工技术教育部重点实验室，天津 300350； 2. 天津大学材料科学与工程学院，天津 300350)

模块的布局设计是功率模块设计的关键环节，随着功率模块向着集成化、高频化飞速发展，布局设计对于模块可靠性的影响越来越重要．目前，功率模块的布局设计主要依赖于设计人员经验而以手工方法完成，在此过程中消耗了大量的人力和时间成本．电子设计自动化作为未来电子领域的发展趋势，近年来已经研究用于功率模块的设计之中．然而，传统遗传算法的应用造成自动化方法无法在可接受时间内得到准确的结果．针对该现状，设计开发了结果精度更高、运算速度更快的修正自动化布局遗传算法．该算法采用统计学、种群多阶段思想与遗传算法思想减少种群数量与运算复杂度，最终保证算法计算速度和精度的提高．将该算法用于简单的半桥模块实例的布局设计，并采用ANSYS Q3D软件验证，结果表明，相比于原来的自动化布局设计遗传算法，本文方法缩短了约29%的运行时间，并且布局方案的适应度平均值达到231.14，其标准差仅为0.43，优于原有方法175.35的适应度平均值和13.96的标准差．所以，本文方法可以在短时间内得到更准确的结果，这有助于将自动化方法真正用于实际功率模块的布局设计．

功率模块；自动化布局；多阶段遗传算法；寄生参数；低寄生电感

复杂多样化的应用场合不断对功率模块性能提出更高的要求[1]．目前，高效率与大功率是功率模块的发展方向，应用人员希望其在保证换流功能的基础上提高功率密度，功率器件工频的提高是最有效的途径．然而，随着工频的提高，d/d和d/d随之升高，在器件关断时，寄生参数会造成电压过冲与震荡，从而造成功率模块电气失效[2]．

作为材料的固有特性，寄生参数包括寄生电容、寄生电阻和寄生电感3项指标．功率模块的工频相对较低，寄生电容影响较小，并且可通过无源滤波方法补偿[3]．但是，对于减小模块的寄生电感和电阻，优化模块的布局是最经济，也是最有效的方法[4]．

目前，模块布局设计主要采用基于经验的手工设计．设计人员根据ANSYS Q3D软件对于布局进行建模仿真以确定该布局的性能[5-6]．如果模拟结果达不到预期，则还需重新设计，在此过程消耗了大量的时间和人力．另外，设计结果常常受到设计者经验的限制．对于更多器件的模块，由于排列方式的多样性，仅仅依靠人的经验和知识是远远不够的．因此，实现布局的自动化排布设计迫在眉睫．文献之中报道了多种半自动化布局算法，在限制器件方位之后再实现布局的优化，其结果仍然受到人为因素的影响[7-11]．Ning等[12]提出采用遗传算法思想自动设计模块的布局，然而问题在于如果模块并联芯片数量较多，带来的过大种群数量会造成遗传算法的早熟收敛，布局结果精度势必下降．

本文提出一种修正的多阶段遗传算法，可实现多芯片布局功率模块自动设计时，在保证布局结果精度的前提下，仍具有优异的计算效率．为验证本文提出算法的创新效果，本文采用与文献[12]相同的两芯片半桥模块设计案例，进行自动化低感布局设计．随后将各自计算获得的最优布局方案，通过ANSYS Q3D软件进行寄生参数提取与面积评估．

1 算法思路

文献[12]采用遗传算法来进行功率模块的布局设计．遗传算法遵循适者生存、优胜劣汰的原则，模仿自然界的选择与遗传机理，经过选择、交叉和变异更快算出最优解[13-14]．传统遗传算法流程如图1(a)所示，尽管算法可以通过变异生成新个体，然而到达一定程度之后，很难再以随机方式生成更优的新个体．因此，对于大规模种群数量的择优，其更容易早熟收敛[15-18]．正因如此，最终结果很大程度上取决于初代的选择．针对于遗传算法的缺点，笔者提出一种修正的多阶段遗传算法：将总体种群进行分段，通过减少每阶段遗传算法的种群数量，保证每一阶段结果的精度，提高大种群数量案例时候的最终结果精度．

如图1(b)所示，该方法将整个择优过程分成3阶段：

(1) 采用随机统计学方法设置准则，在原始总体种群之中筛选确定符合该准则的新种群，达到减小下一阶段种群数量的目的；

(2) 在新种群之中采用遗传算法筛选出适应度最高的个体，再依据此个体建立新准则；

(3) 最后重新在原始总体种群之中确定符合新准则的所有个体，再次进行遗传算法择优，获得适应度最佳的最终结果．

该方法一方面通过减少每阶段遗传过程的种群数量，保证每阶段的适应度结果精度；另一方面采用前一阶段所筛选得到的结果作为本阶段计算的初代条件，可显著提高本阶段计算的初代质量．因此，该方案可在提高结果精度的同时，也大幅提升其计算收敛速度．

图1 遗传算法流程

因此，本文提出的多阶段遗传算法具有运算高效、结果准确的理论可行性．

2 算法实施方案

2.1 适应度的定义

本文提出适应度的概念来评价模块布局方案的优劣．适应度充分考虑模块整体布局寄生电感、寄生电阻和衬底面积的综合作用，其定义为

 (1)

式中：parasitic为寄生电感，mH；parasitic为寄生电阻，W；footprint为衬底面积，mm2．

为了与文献[12]的方法直接比较，本文采用同样的寄生参数计算模型．寄生电感计算公式为

 (2)

 (3)

式中：为电流密度；0为真空磁导率；L为路径电感，mH．

寄生电阻评估采用的公式为

 (4)

式中：为导体的长度，mm；为导体的电阻率；为导体的横截面积，mm2；为连接路径寄生电阻，W．

2.2 位置信息表示方式

文献[12]采用序列对方法实现器件间位置的字符串表示．如图2(a)所示，2位字符串即可表示个器件的相互位置[19]，本文将此字符串定义为位置DNA．如图2(b)所示，器件的4个取向可以用4种两位字符(00，01，10，11)来表示．因此个器件的取向DNA的位数即为2．在本文中，间距被定义为器件的左下角到左或下边缘的距离.元器件之间的间距被设为0～7mm，分度值为1mm.将间距值用二进制字符表示，本文将此字符串定义为间距DNA，则每个间距值可以用3位字符代表．

因此，器件相互位置、器件取向和器件间距的DNA字符串组合应含10个字符，该字符串组可完全描述个器件的位置信息，将此字符串定义为外回路DNA．值得注意的是，如图2(d)所示，芯片、导线和芯片下面的铜导带被简化为一个功率单元，以节省整体算法的运行时间．

2.3 算法结构

采用第2.2节所述的器件位置表达方式，若针对5器件模块进行布局设计，其位置DNA、取向DNA和间距DNA的种群数分别为(5!)2、45和810．所以，三者相乘，该模块的整体DNA种群数量高达1.58×1016．为保证计算效率，算法应该避免过多的迭代次数．在这种情况下，如此庞大的种群数量势必造成遗传算法结果精度的下降．

图2 器件位置信息表示方式定义

根据第1节，初代质量与种群数量对于结果精度和程序运算时间影响显著．因此，本文采用多阶段分别筛选的思路，以获得最后阶段更优质量的初代为工作目标，大幅减少各阶段的种群数量，最终可以在保证计算效率的前提下，获得适应度更优的布局结果．

根据该理论，本文提出的多阶段遗传算法如图3所示．第1阶段确定最佳的间距DNA；第2阶段固定第1阶段得到的间距DNA，获取最佳的位置DNA；第3阶段固定第2阶段得到的位置DNA不变，通过再次筛选取向和间距DNA，确定包含第2阶段获得的最佳位置DNA和第3阶段的取向和间距DNA的最终优化布局．该方法通过前两阶段的筛选，提高了第3阶段的初代质量，减少了种群数量，最终必然实现更佳的结果精度．

图3 多阶段遗传算法计算流程

2.3.1 算法第1阶段

第1阶段可分为两个回路，其中外回路实现筛选获得最佳的间距DNA，内回路根据外回路生成的DNA形成电气连接，完成适应度评估．其具体操作如下：外回路随机生成100个位置DNA与取向DNA组合，分别固定所有器件之间的间距为1、2、3、4、5、6、7．在同样的位置与取向DNA条件下，经过内回路的适应度评估结果，比较间距对于适应度的影响，统计7种间距之中哪种的适应度最高，该阶段的外回路计算次数为700次，其具体过程如图4所示．

图4 多阶段遗传算法的具体DNA操作过程

当外回路生成DNA之后，内回路根据电路图逻辑来实现铜导带连接和适应度评估，将适应度值最大的铜导带连接方案以字符的形式保存下来，即定义为内回路DNA．其具体过程如下：首先基于外回路DNA生成标明器件位置的二维矩阵，随后根据电路图拓扑实现器件之间的线互连，线互连完成之后确定空白阵点的数目，将该数值乘以3/4或者4/5，作为铜导带覆盖的阵点数量，将该数量的铜导带阵点随机覆盖在空白位置，由此完成完整的布局方案．根据铜导带连接情况，采用第2.1节所述公式评估该布局的适应度．

由于该部分种群数量庞大，所以采用遗传算法．经过多次迭代优化铜导带连接，具有最佳适应度的铜导带连接方式被输出至外回路，外回路根据适应度值进行比较，得到最佳的间距DNA．

2.3.2 算法第2阶段

本阶段也可分为两个回路，其中外回路为得到最佳的位置DNA，内回路程序与第1阶段程序完全一致．其具体操作如下：首先固定第1阶段得到的最佳间距DNA，此时本阶段筛选的种群包含所有的位置DNA与取向DNA组合．以5器件模块为例，本阶段外回路种群数量变为1.47×107．在该低种群数量条件下，采用遗传算法对外回路的种群进行择优计算，可以得到更佳的位置DNA结果．

在该部分的遗传过程之中，由于后6位的间距DNA字符串是固定不变的，所以交叉点和变异点在外回路DNA的前4位范围内随机产生．如果交叉点在第2＋1位与4位之间，则该点及该点之前的字符串保持不变，该点后面的字符相互交换．如果变异点在第2＋1位与4位之间，则该点的字符由0变为1，或者由1变为0．图5(a)举例演示了该遗传过程，其交叉点与变异点分别为5与9．

若交叉点位于前2位，则采用通用拓扑保持交叉方法进行交叉[20]．在字符串中，首先找到两个母代的最长公共子序列．然后，序列中的字符以相同的顺序保存，其余非序列内的字符依次进行交换．其具体过程如图5(b)所示．该方法使两个母代的共同特征得以保留．若变异点位于前位，则在该范围内再生成一点，将两点位置的字符进行交换；若变异点位于第＋1位到2位，则在该范围内进行相同的操作．

图5 DNA遗传操作过程

2.3.3 算法第3阶段

第3阶段同样包括两个回路．其具体操作如下：首先外回路固定第1部分所得到的位置DNA不变，然后采用遗传算法得到最佳的取向和间距DNA，该结果即为最终的最佳布局结果．该部分的种群数量为1.10×1012．由于取向与间距DNA均由0与1组成，所以其交叉遗传方式与图5(a)一致，遗传过程相比第2阶段更简单，因此相比于文献[12]之中的算法，本算法的筛选速度得到显著提升．

综上，将700、1.47×107、1.10×1012三者相加，即得到新算法3个阶段种群数量总和约为1.10×1012，远低于文献[12]的算法的1.58×1016．因此，本文提出算法的最优布局结果精度与计算速度将得到显著提高．

3 自动化布局演示

文献[12]采用如图6所示的含有三端子、两开关半桥电路来验证本文算法．为了能够与文献[12]中的算法直接比较，本文采用多阶段遗传算法，针对相同的半桥电路进行自动化布局设计．其中半桥模块的材料属性如表1所示．

图6 自动化布局例子

表1 材料属性

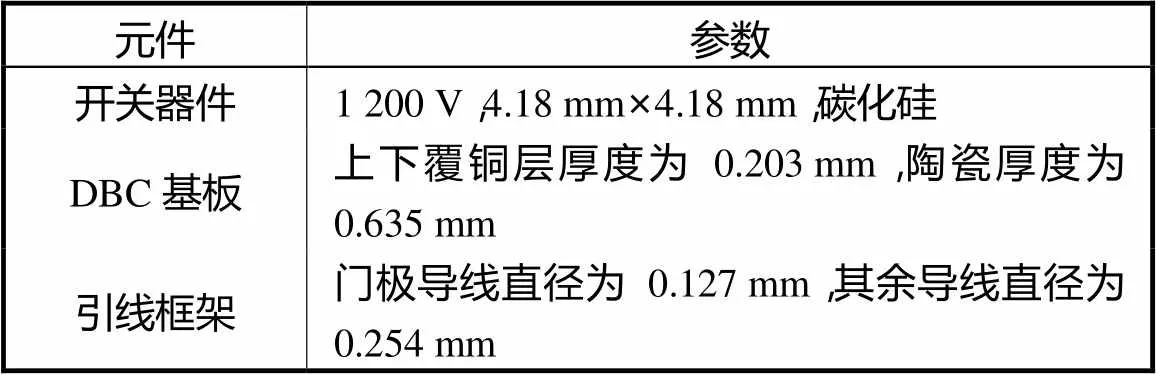
Tab.1 Material performance

3.1 遗传参数的确定

利用MATLAB，本文以图6所示半桥拓扑的模块为例，研究了各阶段参数对于最优布局的适应度结果的影响．

如图7所示，在第1、第2阶段的内回路之中，为了提高运行速度，假设基板的面积为mm，则初始种群的数量、交叉和突变次数全部选择为0.05即可．而在第3阶段的内回路之中，为了得到准确结果，初始种群的数量、交叉和突变次数全部选择为0.5．

在第2阶段的外回路中，若器件个数为，为保证计算精度，初代个数与交叉变异次数均设置为6．而在第3阶段，由于该阶段种群数量更庞大，初代个数与交叉变异的次数均设置为8．经过实测，在以上的参数设定条件下，本文可以用最短的时间，得到鲁棒性达到100%的结果．

图7 内外回路参数对于结果的影响

3.2 布局结果验证

本节对于本文方法与文献[12]方法的布局方案进行对比．

由于含有5个器件，本文方法在第2阶段经过30次外回路迭代，在第3阶段经过40次外回路迭代算法停止．为了直接比较运算效率，同样经过40次外回路迭代，文献[12]的算法停止．两种方法均重复运行20次以验证鲁棒性．两种算法最优布局的适应度结果与运行时间如图8所示．通过多阶段遗传算法，遗传算法的优化速度显著加快．相比于文献[12]之中的算法，本文算法运行时间减少了约29%．多阶段遗传算法的适应度结果平均值高达231.14，其标准差仅为0.43，所以其结果适应度以及鲁棒性均优于文献[12]的遗传算法．

文献[12]方法以及本文的多阶段遗传算法所获得的最优布局分别如图9(a)和图10所示．利用ANSYS Q3D，本节对布局方案进行比较．文献[12]所提出方法获得的最优布局的适应度仅为157.1．如果固定其外回路DNA中的位置DNA，仍采用遗传算法进行迭代，所获得的最优布局如图9(b)所示．该布局的适应度则增加至162.6，所以文献[12]算法提出的最优结果只是局部最优．而根据本文提出的多阶段遗传算法获得的最优布局的适应度高达228.3．综上，相比于文献[12]，本文提出的多阶段遗传算法可以更高效、准确地实现功率模块的自动化布局．

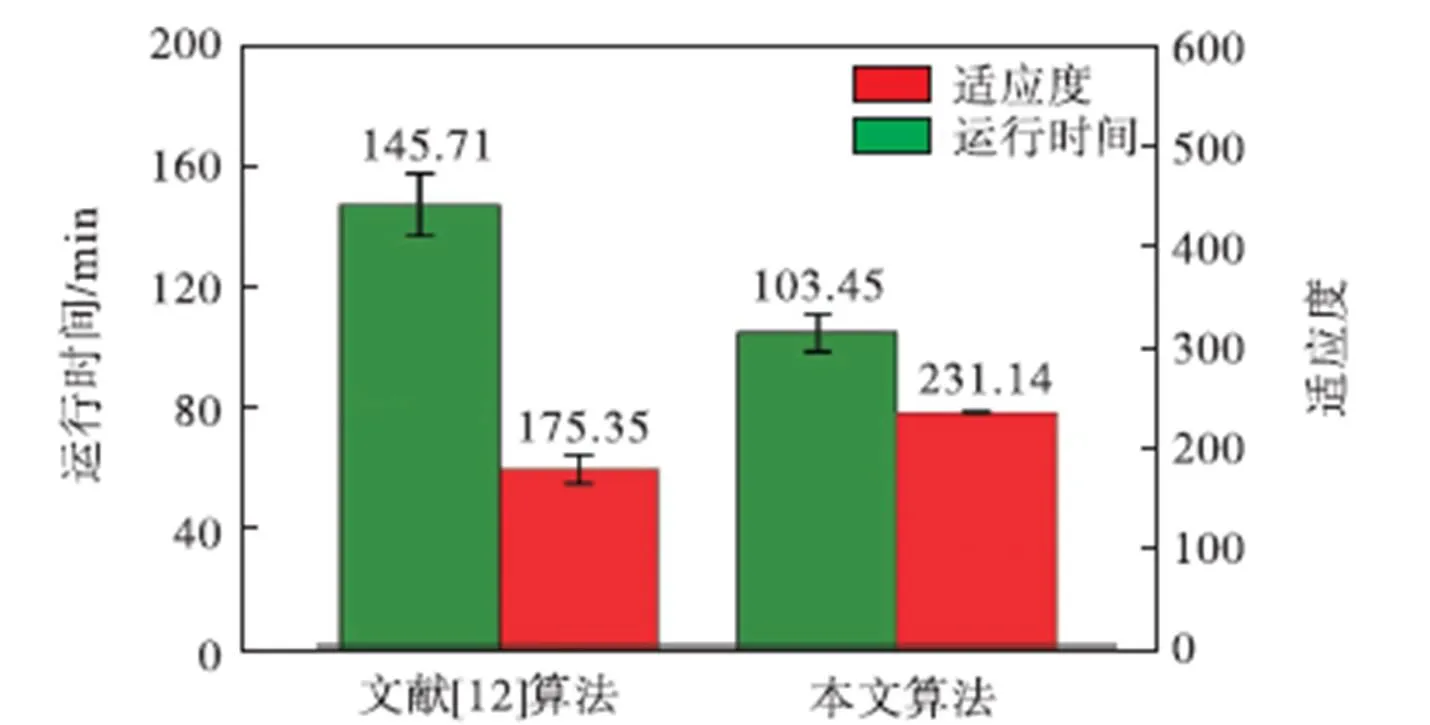
图8 不同自动布局算法的适应度值与运行时间对比

图9 自动化设计布局

图10 本文提出方法获得最优结果

表2 不同布局方式的参数对比

Tab.2 Comparison of parameters for different layouts

4 结 语

本文提出了一种快速、准确的功率模块自动布局方法．通过统计学与多阶段遗传算法思想结合，减少每阶段遗传算法的种群数量．该方法减少算法的运行时间的同时，结果的准确性和鲁棒性得到显著提高．通过设计实例验证，该自动布局算法得到的布局结果远远优于文献[12]的算法，并且计算时间减少了29%．该自动化布局方法对今后实现科学有效地提高功率模块的性能具有重要意义．

［1］ 陆国权，李 洁，梅云辉，等. 大功率IGBT模块瞬态热阻的测试方法与装置[J]. 天津大学学报：自然科学与工程技术版，2017，50(7)：669-675.

Lu Guoquan，Li Jie，Mei Yunhui，et al. Measurement method and device for transient thermal impedance of high power IGBT module[J]. Journal of Tianjin University：Science and Technology，2017，50(7)：669-675(in Chinese).

［2］ Kim Y J，Nakaoka M，Takano H，et al. Comparative performance evaluations of high-voltage transformer parasitic parameter resonant inverter-linked high-power DC-DC converter with phase-shifted PWM scheme[C]// Power Electronics Specialists Conferencea，IEEE. Atlanta，GA，USA，1995：120-127.

［3］ Wakimoto T，Akazawa Y. A low-power wide-band amplifier using a new parasitic capacitance compensation technique[J]. IEEE Journal of Solid-State Circuits，1990，25(1)：200-206.

［4］ Mustain H A，Lostetter A B，Brown W D. Evaluation of gold and aluminum wire bond performance for high temperature(500℃)silicon carbide(SiC)power mod-ules[C]// Electronic Components and Technology Conference，IEEE. Lake Buena Vista，FL，USA，2005：1623-1628.

［5］ Hao B，Mei Y，Ning P. A hybrid genetic algorithm for automatic layout design of power module[C]// International Conference on Electronic Packaging Technology，IEEE. Harbin，China，2017：1143-1146.

［6］ Fu S，Mei Y，Li X，et al. Reliability evaluation of multichip phase-leg IGBT modules using pressureless sintering of nanosilver paste by power cycling tests[J]. IEEE Transactions on Power Electronics，2017，32(8)：6049-6058.

［7］ Hingora N，Liu X，Mcpherson B，et al. Concerning layout synthesis for power electronic multi-chip modules[C]// IEEE Workshop on Control and Modeling for Power Electronics，IEEE. Boulder，CO，USA，2010：1-5.

［8］ Hingora N S，Liu X，Feng Y，et al. Power-CAD：A novel methodology for design，analysis and optimization of power electronic module layouts[C]// Energy Conversion Congress and Exposition，IEEE. Atlanta，GA，USA，2010：2692-2699.

［9］ Shook B W，Nizam A，Gong Z，et al. Multi-objective layout optimization for multi-chip power modules considering electrical parasitics and thermal performance[C]// IEEE Workshop on Control and Modeling for Power Electronics，IEEE. Salt Lake City，UT，USA，2013：1-4.

［10］ Chen J Z，Pang Y F，Boroyevich D，et al. Electrical and thermal layout design considerations for integrated power electronics modules[C]// Conference Record of the Industry Applications Conference，IEEE. Pitts-burgh，PA，USA，2002：242-246.

［11］ Martin C，Guichon J，Schanen J，et al. Gate circuit layout optimization of power module regarding transient current imbalance[J]. IEEE Transactions on Power Electronics，2006，21(5)：1176-1184.

［12］ Ning P，Wang F，Ngo K D T. Automatic layout design for power module[J]. IEEE Transactions on Power Electronics，2013，28(1)：481-487.

［13］ Goldberg D E. Genetic algorithm in search optimization and machine learning[J]. Addison Wesley，1989，ⅩⅢ(7)：2104-2116.

［14］ 刘恒丽，董靖川，于治强. 基于Pareto遗传算法和TRIZ理论的数控装备加工参数智能优化[J]. 天津大学学报：自然科学与工程技术版，2017，50(2)：121-127.

Liu Hengli，Dong Jingchuan，Yu Zhiqiang. Intelligent optimization of CNC equipment machining parameters based on pareto genetic algorithm and TRIZ theory[J]. Journal of Tianjin University：Science and Technology，2017，50(2)：121-127(in Chinese).

［15］ Deb K，Pratap A，Agarwal S，et al. A fast and elitist multiobjective genetic algorithm：NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation，2002，6(2)：182-197.

［16］ Li H，Zhang Q. Multiobjective optimization problems with complicated Pareto sets，MOEA/D and NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation，2009，13(2)：284-302.

［17］ Deb K，Agrawal S，Pratap A，et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization：NSGA-Ⅱ[J]. Lectures Notes in Computer Science，2000，1917：849-858.

［18］ Yang J，Honavar V. Feature subset selection using a genetic algorithm[J]. IEEE Intelligent Systems & Their Applications，2002，13(2)：44-49.

［19］ Murata H，Kuh E S. Sequence-pair based placement method for hard/soft/pre-placed modules[C]// International Symposium on Physical Design，ACM. Mon-terey，CA，USA，1998：167-172.

［20］ Hatta K，Wakabayashi S，Koide T. Solving the rectangular packing problem by an adaptive GA based on sequence-pair[C]// Proceedings of the Asia and South Pacific Design Automation Conference，IEEE. Hong Kong，China，1999：181-184.

An Automated Layout Design Method Based on Multistage Genetic Algorithm

Hao Baisen1, 2，Mei Yunhui1, 2，Li Xin1, 2，Lu Guoquan1, 2

(1. Key Laboratory of Advanced Ceramics and Machining Technology of Ministry of Education，Tianjin University，Tianjin 300350，China； 2. School of Materials Science and Engineering，Tianjin University，Tianjin 300350，China)

Floorplanning is one of the critical steps in designing a power module. With the rapid development of power modules toward high integration and frequency，floorplanning is becoming increasingly significant in ensuring reliability of power modules. Presently，the layout of a power module is mainly designed manually based on the designer’s experience，which is labor-and time-consuming，whereas，electronic design automation，as a development trend in the field of electronics，has been studied in recent years for the design of power modules. However，the application of traditional genetic algorithm cannot realize accurate layout results in a short time. To increase the calculation accuracy and speed，a modified genetic algorithm was developed in this study. By applying the concepts of statistics，multi-stage population，and genetic algorithm in the modified genetic algorithm，the population and complexity of operations were significantly reduced，which resulted in higher calculation accuracy and speed. Then this method was used for layout design of a simple half-bridge module and verified by ANSYS Q3D software. Compared with the traditional genetic algorithm，the modified genetic algorithm method saves calculation time by about 29%. Additionally，average fitness was increased from 175.35 to 231.14，and the standard deviation was reduced from 13.96 to 0.43. Therefore，the proposed modified genetic algorithm method can realize more accurate results within a short time，and this will contribute in making automated layout designs for power modules practicable.

power module；automated layout design；multistage genetic algorithm；parasitic parameters；low parasitic inductance

10.11784/tdxbz201808036

TN302

A

0493-2137(2019)06-0601-07

2018-08-09；

2018-11-28.

郝柏森（1993—），男，硕士研究生，haobaisen@163.com.

梅云辉，yunhui@tju.edu.cn.

国家重点研发计划资助项目(2016YFB0100600)；科学挑战计划资助项目(TZ2018003)；天津市自然科学基金资助项目(17JCYBJC19200)．

the National Key Research and Development Program of China(No.2016YFB0100600)，the Science Challenge Project (No.TZ2018003)，the Natural Science Foundation of Tianjin，China(No.17JCYBJC19200).

(责任编辑：孙立华)