状态序列的统计分析方法及其应用

王殿玺

(中国政法大学 博士后流动站，北京 100088)

一、引言

对于时间序列的分析，统计学已经有较为成熟的方法应对。时间序列是随时间顺序出现或采集的一连串观测数列[1]，而时间序列分析(Time Series Analysis)包括时域分析和频域分析[2]，是一种动态数据处理的统计方法，研究随机数据序列所遵从的统计规律[3]。换言之，时间序列是对随时间变化的动态数字序列统计规律的分析，但是除了时间序列，社会统计分析中还存在一种状态序列，比如个体角色状态序列，而对这种随时间或年龄变化的状态序列的统计分析和挖掘已得到不断关注，如可视化不同就业状态(无业、兼职就业、失业、培训、全职就业)序列的变化形态与特征等。当前，国外已经开始发展针对状态序列的统计分析技术，经过众多学者的不断改进和完善，状态序列轨迹的统计技术已经较为成熟，称之为序列分析方法(Sequence Analysis Method)，该方法已被应用于统计学、人口学、社会学以及老年学等学科领域，研究议题涉及就业状态变化、家庭-工作状态转换、婚育状态变换、健康失能轨迹以及人口迁移轨迹分析等。本文主要介绍序列分析方法的发展历程、数据类型要求以及实现步骤与功能，并试图通过案例的形式来阐释序列分析方法的应用价值。

二、序列分析方法的起源与发展

20世纪80年代，芝加哥大学教授阿伯特(Abbott)根据生物学领域的基因序列匹配技术和方法，将序列匹配的思想从生物科学领域引入到社会科学研究中，基因匹配的技术和方法主要是通过对不同基因序列进行匹配以分析基因链条的相似与差异，阿伯特借此思想提出了序列分析方法。序列分析方法在引入社会科学研究的初期，并没有得到学术界的广泛重视和应用，后来经过多位学者的不断改进，序列分析才重新引起了研究者的关注，特别是在生命历程研究领域，成为分析以事件为分隔的状态序列轨迹的重要工具。

综合而言，序列分析方法的发展和成熟大致经历了两个阶段：第一阶段为序列分析方法的初创期，主要以阿伯特为代表，其在20世纪80年代中期至90年代初发表了多篇论文介绍序列分析方法，阿伯特在综述社会学、心理学、政治学等学科对序列研究的基础上，论证了传统事件史分析方法在状态序列研究中的不足以及序列分析的优势[4]，序列分析方法在这一阶段最重要的发展在于最优匹配技术(Optimal Matching)的运用[5]，最优匹配技术是序列分析方法的核心，其能够实现以一定的转换成本计算状态序列之间的距离，从而解决了序列差异测度和转换的关键问题。但是由于最优匹配需要主观设定序列转换的成本，因而也受到了一些学者的批评和对结果有效性的质疑[6]。第二阶段，学者们致力于改进序列分析方法的不足，诸如基于数据转换率的成本设定方法的创立以及Dynamic Hamming等距离算法的引入[7-8]，显著优化了序列轨迹距离的计算方法；子序列度量和序列轨迹复杂性测量指数方法的发展[9]以及状态序列差异分析的建立[10]，使状态轨迹的测量方法更加完善；与聚类分析方法以及其他统计分析方法的结合，进一步扩展了序列分析方法的适用空间；Gabadinho等专门编写了序列分析统计软件包[11]，研究者可以方便地在R软件、STATA统计软件中操作和实现，这些都标志着序列分析方法的逐渐成熟。

三、序列分析的数据收集方法与形式

序列分析具有特定的数据收集方法及形式要求，在理想情况下，生命史日历(Life History Calendar，LHC)数据最适宜运用序列分析方法进行相关研究，尽管生命史日历在表面上是一个数据文件，但其实质上是合并了许多不同事件(如生育、结婚、迁移事件等)的表格，旨在收集关于事件的发生时间和顺序的数据[12]。生命史日历数据最大的优点在于能够使研究者在多个不同的关联领域中交叉核对事件的发生时间。生命史日历格式通常是一个大的矩阵表格，矩阵的一个维度详细描述了受访者的行为模式，如结婚、入学、就业等，而另一个维度则记录上述行为模式的时间单位，如什么时间结婚、入学、就业等，而调查人员正是根据受访者所提供的资料填写在对应的矩阵单元格上，借助受访者的上述历史资料信息，研究者可以较容易的记录个体在不同时间单位的角色状态并可以形成连续时间的状态序列轨迹。除了生命史日历方法之外，回顾性调查数据(Retrospective Life History Data)、纵向追踪数据(Longitudinal Data)、人口登记数据(Population Registration Data)也可以根据相关回顾性问题或历史登记信息构建受访者的状态序列轨迹，但是如果使用回顾性调查、纵向数据和人口登记的原始数据，需要将调查与登记的历史信息转换为可供序列分析的数据形式。此外，收集状态序列数据和构建状态序列还涉及到时间单位的选择与测量，通常会选择月或年作为时间单位，过宽或过于粗糙的时间单位均不合适，而同时收集受访者的人口学特征、家庭背景和社会经济地位变量也是较为理想的，可以进行更为深入的分析。

如上所述，根据生命史日历数据或回顾性调查数据，可以抽离出了个体在不同时间单位的特定状态，进而形成可以用于序列分析的特定状态序列。为了形成状态序列，首先要根据所研究的问题定义不同状态，而定义状态空间是应用序列分析方法的基础。例如，如果要研究家庭形式的变化轨迹，可以用婚姻、生育等方面的联合状态作为状态空间，并以此来构建应用于序列分析的家庭形式变化的状态轨迹，即在婚姻方面定义未婚、同居、已婚、离婚与丧偶5个状态，在生育方面定义无子女、有一个子女、有两个子女、有三个及以上子女4个状态，而将婚姻(5个状态)、生育(4个状态)领域的状态进行组合，则可形成20个家庭形式变化的联合状态(5个婚姻状态×4个生育状态)，如单身且无子女状态、已婚且有3个及以上子女状态等。状态有两种代表方法，一种是用不同的字母代表序列的不同状态，一种是用不同的数字代表序列的不同状态。例如，可以用SNC代表单身且无子女状态，也可以用1代表单身且无子女状态。基于上述联合状态，可以构建每个个体家庭形式变化的状态序列，表1即以年为单位呈现的状态序列，表中每一个序列代表着一个个体家庭形式变化的状态轨迹，而这条轨迹是由个体不同年龄状态组成的，而这些状态可以是联合状态形式，也可以是单状态形式。

表1 状态轨迹序列示例表

四、序列分析方法的实现步骤和功能

Abbott认为序列分析方法是状态轨迹分析的有效工具[13]。而近年来，国外不少学者开始广泛应用序列分析方法，基本思路是首先根据所采集的受访者信息构建其状态序列，而后通过最优匹配方法计算不同个体状态序列的距离矩阵(序列间的差异)，同时可以用相关指数来测量状态序列的内在复杂性，然后再以距离矩阵为基础利用聚类分析方法形成状态序列的不同类型，并以聚类后得到的状态序列轨迹类型为因变量进行统计模型分析。一般而言，序列分析主要包括以下三个步骤：一是理论上设定状态空间和转换成本；二是用最优匹配方法计算成对状态序列的距离矩阵；三是进行多维度测量或者聚类分析，运用聚类分析结果作进一步的模型分析。具体而言，序列分析可以实现以下统计功能或目的：

其一，描述状态序列的年龄分布与状态轨迹序列的变化形态。序列分析具有描述性分析的功能，不仅可以描述不同年龄特定状态的分布，而且可以描绘个体的纵向轨迹形态，即可以通过状态分布图(State Distribution Plot)和序列指数图(Sequence Index Plot)来分别可视化特定状态的年龄分布和轨迹形态。此外，序列分析还可计算众数状态、状态平均持续时间、出现频次最多的状态序列、状态转换次数以及代表性状态序列等统计指标，从而可以深入探索状态序列的特征和内在结构。

其二，综合测度状态序列轨迹。通过计算度量个体特定状态序列轨迹复杂性的熵指数，可以实现状态序列轨迹变化的综合测量。熵是一个来自于信息理论的概念[14]，主要测量状态分布的不确定性和多样性。熵分析被应用到序列分析方法中，用于考察个体状态序列的异质性[15]。熵指数包括横向熵指数(Transversal Entropy Index或Cross-sectional Entropy)和纵向熵指数(Longitudinal Entropy)。熵指数开始被用来描述不同年龄或时点的状态多样性，即计算不同时点或不同年龄上个体特定状态的熵指数，以比较不同时点或年龄上个体间特定状态分布的异质性，称之为横向熵指数。同时，熵的概念也可以应用于定义个体纵向的连续状态序列，称为纵向熵指数，此时熵提供的是状态序列内多样性的度量[16]，即纵向熵指数是以每个个体为基准，通过计算每个个体的熵指数以测量不同个体内状态序列的复杂性。

横向熵指数用于测量状态的多样性以及状态分布的不确定水平，即计算不同时间点上不同个体状态的差异性，如同一年龄不同个体状态的分布差异。假定有两个状态，当一个状态出现的可能性与另一个状态相同，随机选择个体状态的不确定性最大。当一个状态出现的可能性比其他状态高，则不确定减少。如果每个人都具有相同的状态，则没有不确定性，其计算公式如下所示，其中式(2)为标准化的横向熵指数。其中，Pi代表状态的横向比例分布。当所有的个体都具有同样的状态时，H为0；当状态是等频率出现时，H达到最大。

(1)

(2)

纵向熵指数计算个体内状态序列轨迹的复杂变化，纵向熵指数通常采用标准化的形式，以便于比较。式(3)为标准化的纵向熵指数计算公式，其中Pi代表状态i在不同时间点的状态序列中所占的比例。基于不同状态的时间消耗(Time Spent)，纵向熵指数根据每个序列来计算个体的熵指数，进而量化序列状态的复杂性。当一个个体的状态序列在观察期内保持相同的状态，则其纵向熵指数为0；当序列中的每个状态具有相同的数量，则其纵向熵指数达到最大。

(3)

其三，识别状态序列轨迹的不同类型。序列分析中，主要是通过最优匹配方法计算特定状态序列的成对距离矩阵，并以此作为聚类分析的基础，挖掘状态序列的内在模式。最优匹配方法的基本思想是通过考虑将一个状态序列转换为另一个状态序列所需要的努力(Effort)或成本(Cost)以测量两个状态序列的距离或不相似性(Dissimilarity)，从而得到不同个体特定状态序列之间的距离矩阵。转换序列通常需要三种基本操作：一是插入(Insert)，将状态插入到序列中；二是删除(Delete)，从序列中删除一个状态；三是替代(Substitute)，一个状态被另一个状态替代。但是通常会将第一步的插入与第二步的删除进行合并处理，称之为Indel(即Insert+Delete)。对于每个基本操作，可以设定特定的成本，即一个状态序列转换为另一个状态序列所要付出的信息损失代价，而两个状态序列之间的距离被定义为将一个状态序列转换成另一个状态序列的最小成本。然而，成本的设定具有一定的主观性，通常是根据理论或数据特征进行设定，或是直接设定为固定值。

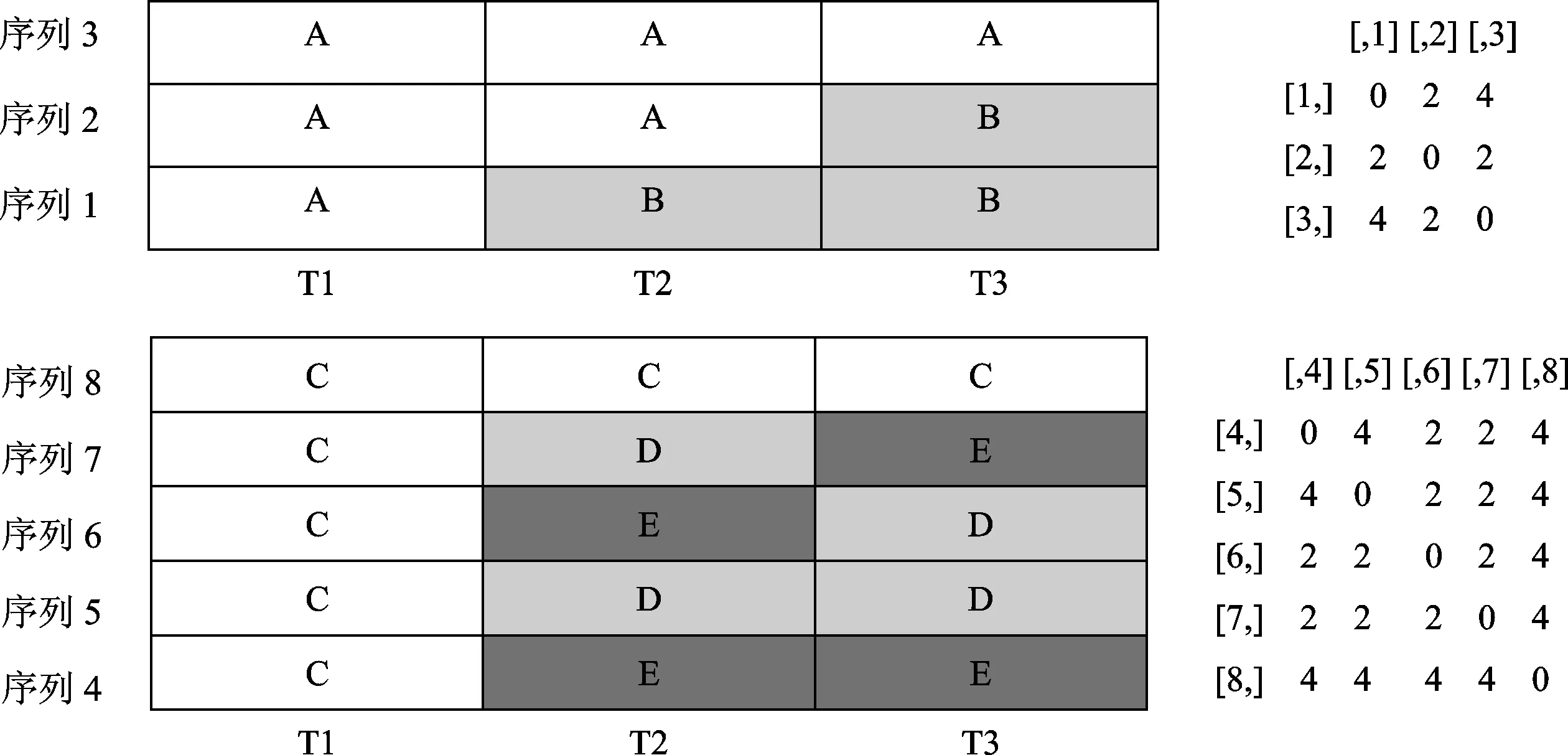
图1 最优匹配计算距离示例图

注：A、B、C、D、E分别代表不同的状态，T1、T2、T3分别代表三个不同的时间点或年龄，图中每一行代表一个序列，图右侧的矩阵为不同个体状态序列的距离矩阵。

如图1所示，第一个状态序列与第二个状态序列有一处不同，故其距离为2；而第一个状态序列与第三个状态序列有两处状态不同，因此其距离为4。而对于状态序列4到8来说，是更为复杂的状态序列轨迹，所以其计算距离也就需要更多的步骤，状态序列4与状态序列6的距离为2，因为两个序列有一个时点的状态存在差异，而状态序列5与状态序列8的距离为4，因为两个状态序列存在两个时点上的状态差异，状态序列6与状态序列7尽管有两个时点上的状态存在差异，但仅通过一步就可以将两个状态序列进行匹配，所以其距离为2，其他状态序列的距离计算也相类似。在设定了插入与删除以及替代的成本、计算状态序列的距离后，需要根据距离矩阵对状态序列进行聚类分析，以探索个体状态序列的类型，即利用Ward等算法进行层次聚类分析以实现数据的降维处理，从而将序列组织成组，使得组内序列的相似度最大化。聚类的有效性可以通过一系列的指标来检验，借助这些指标标准能够找到最佳聚类数目，实现聚类水平的稳定和个案信息的最大占用。此外，可以根据具体的研究问题和设计，以聚类分析得到的状态序列类型为结果变量，通过拟合Multi-nomial logistic回归模型来分析不同特征变量对状态序列类型归属概率的影响。

五、应用举例

本文以就业状态的变化轨迹为案例，进一步阐释序列分析方法的应用价值。案例所使用的数据来自于中国健康与养老追踪调查(China Health and Retirement Longitudinal Study，CHARLS)2014年开展的第三次追踪调查，即“中国老年人生命历程调查”数据，此次调查以中国45岁以上的中老年人家庭和个人为调查对象，通过回顾性的方式采集了老年人的教育史、生育史、婚姻史、就业史等主要领域的信息。本案例主要根据受访者的教育史和就业史信息形成个体教育到就业的状态序列，然后利用序列分析方法描述个体的就业状态序列的年龄分布和轨迹形态，测量就业状态序列的复杂性以及形成就业状态轨迹的类型，状态序列的统计分析均在R软件中实现。

(一)就业状态空间的确定

对于从教育到工作的状态轨迹而言，由于教育与就业的发生具有先后次序性，所以将两者合并为一个领域，把教育也看作工作的一种特定状态，即从教育到工作的状态序列属于单维的状态轨迹，故选择教育与就业领域的在学、农业在业、非农在业、参军服役、不在业5个状态，上述5个状态的表示方法分别为：ED代表在学、AG代表农业就业、NA代表非农就业、MS代表参军服役、而UN代表未在业，进而构成了个体在不同年龄的教育或就业状态序列。

(二)描述状态序列的年龄分布与状态序列的轨迹变化形态

所谓状态序列的横向描述性分析主要是对不同年龄(段)的状态进行描绘，以呈现不同年龄的状态分布以及随年龄变化的模式，从而探索状态的分布和变化特征。基于状态序列的时间单位，可以描绘不同时间单位上的状态分布情况，如在某一月份或年龄上的状态分布。由于本案例的时间单位是年，因此图2所描述的是个体在不同年龄(10～45岁)所处的教育或就业状态分布，每一种颜色代表着不同的状态，这类统计图形即为状态分布图。

图2 就业状态序列的横向分布描述图

由图2，整体而言，就业状态的年龄分布具有一定的主导性状态，并且呈现梯次变化。所谓个体状态序列的纵向描述，是指用序列指数图对个体的状态序列轨迹进行整体描绘，序列分析将每一个人的就业状态轨迹看作一个单独的状态序列，从而可视化个体在特定时间内的就业轨迹。在本案例中，即是用序列指数图对个体从10岁到45岁的就业状态轨迹进行刻画，该类图形中的每一栏代表一个个体的状态序列轨迹。限于篇幅，序列指数图并未在此呈现。

(三)综合测度状态序列轨迹

序列分析融合了熵指数测量状态的多样性和复杂性，综合性测度的结果代表个体状态序列的稳定性水平。图3呈现了横向熵指数的结果，横向熵指数用来测量个体在不同年龄上状态的多样性，即分年龄的状态多样性。由于横向熵指数值是根据不同个体在相同年龄时的状态来计算的，因此，对于横向熵指数而言，值越大代表某一年龄的状态越多元，而值越小则意味着某一年龄的状态较为平稳。根据图3所勾画的横向熵指数总体分布，其大致经历了先增大后减小的总体趋势，呈现倒“U”型形态，说明人们就业状态的多样性经历了先上升后平稳的过程，在20岁时就业状态的多样性最为突显。纵向熵指数值越大代表着个体就业状态序列的差异或不相似性越大，而纵向熵指数值越小代表着个体就业状态序列的差异越小，即个体就业状态更为平稳简单。总体而言，个体就业状态的纵向熵指数的数值范围在0～1之间，其最小值为0，最大值为0.976，平均值为0.371，第一个四分位数为0.251，中位数为0.349，第三个四分位数为0.503，纵向熵指数数值的分布集中性，表明个体就业状态序列的一致性程度相对较高。

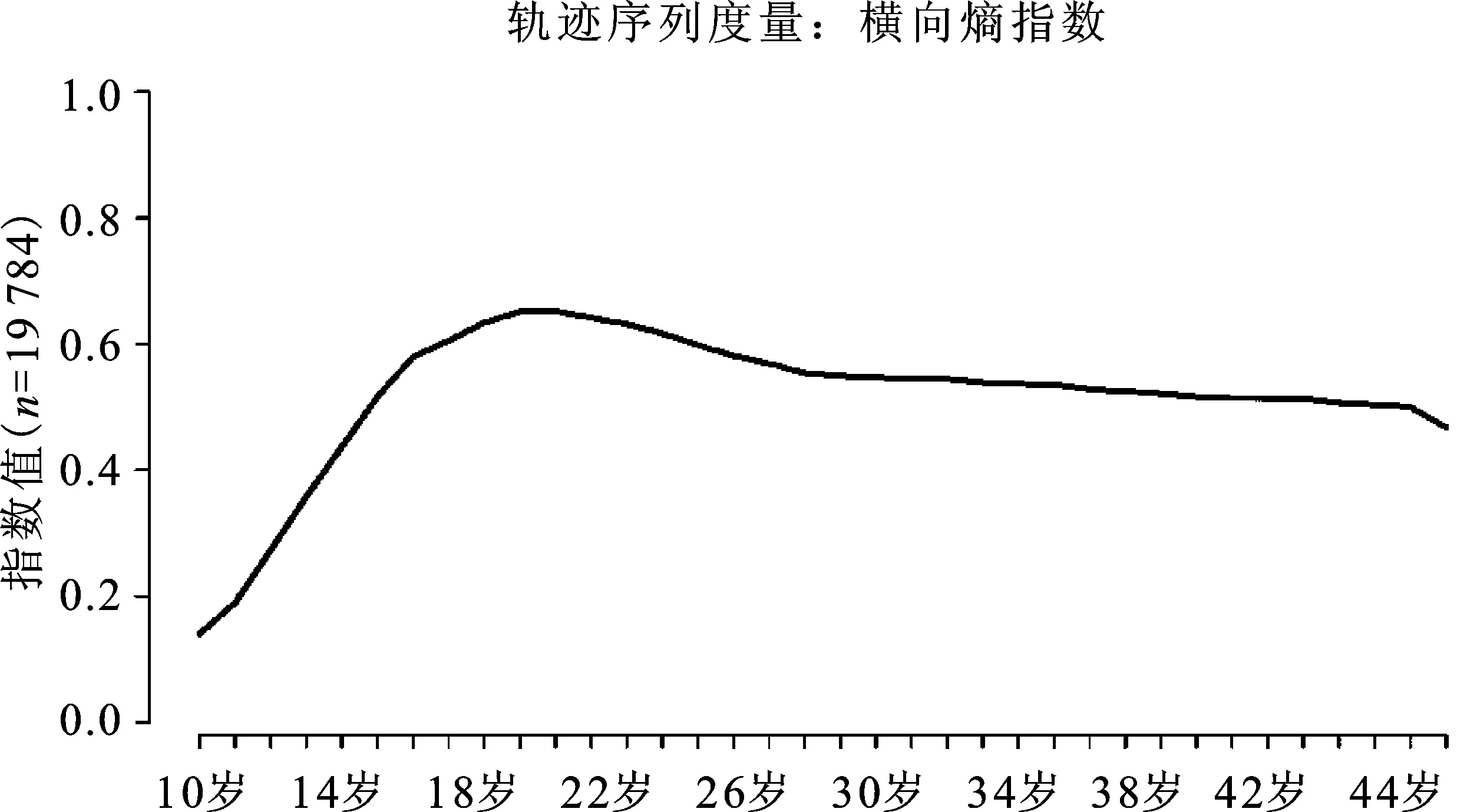
图3 就业状态测试之横向熵指数结果图

(四)识别状态序列轨迹的不同类型

如上所述，为了识别状态序列轨迹的模式类型，序列分析结合了最优匹配和聚类分析技术，即通过最优匹配方法计算特定状态序列的成对距离矩阵，并以此距离矩阵为基础，运用聚类分析技术挖掘状态序列的内在结构类型。在最优匹配的转换成本设定上，本案例将状态之间的转换率作为替换的成本，而将插入与删除的成本设定为固定值1。下图呈现的即为聚类分析所识别的就业状态序列的不同类型。

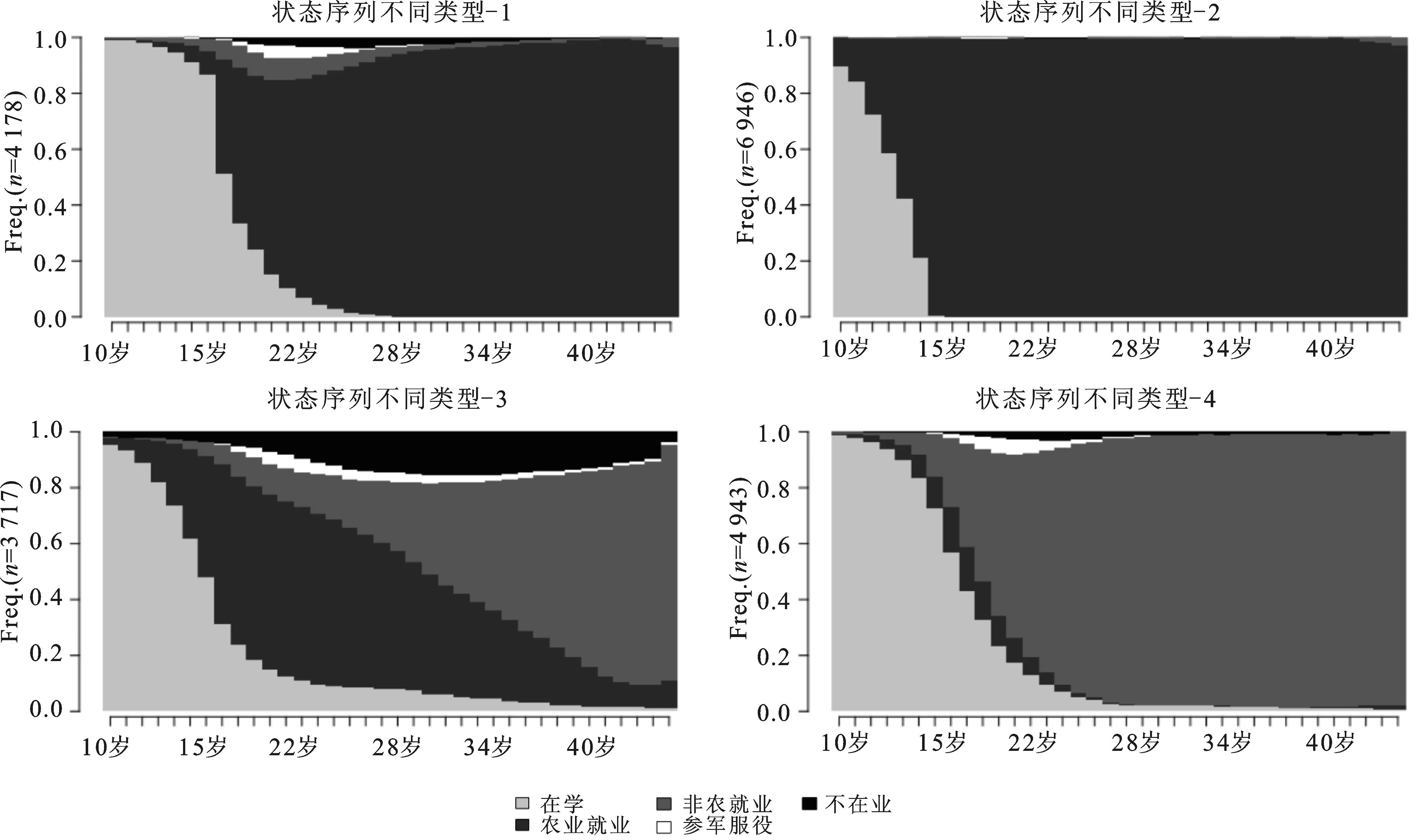
图4 就业状态序列的不同类型图

根据图4，第一个类型的特征是成员教育水平较高但从事农业就业，第二个类型的特征为个体的受教育程度水平低且从事农业就业，第三个类型的成员经历了从接受教育到农业就业再到非农就业的状态递度转变，而第四个类型则主要由教育水平高和非农就业的个体组成。表2给出了聚类分析结果的检验标准，综合表中各指标来看，聚类分析能够识别轨迹序列的内部结构，聚类分析的效果有效地呈现了不同聚类类别的差异，使类别内部相似性最高，而类别之间的差异性最大。

表2 聚类分析相关检验指标表

六、总结和展望

近十几年来，随着研究者对状态变化时序性的关注，用于分析状态变化形态的序列分析方法得到发展和应用。序列分析方法是用于识别和挖掘随时间或年龄变化的状态序列轨迹的统计分析工具，其基本思路是：首先利用相关数据资料构建状态序列，利用系列指标对状态序列进行描述性分析，而后通过最优匹配方法计算不同个体状态序列的距离矩阵，同时还可以用熵指数测量状态转换的频度以捕捉状态序列的内在复杂性，然后再以计算得到的距离矩阵为基础运用聚类分析方法形成状态序列的类型，而通过聚类分析得到的状态序列类型可以作为进一步多元统计分析的基础。应用序列分析方法主要包括三个步骤：理论上设定状态空间和转换成本、用最优匹配算法生成成对状态序列的距离矩阵以及进行多维度测量或者聚类分析，并运用聚类分析结果作多元统计分析。序列分析方法具有三项主要功能：描述状态序列的年龄分布与状态轨迹序列的变化形态、综合测度状态序列轨迹、识别状态序列轨迹的不同类型以及事后统计分析。

序列分析方法为开展状态序列有关的研究提供了有效的分析手段。序列分析作为一种统计分析方法，其衍生发展不仅是统计学研究领域的突破，而且对于不同的学科范式具有工具性价值。在社会科学领域，由于特别关注事实(事件)随时间变化的轨迹，故序列分析方法恰好提供了轨迹挖掘的统计功能[17]。比如，在生命历程研究中，可以分析和可视化个体生命历程状态随年龄变化的轨迹形态，并形成生命历程状态轨迹的模式类型；又如，在人口学中，可以研究从教育到就业的转变轨迹、婚育状态的变迁形态、迁移状态的变化轨迹以及向成年、中年的过渡轨迹等；再如，在犯罪学研究中，可以刻画犯罪行为的状态轨迹，分析犯罪轨迹的动态变化。尽管国内尚未出现运用序列分析方法开展的具体研究，但是相信随着该方法不断被研究者所熟知，序列方法的应用和适用范围会不断拓展。特别是当前中国正经历着急剧的社会变迁过程，社会结构不断变化、社会流动性增强，个体的生命、生活、工作状态多样性增长，而序列分析恰为研究者描述社会的时变、群体或个体生命、生活状态的流变提供了适宜的分析方法，成为透视中国社会发展变迁的有效研究工具。