又一“点关于直线对称”的公式
2019-04-12四川省绵阳第一中学621000郑中荣
四川省绵阳第一中学(621000) 郑中荣
高中课堂教学离不开解题教学.在解析几何中,涉及到点关于直线对称的习题很多,然许多同学在解相关题型时感觉计算繁琐,且容易出错.为了解决此困难,笔者对点关于直线的对称问题进行了探索,给出了一个非常简洁的计算公式,相信能对广大读者有所帮助.
问题求点N(x0,y0)关于直线l∶Ax+By+C=0 的对称点M的坐标.
设M点的坐标(x1,y1),由一般做法:
文[1]给出了一个改进公式:
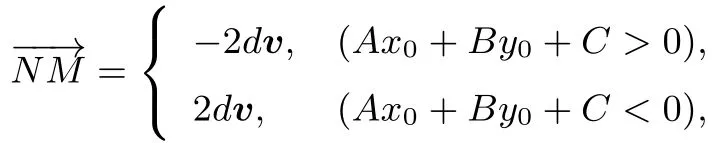
(v=d表示N到直线的距离.记作(公式二).
文[1]对(公式二)给出了一种证明,但笔者在研究时发现利用圆的知识证明更直观易懂.证明如下:
证明(如图1),M,N是圆C直径上的两个端点,且关于直线l∶Ax+By+C=0 对称.v是与l垂直的单位向量即N到l的距离为d=R,则=-2Rv=-2dv(Ax0+By0+C>0)或=2Rv=2dv(Ax0+By0+C<0).从而得到(公式二).

图1
图2
公式(二)的形式较公式(一)简化了许多,为计算带来了一定简便.但在解题时,计算步骤还是较多,不光要计算点到直线距离和与l垂直的单位向量,还需判断Ax0+By0+C>0(<0).为此笔者对这个公式继续探索,在研究的过程中,发现它与圆的知识联系非常紧密.M,N两点不仅可以看作圆C直径上的两个端点,甚至还可以看作关于直线l对称的两个圆的圆心(如图2),再利用圆的相关知识推导出点关于直线对称的另一非常好用的公式:其中:记为(公式三).
证明不难发现,我们熟知的圆系方程x2+y2+Dx+Ey+F+λ(Ax+By+C)=0 ((D+λA)2+(E+λB)2-4(F+λC)>0)其图形表示圆心在过且 与l∶Ax+By+C=0垂直的直线上的圆.故不妨设以N(x0,y0)为圆心的圆的方程:x2+y2-2x0x-2x0y+K=0(x20+y20-K>0),则圆M的方程可设为:x2+y2-2x0x-2y0y+K+λ(Ax+By+C)=0((2x0-λA)2+(2y0-λB)2-4(K+λC)>0),从而得出M的坐标又因为MN的中点在直线l∶Ax+By+C=0 上,所以解得这样得出M的坐标计算公式:其中:
显然,公式(三)较上面两个公式形式更简洁,并且容易记忆,不需要判断Ax0+By0+C的符号,计算非常方便.我们如果再将公式(三)改变一下,得到这样的形式:
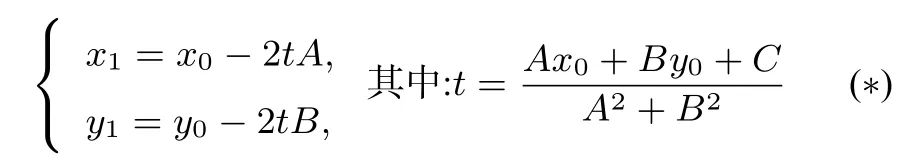
亲爱的读者朋友们,在这里你们是否发现t=与点到直线的距离公式很相似,是否觉得该公式很具几何意义呢,你们是否发现它就是直线的参数方程形式呢? 这是否也体现了数学的和谐性呢? (∗)式让我们在计算点关于直线对称问题上告别了复杂、繁冗的计算过程,让数学运算变得简单.
下面我们用几道具体例子来体验一下极速的感觉:
例题一束光线m从P(6,4)出发,经过l∶4x+3y=11反射后,通过点Q(-4,3),求反射光线的方程.[人教A 版必修2P101 改编]
解设M(x1,y1)是P关于l的对称点,由(∗)式得t=1,x1=-2,y1=-2,故M(-2,-2).又点M在反射光线上,从而得出反射光线得方程:5x+2y+14=0.
练习
1.求与圆C∶(x+2)2+(y-6)2=1 关于直线3x-4y+5=0 对称的圆的方程.[人教A 版必修2P144]
2.△ABC的顶点A的坐标(5,1),∠B,∠C平分线的方程分别为x-2y=0 和x+y-1=0,求BC所在直线方程.[人教A 版必修2P110 改编]
答案1.由(∗)式得t=-1,C关于直线的对称点C1(x1,y1),则x1=4,y1=-2,故所求圆的方程:(x-4)2+(y+2)2=1.
2.由(∗)式得点A关于直线x-2y=0 和x+y-1=0的对称点分别是又对称点均在直线BC上,所以得出直线BC的方程
结束语:著名数学家乔治·波利亚指出:“中学数学的首要任务就是加强解题训练”.怎样引导学生避免题海战术,在数学知识海洋上探索是我们的重要任务.笔者在研究新课标时,注意到:“运用代数方法进一步认识圆锥曲线的性质以及它们的位置关系,运用平面解析几何方法解决简单的数学问题和实际问题,感悟平面解析几何中蕴含的数学思想.”[2]“能用直线和圆的方程解决一些简单的数学问题与实际问题.”[2]故本文这一公式显得非常重要.
通过本文对公式的推导,让我们认识到同一数学知识可以有多种不同的存在形式,而同一数学形式又可以从多个数学知识上去理解和认识.在解题的过程中,学生缺少的是对解决问题的探索.因此我们教师在教学中,要注重引导学生探索解题规律和技巧,让数学的教与学变得更加有趣.
