基于改进型CNN的多聚焦图像融合方法
2019-04-12孔韦韦赵文阳
孔韦韦,雷 阳,任 聪,赵文阳
(1.西安邮电大学 计算机学院 陕西 西安 710121;2.武警工程大学 密码工程学院 陕西 西安 710086)
0 引言
目前,主流的多聚焦图像融合方法可分为变换域融合方法与空间域融合方法两类.代表性变换域融合方法主要基于多尺度几何分析理论展开,可分为源图像多尺度分解、子图像融合以及最终图像重构3个步骤.经典的小波变换仅能捕获有限方向的图像特征,且不具备平移不变性,非下采样轮廓波变换[1-2]与非下采样剪切波变换[3-7]作为经典轮廓波变换与剪切波变换的改进型模型,极大地提升了图像的融合效果.然而,在此过程中,信息的损失和光谱信息的扭曲仍然是无法回避的问题.与多尺度几何分析方法不同,稀疏表达[8-10]模型侧重于将源图像转换为单一尺度的特征映射,并采用滑动窗口实现平移不变性图像融合的近似表达,该模型具有较好的图像融合效果,但在源图像高频细节信息保存方面略显不足.相比变换域融合方法,早期经典的空间域融合方法通常采取将源图像划分为若干块,而后选取空间频率或梯度信息等评价指标分别对源图像的对应块加以比较和融合.但是图像块的尺寸以及融合规则的选取通常会对最终融合效果造成很大的影响.因此,目前主流的空间域方法主要着眼于图像块尺寸的自适应调整以及融合规则的设定.
CNN作为深度学习中的代表性模型,由于具有优越的图像特征捕捉和信息分析能力,被广泛应用于图像识别、图像检索等领域.本文采用CNN模型对多聚焦图像融合问题加以解决.针对多聚焦图像融合问题与CNN中分类问题的一致性,探索二者的切合点以及本文方案的可行性;对经典的CNN模型加以优化,构建改进型CNN模型;将待融合源图像输入到改进型CNN模型进行实验仿真.仿真结果表明,与现有的代表性融合方法相比,该方法无论在直观视觉效果还是客观评价指标值均具有显著的优势.
1 一致性关系研究
CNN是一个可训练的多层前馈人工神经网络,且每一层都包含与抽象层相对应的一定数量的特征映射.其中,特征映射中的每个单元或系数称为神经元.线性卷积、非线性激活和空间域池化用于实现不同阶段特征映射的连接.图1给出了经典CNN模型结构图.
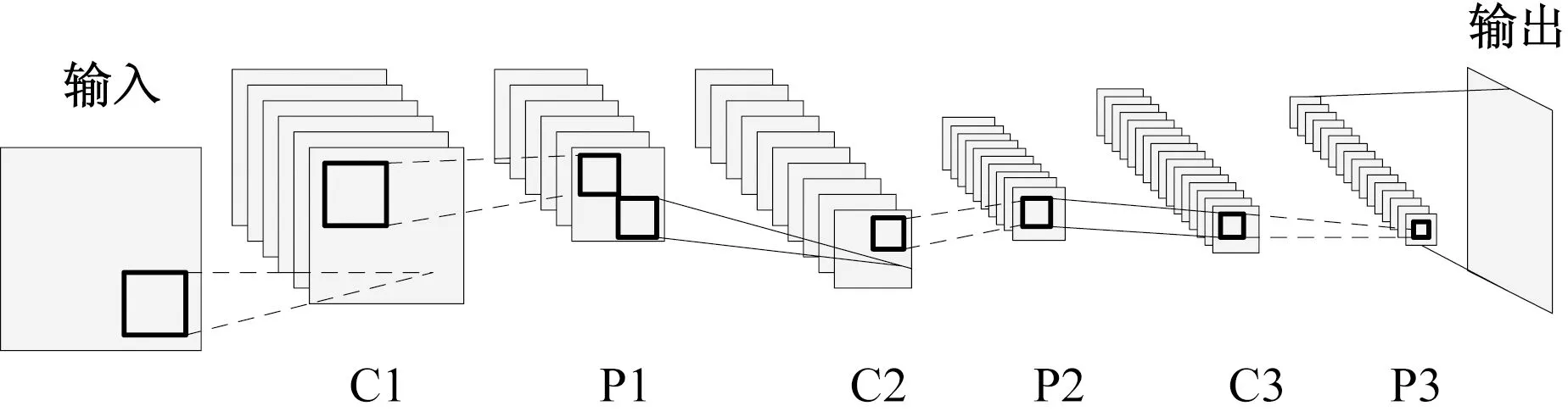
图1 经典CNN模型结构图Fig.1 Structure of the traditional CNN model
图1中的CNN模型拥有1个输入层、1个输出层、3个卷积层以及3个池化层.输入层/输出层用于接收/输出图像信息;CNN的第一卷积层的滤波器主要用于检测低阶特征,比如边、角、曲线等.随着卷积层的增加,对应滤波器检测的特征也更复杂.例如,第二卷积层的输入实际上是第一层的输出,该层滤波器用来检测低阶特征的组合等情况(半圆、四边形等),如此累积,以检测越来越复杂的特征.池化层周期性地出现在相邻的两个卷积层之间,可以有效减少训练参数的数量,压缩图像的空间大小.
CNN模型中滤波器激活图源于特征提取,而融合规则的作用恰恰类似于分类任务中使用的分类器.就现行绝大多数空间域和变换域方法而言,激活映射图可以通过构造局部滤波器来获取源图像的高频细节信息,而融合规则实质上完成了针对源图像像素点的权值分配.CNN模型中的“卷积”操作与多聚焦图像融合过程中的滤波器操作等价,而多聚焦图像的焦点映射图生成过程等价于CNN模型的分类过程.因此,可以采用CNN模型用于图像融合问题的解决.
2 改进型CNN模型
针对经典CNN模型中权值设置随意,以及部分结构不合理的问题,提出并构建一种改进型CNN模型,该模型主要涉及权值设定、卷积层和池化层3个部分.
2.1 权值设定
经典CNN模型涉及大量权值的设定,这些权值设置通常较为随意,而权值设定的优劣直接影响CNN模型的训练效果以及最终的分类结果.针对该问题,本文提出采用高斯概率分布函数确定输入层与第一卷积层(C1)、池化层与相邻后续卷积层间的权值,
其中:矩阵P中每一元素的尺寸均为r×r;N表示卷积核的数量.显然,若前一层图像信息的尺寸为k×k,则通过高斯概率分布函数获得的特征映射图的尺寸为(k-r+1)×(k-r+1).
2.2 卷积层
卷积层主要针对源图像或前一池化层中的特征映射采取“卷积”操作,以提取图像中的特征信息.有了2.1节的权值设定,可以得到第i幅特征映射中位于点(x,y)的卷积结果为
其中:Θ表示待融合源图像.需要说明的是,不同于经典CNN模型,特征映射并不适用于非线性函数.
2.3 池化层
池化层通常周期性地出现在相邻的两个卷积层之间,其功能主要在于有效减少训练参数的数量,从而压缩图像的空间大小.经典CNN模型采用平均值池化层策略和最大值池化层策略.然而,这两种策略均有不同程度的缺陷.其中,平均值池化针对每个池化邻域内的结点进行算术平均运算,但会削弱强激活结点产生弱池化效应;最大值池化倾向于过度拟合训练集从而影响泛化性能.为了克服这两种经典池化策略的消极影响,本文提出了均方根池化策略.
大量仿真实验结果表明,即使随机设定若干权值,均方根池化策略仍然具有固有的频率选择性和平移不变性.该池化策略具有平方运算和求和运算两个部分,可以使整个CNN模型具有很好的非线性和平移不变性.将均方根池化策略应用于所有池化层,可以得到点(x,y)位于第j幅池化映射中的结果为
其中:Θ表示待融合源图像;p,q=1,…,(k-r+1);e为池化邻域半径.
3 实验仿真
为了验证文中提出的融合方法的有效性,本节将引入几种近年代表性的方法与之进行比较.本文的实验平台为一台CPU,主频为2.9 GHz、8G内存的PC,采用的仿真软件为Matlab 2014b.本节选取了两组灰度图像作为源图像进行融合仿真实验.
3.1 融合方法及量化评价指标
本文将采用性能较为优越的4种融合方法与文中方法(记为M5)进行融合效果比较:基于框架变换耦合SUSAN的多聚焦图像融合算法[11](M1)、基于小波变换的多聚焦图像融合方法[12](M2)、基于NSCT耦合区域特性的多聚焦图像融合算法[13](M3)、基于多尺度CNN和图像分割的多聚焦图像融合算法[14](M4).其中M1~M4中的参数均按照原对应文献中的给定数据设定.本文所提方法的改进型CNN模型具有1个输入层、1个输出层、3个卷积层(3个卷积层的滤波器数量分别为5、10、15,且所有卷积核的尺寸均为3×3),3个池化层(池化层最后一层的邻域尺寸设定为2×2,其余池化层的邻域尺寸设定为5×5).
除了直观视觉效果外,本文还采用了4种客观评价指标比较5种方法的性能,分别为空间频率(spatial frequency,QSF)、Piella指标(QPiella)、互信息量(mutual information,QMI)和相位一致性(phase congruency,QP).QSF是衡量图像像素点信息反差度的重要指标,融合图像的QSF值越大,表明融合图像的信息量越丰富,融合质量越好;QPiella描述了图像的结构信息,QPiella值越大,图像的结构信息越丰富,效果越好;QMI用来衡量融合图像与源图像间的交互信息,QMI值越大,表示融合图像从源图像中获取的信息越丰富,融合效果越好,本文使用的是归一化互信息量;QP利用相位一致性描述图像边缘信息,QP值越大,表明融合图像的边缘信息越丰富.以上各指标的表达式参见文献[15].
3.2 多聚焦图像融合实验
本节选取两组灰度图像作为待融合源图像,图像像素大小均为512×512.该两组图像分别拥有不同的聚焦信息,如何尽可能地将这些聚焦信息融合到一幅结果图像中是本节实验的主要目的.M1~M5 5种方法的图像融合仿真效果如图2~3所示.

图2 第I组多聚焦图像融合效果图Fig.2 Fused results of the multi-focus images in group I

图3 第II组多聚焦图像融合效果图Fig.3 Fused results of the multi-focus images in group II
从直观角度看,上述5种方法均较好地保持了两幅源图像的重要信息,并对源多聚焦图像进行了较好的融合.为了更方便进行比较,本节针对融合结果图像中的部分显著区域进行了放大,如图4所示.本文方法的融合结果图具有更理想的视觉效果.此外,直观效果在客观评价指标数据中也得到了验证,表1和表2给出了5种融合算法的客观评价测度值.

图4 五种融合方法的区域放大图Fig.4 Enlarged images based on five methods

表1 第I组灰度多聚焦图像融合效果性能比较Tab.1 Performance comparison of the grey multi-focus images in group I
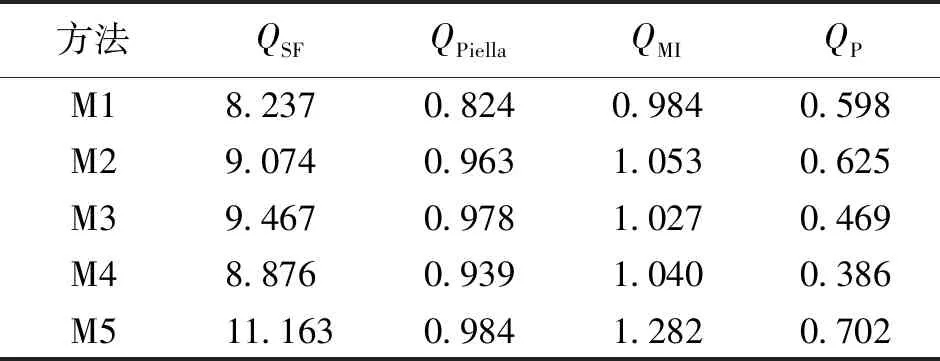
表2 第II组灰度多聚焦图像融合效果性能比较Tab.2 Performance comparison of the grey multi-focus images in group II
如上所述,与现有代表性融合方法相比,本文提出的融合方法无论在直观视觉效果还是客观评价指标值方面均具有较明显的优势.
4 结论
本文针对多聚焦图像融合问题,提出了一种基于改进型CNN模型的图像融合方法.论述了多聚焦图像融合问题与CNN中分类问题的一致性关系,表明了本文方法的合理性和可行性;对经典的CNN模型加以改进,给出了权值设定方法,并对经典模型的池化层机制进行了改进;将待融合源图像输入改进型CNN模型进行了实验仿真.仿真结果验证了本文方法的有效性.
