一种聚集性面群中毗邻区自动识别与处理方法
2019-04-11李成名武鹏达刘晓丽
李成名,殷 勇,武鹏达,刘晓丽
1. 中国测绘科学研究院,北京 100830; 2. 空天地海一体化大数据应用技术国家工程实验室, 陕西 西安 710072
毗邻化(agglomeration)是保持具有毗邻特性的聚集性面状要素群(简称毗邻区)结构化特征的几何变换,具体地讲,是指通过将毗邻区内的狭长空白分割(简称桥接面)收缩为线,从而使被其分割的相离面要素成为毗邻面要素的几何变换过程[1]。当地图表达的比例尺从大变小时,图上毗邻区内部的带状桥接面由于较为狭长难以在图上表现,而现实应用中又要求其结构特征必须保持,故毗邻化操作十分重要。
文献[1]率先提出了毗邻化操作的基本原理,即以空间叠加分析获取桥接面,并基于Delaunay三角网提取桥接面骨架线的方式实现聚集面群的毗邻化;文献[2—3]进一步总结并细化了毗邻化实现的具体思路;文献[4—5]将毗邻化操作应用于水系要素中的散列湖泊、养殖水域多边形等要素的综合,并形象地将沿着骨架线将多边形边界进行缝合的毗邻化过程形容为“拉上拉链”,通过试验验证了良好的处理效果。然而,这些研究建立在一个假定前提下,即适合进行毗邻化操作的聚集性面状要素群(即毗邻区)已确认。在实际的地图数据中,面要素通常离散分布在各处,这一假定通常不成立,故如何准确识别毗邻区是一个难点和重点;另外,对于边界存在凹凸结构的复杂毗邻区,如何合理、准确地完成其毗邻化也是一个难点。针对以上两点,本文提出了一种聚集性面群中毗邻区自动识别方法,并对现有的毗邻化操作方法进行了改进,增强普适性。
1 相关工作
1.1 现有毗邻化方法
文献[2]给出了毗邻化操作的实现思路:计算聚集面群的最小外接矩形(minimum bounding rectangle,MBR),并通过最小外接矩形对原始面群求补,从而提取面群之间狭长桥接面,并将其转换为可操作的面要素,进而计算其骨架线,作为面群新的边界线,达到毗邻化操作的目的,如图1所示。
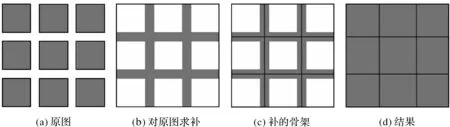
图1 矢量多边形的毗邻化Fig.1 Agglomeration of vector polygon
1.2 现有毗邻化方法存在的不足
毗邻化操作是由计算最小外接矩形、提取桥接面等几个关键算法组合而成的地图综合操作,但它并不是上述几个算法的简单叠加,而是要求综合前后具有毗邻特性的聚集性面状要素群(毗邻区)具有一致的几何边界轮廓,桥接面骨架线具有与桥接面一致的主体形状及延展性,并能准确反映要素之间的邻近关系。由于实际地图数据的复杂性,现有方法存在以下不足:
(1) 形状多样的面要素通常无规律地分布在一定的地理区域内,根据其形状及结构特征识别出具有毗邻特性的聚集面群(毗邻区)是实现毗邻化自动处理的重要前提,但现有研究均未对此给予足够的关注。
(2) 实际地物边界轮廓并不规整,通常带有凹凸结构。当使用凸壳、最小外接矩形(MBR)或最小面积外接矩形(minimum area bounding rectangle,MABR)[6-7]对其外边界进行概括时,存在冗余的边界空间,如图2所示,现有方法在毗邻化过程中对原图求补时,所得结果比真实面积大,如图2(c)中阴影部分所示,这些冗余空间会导致骨架线的误提取。
(3) Delaunay三角网因具备邻近性、最优性、区域性、凸多边形等多种优异特性[8-9],常被用于面要素骨架线提取,但据此提取的主骨架线并非是毗邻化操作的最优骨架线(称为毗邻化线)。由桥接面获取方式可知,毗邻区中各个面要素自身的几何凹凸结构同样会反映在桥接面的几何形状中,并对桥接面边界处的骨架线取舍有直接影响。若依骨架线长度或骨架线所占三角形面积作为最优骨架线的判别选取标准,容易造成骨架线的误提取,如图3所示。依据主骨架线提取方法,则凹陷结构处形成的骨架线OB会取代OA成为最优骨架线,末端节点受凹陷部分影响并非落在边界,这是不合理的。

图2 面群最小面积外接矩形示例Fig.2 MABR of area group
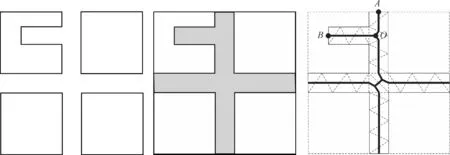
图3 最优骨架线末端点未落在边界Fig.3 The end point of the optimal skeleton line does not fall on the boundary
2 一种毗邻区自动识别及处理方法
本文所提方法的核心包括3部分:①毗邻区自动识别。总结提炼毗邻区的典型结构特征,并基于这些特征渐进式辨识。②优化外围边界轮廓算法。引入缓冲区变换实现对外围边界轮廓的准确计算。③边界约束下的骨架线修正。以桥接面边界作为约束修正主骨架线,规避其末端节点未落边界的缺陷,形成适宜毗邻化线的最优骨架线。
2.1 毗邻区自动识别
人在视觉感知过程中,往往服从于某些图形特定的组成规律,自然而然地会追求事物的结构整体性或守形性[10],Gestalt心理学的图形理论在这方面进行了深入的研究和讨论[11]。毗邻区是具有毗邻特性的聚集性面状要素群,其通常被狭长条带状桥接面分割且呈集中连片分布状态,因此,对于毗邻区识别,适用的Gestalt原则包括:邻近性原则(proximity)、连续性原则(continuation)、紧凑性原则(compactness)。遵从上述原则,提炼总结了毗邻区的结构特征,并开展基于这些特征的自动识别。
2.1.1 毗邻区典型特征
2.1.1.1 带状桥接面宽度
(1) 宽度阈值
聚集性面状要素群个体形状多样,带状桥接面宽度(width index,WI)实质上是相邻面要素之间的间距(TBDistance)。假设从原始尺度1∶Oscale综合缩编至目标尺度1∶Tscale(Tscale>Oscale)时,首要任务是通过分割宽度阈值(BWthreshold)来辨识带状桥接面,以确定聚集性面状要素群是否为毗邻区。依据目标比例尺,根据公式(1)计算出宽度阈值。
TBDistance=BWthreshold×Tscale
(1)
(2) 宽度计算
步骤1:利用最小面积矩形计算聚集性面状要素群边界,如图4所示。
步骤2:加密最小面积矩形边界及面群各要素边界节点[12]。因为这些节点通常被用于描述面状地物重要形态特征,如拐点、相交点等,一般数量较少,为提高后续分割宽度计算精度,需加密两类边界上的节点。具体方法为:设定加密步长d,d的取值通常采用要素边界最短弧段的长度;以d为基元在两个节点之间进行采样得到加密点,如图5所示。
步骤3:采用逐点插入算法建立边界约束的Delaunay三角网,如图6(a)所示。
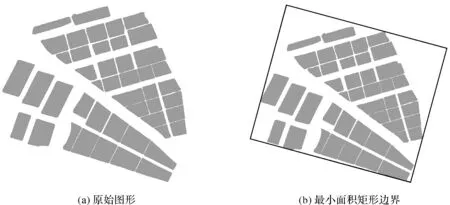
图4 聚集性面状要素群边界Fig.4 Boundary of aggregated area group

图5 面要素节点加密Fig.5 Increasing density for area element nodes
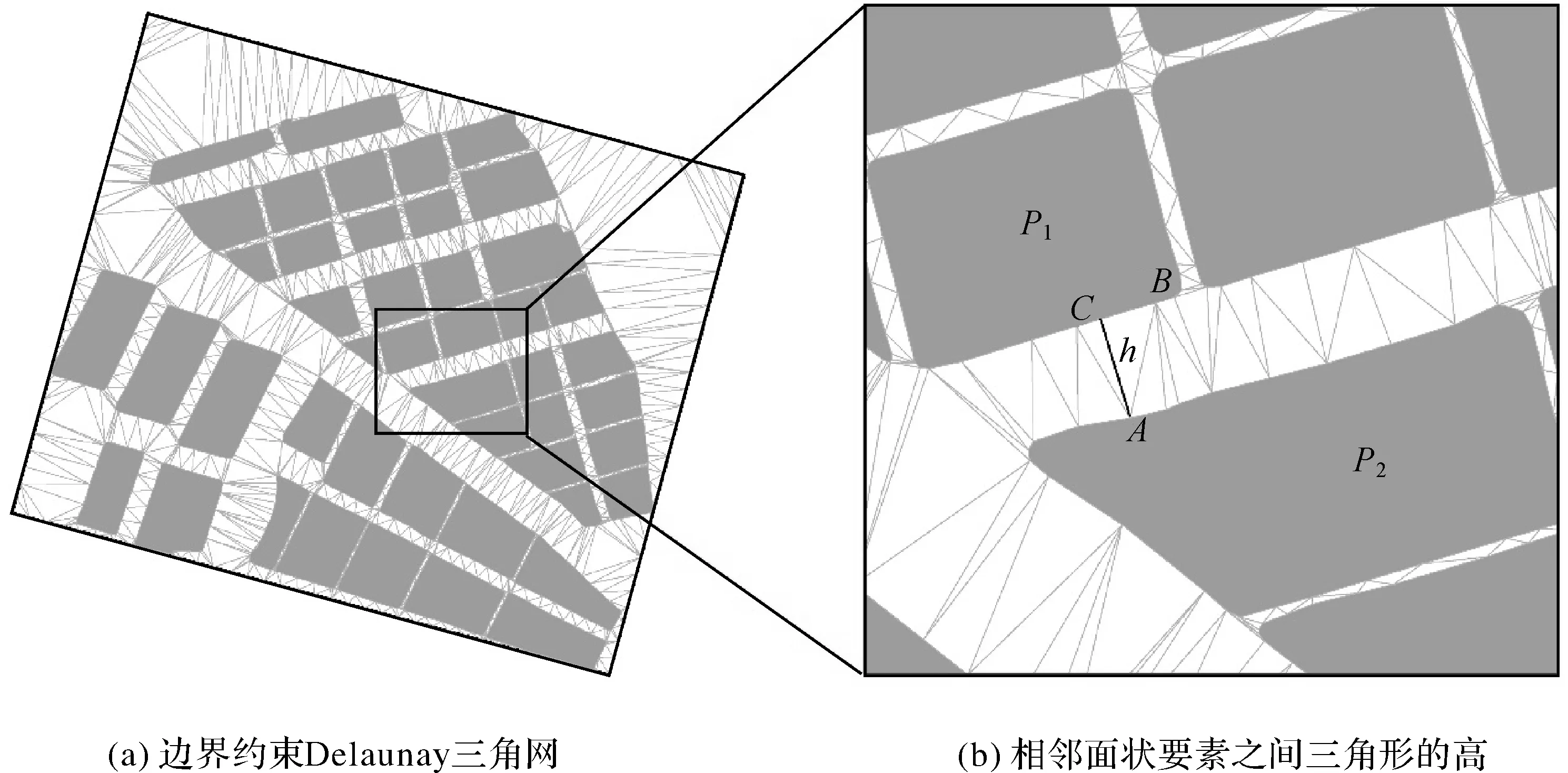
图6 桥接面宽度计算Fig.6 Width calculation of bridging area
步骤4:约束Delaunay三角网中三角形连接了两个具有邻近关系的面状要素,图6(b)为图6(a)中三角网的局部放大。不难发现,通过三角形ABC的边AB或AC很容易获知P1和P2为邻近面状要素。计算两个相邻面状要素之间所有Delaunay三角形的高(在要素边界轮廓上的边所对应的高),并将其平均值作为邻近要素之间的间距(BDistance)
(2)
式中,n为两相邻面之间Delaunay三角形的总个数。
步骤5:根据带状桥接面宽度阈值(TBDistance),若两个邻近面状要素的BDistance≤TBDistance,则识别为候选毗邻区子集,以此类推,提取候选毗邻区全集。
2.1.1.2 有效连接特征
针对彼此邻近的面要素,根据Gestalt连续性原则(continuation),当其中一个面要素某些部分视觉上与另一个面要素连接在一起,那么这两个要素可以认知为一个整体,故判断两邻近要素之间的可连接区域面积在整体中的占比是识别毗邻区的核心指标。本文引入有效连接指数(effective connection index,ECI)来反映该指标。指标计算的具体步骤为:
步骤1:基于边界约束Delaunay三角网,识别连接两邻近要素的Ⅱ类三角形[13-15](有两个邻近三角形的一类三角形),并将其作为两要素之间的连接区域,如图7中黄色及绿色背景区域。
步骤2:计算各个三角形的内角,将内角不包含钝角,且其邻近三角形的内角同样不包含钝角的三角形称为有效三角形。这些有效三角形覆盖的区域称为有效连接区域(connectable area,CA),如图7中绿色背景区域,其他区域称为无效连接区域,如图7中黄色背景区域。
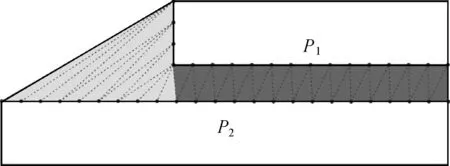
图7 有效连接区域Fig.7 Connectable area
步骤3:依据有效连接区域在整体连接区域中的面积占比计算有效连接指数(ECI)
(3)
式中,ECIXs,Xt为两邻近面状要素Xs、Xt之间的有效连接指数,CAXs,Xt、TAXs,Xt分别为两要素间的有效连接区域面积和整体连接区域面积。
由式(3)可知,当其值介于0~1之间,值越大表明邻近要素间可连接区域越大,更适宜进行毗邻化操作。根据多次试验,阈值一般设置为0.5,若ECI≥0.5,认为适宜毗邻化操作;反之,不适合。
2.1.1.3 相靠邻近特征
有效连接指数可以较好体现连续性原则,当ECI等于1时,邻近要素间的区域属于完全可连接区域,通常包括图8所示3种情况。

图8 ECI值为1的情况Fig.8 Three situations of ECI=1
然而,由图8(c)可以发现,若对短边相对邻近的两要素进行毗邻化,则不利于保持紧凑性原则。对于面要素而言,长边相对短边可以更好地概括要素的主体结构及延展方向,所以在计算有效连接指数时,若长边参与计算,则认定其相靠邻近,适宜毗邻化处理,如图8(a)、(b)所示;反之,若短边相对邻近,则认为不适宜毗邻化处理,如图8(c)所示。故本文提出投影点重叠度指数(overlap index,OI)以区分邻近要素的相靠和相对邻近两种情况。指标计算的具体步骤为:
步骤1:分别以主骨架线[16-18]代替两邻近面状要素P1、P2的长边,并相互投影,OI为面要素P1(或P2)的骨架线首末端点在面要素P2(或P1)上的两个投影点(projection point)与P2(或P1)骨架线端点的欧氏距离,见式(4)。为方便计算,本文所提投影并不是原有几何意义上的投影,而是将某一面要素主骨架线端点在另一面要素主骨架线上的最邻近点作为投影点。
(4)
式中,(x1,y1)、(x2,y2)分别为P1在P2上(或P2在P1上)的投影点p1、p2的坐标;(xi,yi)为P2(或P1)的骨架线两端点坐标,i=1,2,OI1、OI2分别为两投影点距端点pi的距离。
若OI1=OI2=0,表明面要素P1在P2上的投影点是P2主骨架线的同一个端点;若P2在P1上的投影是同样情形,说明两要素短边相对相邻。如图9所示,若P1的骨架线投影至P2,P2上骨架线的端点N3是N1、N2的最邻近点,所以它为N1、N2的投影点;同理,N2为N3、N4的投影点,此时,OI1=OI2=0,不宜毗邻化处理。
2.1.1.4 基高比率特征
面要素基高比是对其平均宽度的描述,文献[19]提出了面要素基高比计算方法
W=S/BL
(5)
式中,W为要素的近似平均宽度;S为图斑面积;BL为图斑最长长度基线,即面状要素最长骨架线的长度,如图10所示。
要素基高比及其与邻近要素之间的间距从另外视角反映了聚集性面状要素群的内部结构。当两邻近面群要素的基高比之和大于或远大于狭长桥接面间距时,毗邻化结果在保持面群要素空间分布特征不变的条件下,可以较好地突出聚集状态,适宜毗邻化处理,如图11(a)所示;当两邻近面群要素的基高比之和小于狭长桥接面间距时,若毗邻化处理会发生较大变形,此情形不适宜毗邻化,如图11(b)所示。

图9 识别短边相对邻近Fig.9 Identifying side-adjacent along short edges

图10 面要素基高比计算示意图Fig.10 Diagram of calculating the average width of area elements
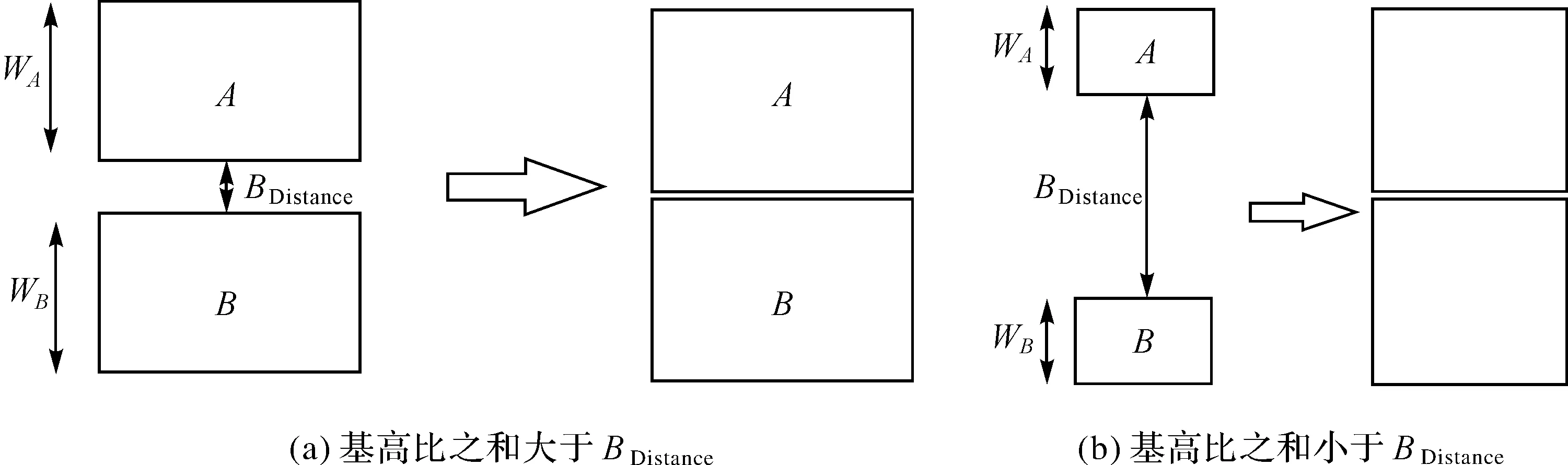
图11 相邻要素内部结构特征Fig.11 Internal structure characteristics of adjacent elements
为此,本文引入分布格局指数(distribution pattern index,DPI),反映两面要素空间主体程度及邻近度,其计算公式如下
(6)
式中,DPIXs,Xt表示空间中彼此邻近的两面状要素Xs、Xt形成的分布格局;WXs、WXt分别为要素Xs、Xt的基高比;BDistance(Xs,Xt)为要素Xs、Xt之间的间距。
主要计算步骤:①采用公式(5)计算各要素的基高比;②采用公式(2)计算两邻近面要素之间的间距(BDistance(Xs,Xt));③结合步骤①、②计算结果,利用公式(6)计算分布格局指数(DPI)。
DPIXs,Xt的值越大表明两邻近面状要素聚集性特征越强,通常情况下,该阈值设定为1。当DPIXs,Xt≥1时,适宜毗邻化操作;反之,不适宜。
2.1.2 毗邻区识别
根据上述4个特征对区域内的面状要素集{Pi}(i=1,2,…,n)进行毗邻区识别是一个迭代计算的过程,因为初始阶段识别的毗邻区极有可能成为下一阶段毗邻区的组成要素。毗邻区识别的主要步骤如下:①计算包含全部面状要素的最小面积矩形,并将其作为区域边界,构建边界约束Delaunay三角网,并计算任意两个相邻面状要素之间的平均宽度;②利用带状桥接面宽度进行毗邻区初步识别,将符合带状桥接面宽度阈值约束的相邻面要素放入候选毗邻区全集O;③按照面积由小到大的顺序对候选毗邻区全集O内的面要素进行排序,从面积最小的面要素Pi开始,依据有效连接指数(ECI)、分布格局指数(DPI)、重叠度指数(OI)约束识别适宜与其进行毗邻化操作的邻近要素,识别顺序为其邻近要素中面积最小的要素至面积最大的要素,合并识别出的所有要素,得到要素Pi所在的毗邻区Ai;④将毗邻区Ai的外围边界形成的多边形要素替换其包含的面要素,放入候选毗邻区全集O中,并更新其与各个邻近要素的宽度;⑤重复步骤③、④,探索候选毗邻区全集O内未参与识别要素所在的毗邻区,直至候选毗邻区全集O内所有要素都被处理,迭代计算识别毗邻区结束。
2.2 外围边界轮廓计算
针对现有方法在保持边界结构特征方面存在明显不足(如图2),本文引入Miter型缓冲区变换[20-21]进行外围边界轮廓计算。其主要步骤如下:
步骤1:毗邻区面群的扩张-腐蚀变换。先对原始多边形面群向外进行距离为L的数学形态学[22-23]意义上的扩张变换,以融合各个多边形扩张后重叠部分,得到边界多边形P1,如图12(b)所示,然后对多边形P1向内进行距离为L的腐蚀变换得到多边形P2,如图12(c)所示。

图12 扩张-腐蚀变换示例Fig.12 Dilation and erosion transformations
该变换具有“保凸”、“保平”、“减凹”等特点,变换前后,图形的总体形态不变,凸起和直线部分形态无变化,即“保凸”、“保平”;图形凹陷部分在变换过程中发生融合,使形态趋于光滑,即“减凹”。当然,“减凹”的强度与距离L相关。
步骤2:“补凹”。将多边形P2与原始面群统一构建拓扑,并把语义信息赋予相应弧段,若多边形中的弧段仅由某一语义及无语义信息的弧段组成,则该多边形为腐蚀变换中舍去的凹陷。那么,将具有语义信息的弧段代替无语义信息弧段以形成新的面群边界多边形P,则该多边形为毗邻区的最小包络多边形,其边界为毗邻区外围边界轮廓。如图13(a)所示,拓扑多边形O由弧段L1、L2组成,其中,L2中具有多边形D的语义信息,但因L1为P2中的弧段,因此,其不具有语义信息,由此可判定多边形O为凹部区域,将L2代替L1作为边界P的弧段,得到如图13(b)所示边界轮廓P。

图13 “补凹”过程示例Fig.13 Restore concave structure
2.3 边界约束下骨架线修正
现有研究中基于边界约束Delaunay三角网法提取的主骨架线[24-25],已可以很好地反映面要素的主延伸方向和主体形状特征,并可以有效去除桥接面汇聚处的“抖动”现象,本文针对主骨架线在边界处存在的不足(图14(a))进行修正,克服末端节点提取不准确的缺陷。主要过程如下:
首先,将桥接面与原始面群统一构建拓扑,并把语义信息赋予相应弧段,若某一弧段无语义信息且属于桥接面的组成弧段,则该弧段为边界弧段,与此弧段相连的骨架线优先得到保留;同时,若所提骨架线的末节点不在边界上,则该段骨架线应去除。由此规避骨架线末端结点未落边界的缺陷,形成适宜毗邻化线的最优骨架线。如图14(b)所示,节点A在边界L1上,因此骨架线OA得到保留;节点B在非边界的弧段L2上,因此骨架线OB应去除。
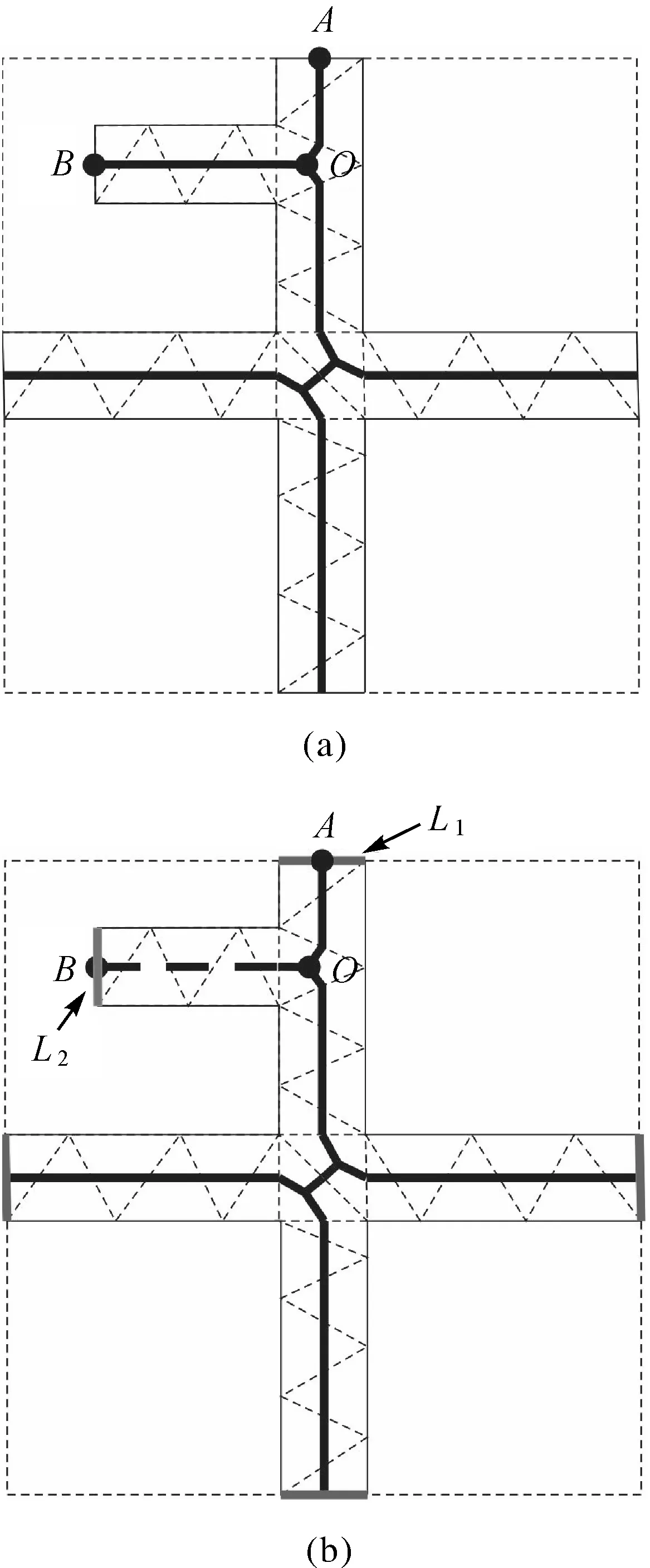
图14 骨架线修正Fig.14 Skeleton line correction
2.4 毗邻化自动处理
基于识别的毗邻区,进行毗邻化自动操作包括4步,一是计算各个毗邻区的外围边界轮廓,二是提取桥接面,三是提取桥接面毗邻化线,四是依据毗邻化线融解桥接面,其迭代计算流程如图15所示。
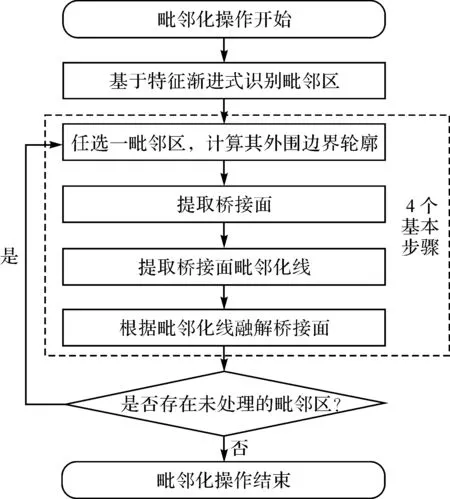
图15 毗邻化计算流程Fig.15 Calculating flow chart of agglomeration
3 试验与分析
3.1 试验数据与试验环境
依托中国测绘科学研究院研制的WJ-Ⅲ地图工作站,嵌入本文提出的毗邻区特征识别及自动处理方法,以坑塘面群为例进行合理性及效率验证。试验数据取自江苏省某市地形图数据库中的一个标准图幅,该市水产养殖发达,其内坑塘密布、形状多样,空间分布特征很有代表性。试验数据空间范围为23.91×18.67 km2,共有坑塘面要素18 559个,源比例尺1∶1万、目标比例尺1∶5万,软件系统运行环境为Windows7 64位操作系统、CPU为Intel Core I7-3770、主频3.2 GHz、内存16 GB、固态硬盘1024 GB。
本次毗邻化试验总计用时792 s。其中,毗邻区识别耗时760 s,占总用时的95.96%;毗邻化处理用时32 s。
3.2 可靠性分析
3.2.1 自动识别准确性
本次试验中,以0.4 mm作为图上的最小可视距离[26],带状桥接面宽度阈值设定为20 m,进行毗邻区自动识别与处理。本方法共自动识别出毗邻区1065个,其中,由排列规则、形状相似的面要素形成的简单毗邻区158个,占比14.83%;由形状多样、边界不规则的面要素形成的复杂毗邻区907个,占比85.17%。
为了检验毗邻区自动识别结果的可靠性和准确性,将该结果与制图专业人员人工识别出的毗邻区进行比对分析并计算叠置度。叠置度=1-[|毗邻区面积(人工识别)-毗邻区面积(自动识别)|]/毗邻区面积(人工识别)。以该叠置程度为核心指标,将识别结果区分为4种情况:第一种情况(完整符合),叠置度=100%;第二种情况(高度符合),90%≤叠置度<100%且细微差异出现在边、角处;第三种情况(一般符合),50%≤叠置度<90%且主体存在部分重叠;第四种情况(不符合),叠置度<50%。
结果对比见表1。其中,简单毗邻区符合度为98.44%,复杂毗邻区符合度86.71%。
表1毗邻化识别结果准确性比较
Tab.1Accuracycomparisonofagglomerationarearecognitionresults

毗邻区人工识别结果本文方法识别结果完全符合高度符合一般符合不符合简单毗邻区158156200复杂毗邻区886145702372
3.2.2 毗邻化效果比较
从上述自动化处理结果中,选择代表性强的毗邻区,将本文方法与传统毗邻化算法处理结果进行效果对比。对于简单毗邻区,两者处理结果基本一致,均能够较好保持原始面群的结构特征,所提毗邻化线自然延展且形态光滑,不存在抖动,如图16所示;对于复杂毗邻区,本文方法相对传统毗邻化算法,在毗邻化处理效果方面更好,如图17所示。这是由于传统方法未顾及外围边界在提取毗邻化线时的约束,边界有凹凸结构面要素的毗邻化线误提取所致,其结果与地物真实分布不一致。
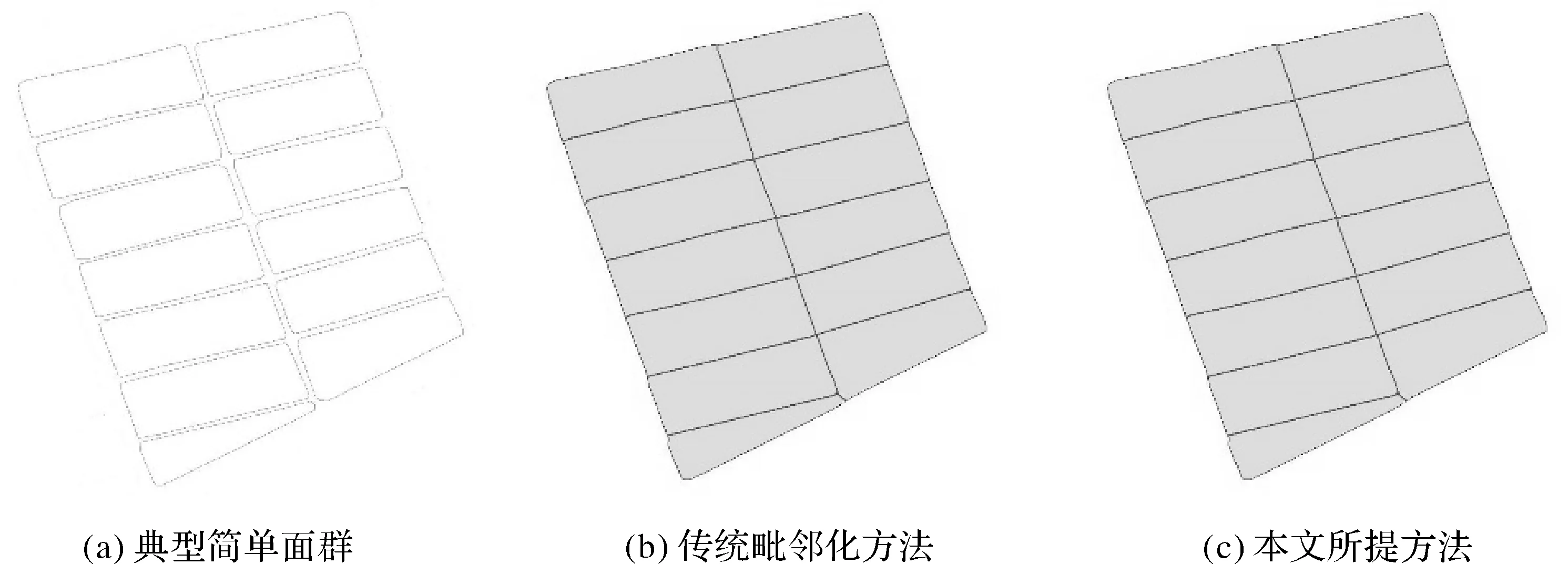
图16 简单毗邻区处理效果比较Fig.16 Comparison of processing effect in common agglomeration area
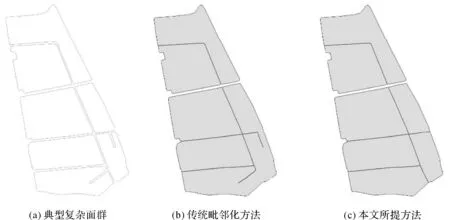
图17 复杂毗邻区处理效果比较Fig.17 Comparison of processing effect in complex agglomeration area
4 结论与讨论
针对传统毗邻化方法应用于实际地图数据时存在的毗邻区难以自动识别、复杂区域骨架线误提取等问题,本文提出了一种毗邻区自动识别及处理方法,既实现了毗邻区的自动识别,又实现了毗邻化操作的自动处理。通过实际地形图数据验证,得出结论如下:
(1) 在毗邻区识别准确性方面,本文通过1∶1万地形图一个标准图幅内的坑塘面群的毗邻化识别试验,证实简单毗邻区和复杂毗邻区自动识别结果与人工识别的符合度均达到85%以上。
(2) 在毗邻化处理效果方面,本方法不仅适用于简单毗邻区,而且对于复杂毗邻区处理结果比传统毗邻化算法更加合理。
(3) 在效率方面,本方法主要耗时于毗邻区自动识别,大致占总用时的96%。
下一步的研究重点,一是提高形态各异、分布不规律毗邻区识别准确度;二是通过主流域(如有名河流或高等级河流)对大范围面群要素进行分区,从而减少毗邻化处理的要素数量,提高毗邻化处理的效率;三是设定一定阈值对提取面群外围边界轮廓时产生的空洞进行区分,消除小面积空洞对毗邻化结果的影响。
