哨兵-2号光学影像地表形变监测:以2016年MW7.8新西兰凯库拉地震为例
2019-04-11贺礼家冯光财冯志雄
贺礼家,冯光财,冯志雄,高 华
1. 中南大学地球科学与信息物理学院雷达遥感研究室,湖南 长沙 410083; 2. 东华理工大学测绘工程学院,江西 南昌 330013
虽然光学数据易受云雾、太阳照度等因素的影响,限制了其在地表形变监测中的应用,但光学影像可以利用地表纹理信息变化快速地监测大范围、大量级的地表形变(如地震、冰川、滑坡等),并获取较高的形变监测精度。在气候条件允许下,它能很好地弥补和克服GPS技术空间分辨率低、点位覆盖稀疏以及InSAR技术易受相位失相干和最大形变梯度等限制因素影响[1-2]。
哨兵-2号(Sentinel-2)是哥白尼计划(Copernicus Programme)下多光谱成像任务中的光学卫星星座,该星座包含两颗重复轨道卫星——哨兵-2A及哨兵-2B卫星,它们分别于2015年6月和2017年3月发射升空。此前,已经有许多学者利用各种光学数据进行地表形变监测研究,如SPOT[3-9]、ASTER[10]、Landsat[11-15]以及航空影像[16-17]等。与ASTER、Landsat系列等传统的光学数据相比,哨兵-2号卫星星座具有中高空间分辨率(最高10 m)、较短重访周期(5 d)及数据免费等优势,因此在地表形变监测中的应用潜力将更加明显[18]。由于目前距哨兵-2号升空时间较短,其数据积累较少,所以目前关于它的形变监测系统误差改正和应用研究还较少,还尚未有学者对哨兵-2号影像中存在的各种系统误差源和改正方法进行系统的研究。此外,该卫星星座可以获取4个10 m空间分辨率的波段影像,何种波段更适合地表形变监测以及哨兵-2号与Landsat8两种光学遥感影像地表形变监测精度之间的差异等问题,目前还尚未有分析比较。以上内容对于哨兵-2号卫星数据的应用和推广都具有重要意义。
因此,本文首先介绍了哨兵-2号光学数据监测地表形变的数据处理流程,并分析了其影像形变场中系统误差源的组成成分及改正方法;并在传统方法的基础上,采用了改进的均值相减法以去除卫星姿态角抖动误差。另外,还对哨兵-2号影像中4个10 m空间分辨率的波段(Band 2/3/4/8)获取地表形变信息的能力进行了分析和比较,通过对不同波段影像获取的形变结果进行精度评定,选取和验证了地表形变监测的最佳波段。接着,分别利用哨兵-2号和Landsat8影像获取了2016年11月14日MW7.8新西兰凯库拉地震的同震形变场,并对两种光学影像的观测结果进行了对比分析。最后,本文总结了哨兵-2号光学影像中的系统误差源去除方法和精度分析,展望了该数据在地表形变监测中的应用前景。
1 系统误差改正
1.1 数据介绍
哨兵-2号多光谱成像仪(MSI)采用推扫式成像模式,该卫星星座含13个通道,其中10个通道是波长为433~955 nm的可见光近红外谱段(VNIR),其他3个通道是波长为1360~2280 nm的短波红外谱段(SWIR)。哨兵-2号卫星的成像幅宽为290 km,光谱分辨率为15~180 nm,空间分辨率包括10、20和60 m。本文采用4个10 m空间分辨率的可见光近红外波段影像(Band 2/3/4/8)进行试验分析,这4个光谱波段的光谱和辐射信息见表1。
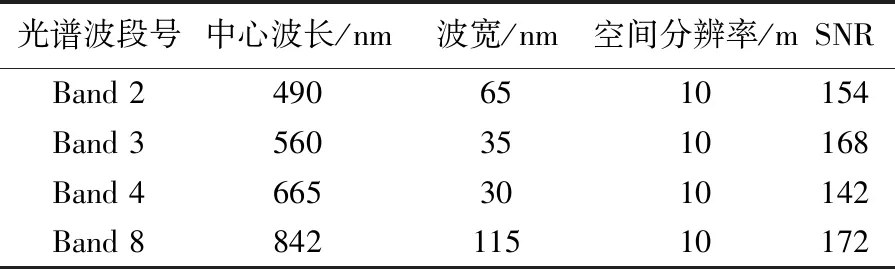
表1 哨兵-2号光学影像光谱波段信息简介
1.2 数据处理
本文选取新西兰东北部凯库拉县(Kaikoura)为研究区域(如图1所示)。该区域在2016年11月14日发生了MW7.8级大地震。该研究区域地形地貌丰富,地表破裂明显,非常适合利用哨兵-2号光学数据进行系统误差分析和同震形变监测研究。本文从美国地质调查局(United States Geological Survey,USGS)收集了哨兵-2号震前数据2景,震后数据15景,详细数据信息见表2。此外,为了验证和比较哨兵-2号影像获得的形变结果,本文也收集了同时期的两景Landsat8影像。如图2所示,这17景哨兵-2号影像可构成10对时间间隔均为10 d的震后影像对组合,这些影像对获取的形变场中均存在各种系统误差源。本文利用COSI-Corr软件包[19-20]和交叉频谱相关算法[9,21-22]获取了地表形变场,然后选取了系统误差比较明显的两个影像对2016-12-15—2016-12-25及2016-12-25—2017-01-04(Band8影像),对形变场中的各种系统误差源进行系统分析。
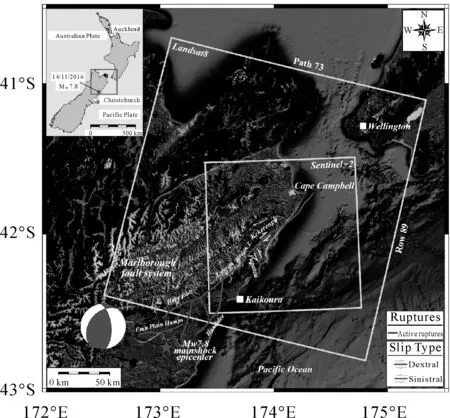
图1 2016年MW7.8新西兰凯库拉地震构造背景图Fig.1 Tectonic setting of 2016 MW7.8 Kaikoura, New Zealand earthquake

图2 哨兵-2号相关影像对采集日期分布Fig.2 Acquisition dates of the Sentinel-2 correlation image pairs
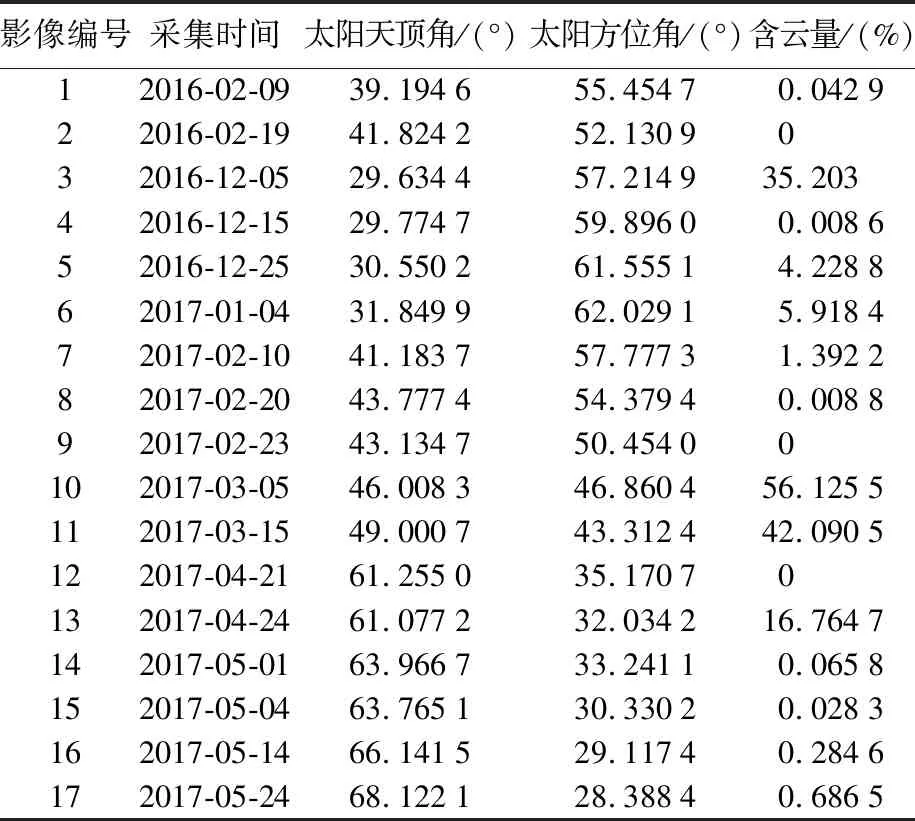
影像编号采集时间太阳天顶角/(°)太阳方位角/(°)含云量/(%)12016-02-0939.194655.45470.042922016-02-1941.824252.1309032016-12-0529.634457.214935.20342016-12-1529.774759.89600.008652016-12-2530.550261.55514.228862017-01-0431.849962.02915.918472017-02-1041.183757.77731.392282017-02-2043.777454.37940.008892017-02-2343.134750.45400102017-03-0546.008346.860456.1255112017-03-1549.000743.312442.0905122017-04-2161.255035.17070132017-04-2461.077232.034216.7647142017-05-0163.966733.24110.0658152017-05-0463.765130.33020.0283162017-05-1466.141529.11740.2846172017-05-2468.122128.38840.6865
光学影像地表形变监测完整的数据处理流程(如图3所示),主要包括如下4个步骤:
(1) 数据预处理:由于哨兵-2号数据与Landsat8数据的影像覆盖范围存在差异,为方便对两类数据结果进行对比分析,需要对这两类影像进行裁剪。
(2) 相关性计算:以COSI-Corr为数据处理平台,对影像对进行亚像素的相关性匹配(sub-pixel correlation)计算[23-24]。对于哨兵-2号数据,参数设置如下:搜索窗口大小为32×32像素(地面分辨率约为320×320 m);移动步长为8×8像素(地面分辨率为80×80 m);掩膜阈值为0.9;迭代次数为2次。
(3) 误差后处理:为了去除二维形变场中的各种系统误差源,需要进行误差后处理。依次去除失相关噪声、轨道误差、条带误差等,最后再通过3×3像素的中值滤波窗口进一步降噪[25]。
(4) 形变值重采样:为方便GMT(generic mapping tools)绘图和不同类型数据比较,需要进行坐标转换。对UTM坐标系下获取的二维形变场中的形变值进行重采样,得到WGS-84坐标系下的二维形变场。

图3 光学影像地表形变监测数据处理流程Fig.3 Flow chart of processing the ground deformation obtained from optical images
1.3 误差分析及纠正
本文以哨兵-2号2016-12-15—2016-12-25震后影像对为例,通过相关性计算获取了新西兰地震覆盖区域的东西向和南北向二维地表形变场(如图4所示)。通过分析发现哨兵-2号光学影像获取的形变场中主要存在以下几种系统误差源:失相关噪声、轨道误差、条带误差以及卫星姿态角误差等(如图4所示)。此外,光学影像形变场中一般存在地形阴影误差[16],但是考虑到地形阴影误差的复杂性,本文不予分析。后文将针对上述各种系统误差的分布特点、产生原因以及去除方法进行系统性分析。
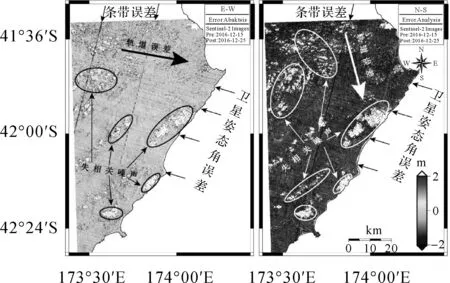
注:影像形变场处于WGS-84坐标系,分别以朝东和朝北方向为形变值的正方向。图4 哨兵-2号影像对(2016-12-15—2016-12-25)东西向和南北向影像形变场系统误差源Fig.4 System error sources in the EW and NS components of the image deformation field from the (2016-12-15—2016-12-25) image pair
1.3.1 失相关噪声
失相关噪声与地表辐射性能息息相关。当地表辐射性能变化较小时,可能会使影像的纹理特征产生微小变化;而当辐射性能变化较大时,则会引起影像纹理的缺失。失相关噪声水平可用信噪比值(SNR)进行描述。当影像中某个区域的信噪比值普遍较低时,该区域可能受失相关噪声的影响[9,16]。失相关噪声产生的原因可归纳为如下几点:
(1) 时间失相关。自然因素:云、雪、植被、水域等覆盖区域的变化;人为因素:新增建筑物等。
(2) 地形阴影。同一传感器在不同季节采集的影像对应的太阳角(包括太阳高度角和方位角)不同会使形变场中某些区域产生地形阴影。
由于失相关噪声的存在,通过对影像进行窗口匹配不仅难以取得好的相关性计算结果,而且还会大大降低形变值的测量精度。为了降低失相关噪声的影响,一般采用如下两种解决方案:
(1) 程序自动掩膜掉形变场中SNR低于某阈值(经验值取0.9)的区域。
(2) 人为掩膜掉由云、雪、植被等因素引起的范围较大的失相关区域。
1.3.2 轨道误差
虽然从USGS上下载的哨兵-2号L1C级数据是正射产品,但是该数据没有经过严格的正射校正和几何校正,因此通过相关性计算得到的影像形变场中依然存在明显的线性长波长误差,即轨道误差。本文以哨兵-2号2016-12-25—2017-01-04影像对为例,利用一次多项式曲面拟合模型去除轨道误差[26-29]。计算公式如下
φorbit=a0+a1x+a2y+a3xy
(1)
其中,φorbit为轨道趋势项误差;x为距离向坐标;y为方位向坐标;a0、a1、a2、a3为待求参数,可根据最小二乘平差原理求解。具体步骤为:首先在形变场中远离地表破裂带的非形变区域均匀的选取若干像素点,根据这些点的图像坐标及形变值建立多项式误差曲面以计算待求系数a0、a1、a2、a3,然后根据这些参数模拟整个形变场的轨道趋势面,从而获得去除轨道误差的形变场。如图5所示,为轨道误差去除前后的对比图,哨兵-2号东西向和南北向影像形变场中轨道误差变化缓慢,以常数为主。

图5 哨兵-2号影像对(2016-12-25—2017-01-04)东西向和南北向影像形变场中轨道误差去除前后对比Fig.5 Before and after removing the orbital errors in the EW and NS components of the image deformation field from the Sentinel-2 image pair (2016-12-25—2017-01-04)
1.3.3 条带误差
对于大多数推扫式成像卫星(如SPOT系列、Landsat系列、ASTER等)而言,沿轨道方向都会产生明显且均匀分布的线性信号,该信号即条带误差。条带误差产生的原因可归纳为如下两点:
(1) 正射影像在内定向时没有经过合理的建模,使得多光谱仪器探测器中的CCD(charge coupled device,电耦合器件)线阵列错位排列[16,30]。
(2) CCD线阵列抖动引起的误差没有通过建模消除。相邻且交错排列的CCD线阵列振动会使采集的影像产生偏移,其偏移量大小取决于CCD阵列振动的频率、振幅及相邻CCD阵列对同一地理位置成像的时间间隔[31]。
为了消除CCD线阵列引起的条带误差,本文采用传统的“均值相减法”去除条带误差[1,16]。本文选用哨兵-2号2016-12-25—2017-01-04震后影像对进行计算分析,这不仅能保证良好的相干性又可以避免同震形变的干扰。条带误差去除的具体流程如图6所示,结果如图7所示。
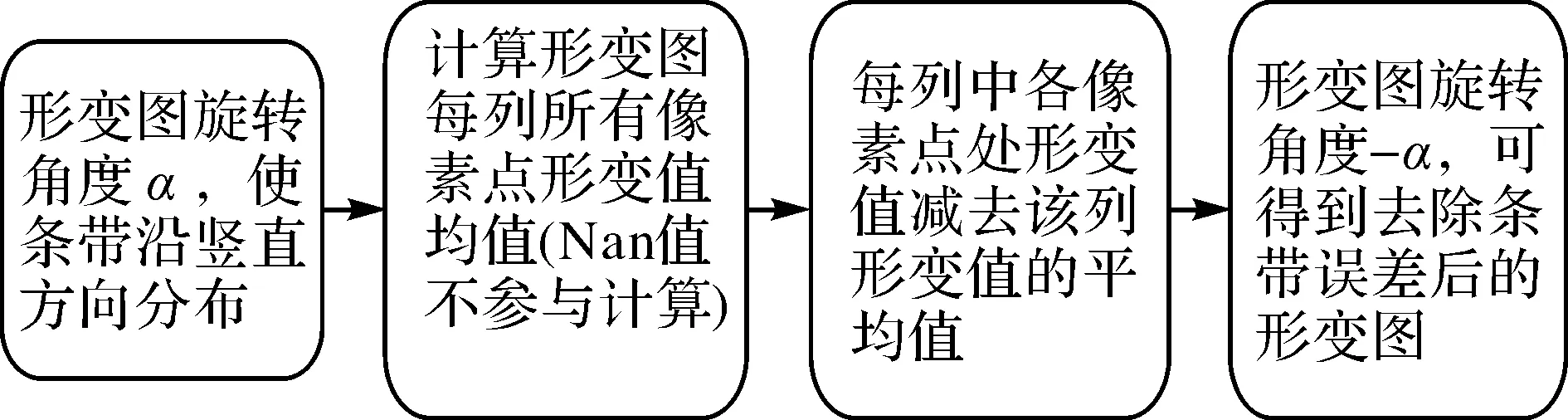
图6 均值相减法去除条带误差数据处理流程Fig.6 Flow chart of removing the stripe artifact using the mean subtracting method
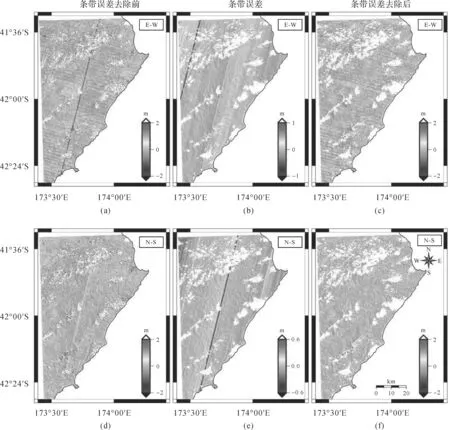
图7 哨兵-2号影像对(2016-12-25—2017-01-04)东西向和南北向影像形变场中条带误差去除前后对比Fig.7 Before and after removing the stripe artifact in the E-W and N-S components of the image deformation field from the Sentinel-2 image pair (2016-12-25—2017-01-04)
1.3.4 卫星姿态角误差
在形变场中,沿交叉轨道方向呈现出周期性均匀平行分布的带状信号,即卫星姿态角抖动误差。该误差产生的原因可归纳如下:
(1) 在影像采集过程中,航天器振动引起的误差没有通过建模消除[31]。
(2) 在影像正射校正过程中,由于卫星姿态角欠采样,导致无法精确计算卫星姿态角[32]。
(3) 在东西向形变图中,该误差主要是由未被记录的roll角变化引起,在南北向形变图中,该误差主要是由未被记录的pitch角变化引起[1,9,32]。
为了去除形变场中卫星姿态角抖动引起的误差,传统采用与去除条带误差相同的方法(均值相减法)。但是本文考虑到沿卫星交叉轨道方向地形起伏变化、植被覆盖等因素的影响,沿卫星交叉轨道方向的卫星姿态角误差是变化而非固定不变的,直接采用传统方法并不能取得良好的误差去除效果。因此,本文结合哨兵-2号卫星推扫式成像仪焦平面上共有12个交错排列的CCD线阵列探测器的特点,提出改进后的“均值相减法”去除卫星姿态角误差。该改进方法的主要思想为:首先定义一个量η用于定量的衡量形变场中的卫星姿态角误差水平,可表示为
(2)
式中,m、n分别表示形变图的最大行数、最大列数;a、b分别表示形变图中某行第j等份中始端、末端像素点的位置参数;r表示将形变图每行所含像素点总数均分成12等份;D表示某一像素点位的形变值;ceil(·)函数用于求取大于某一数值的最小整数。采用该改进的方法后,误差的去除效果有很大的提升(如图9所示),而且与传统方法相比计算的复杂程度并没有太大的增加。本文以哨兵-2号2016-12-25—2017-01-04影像对为例,利用改进后的均值相减法去除卫星姿态角误差,具体的处理流程如图8所示,结果如图9所示。
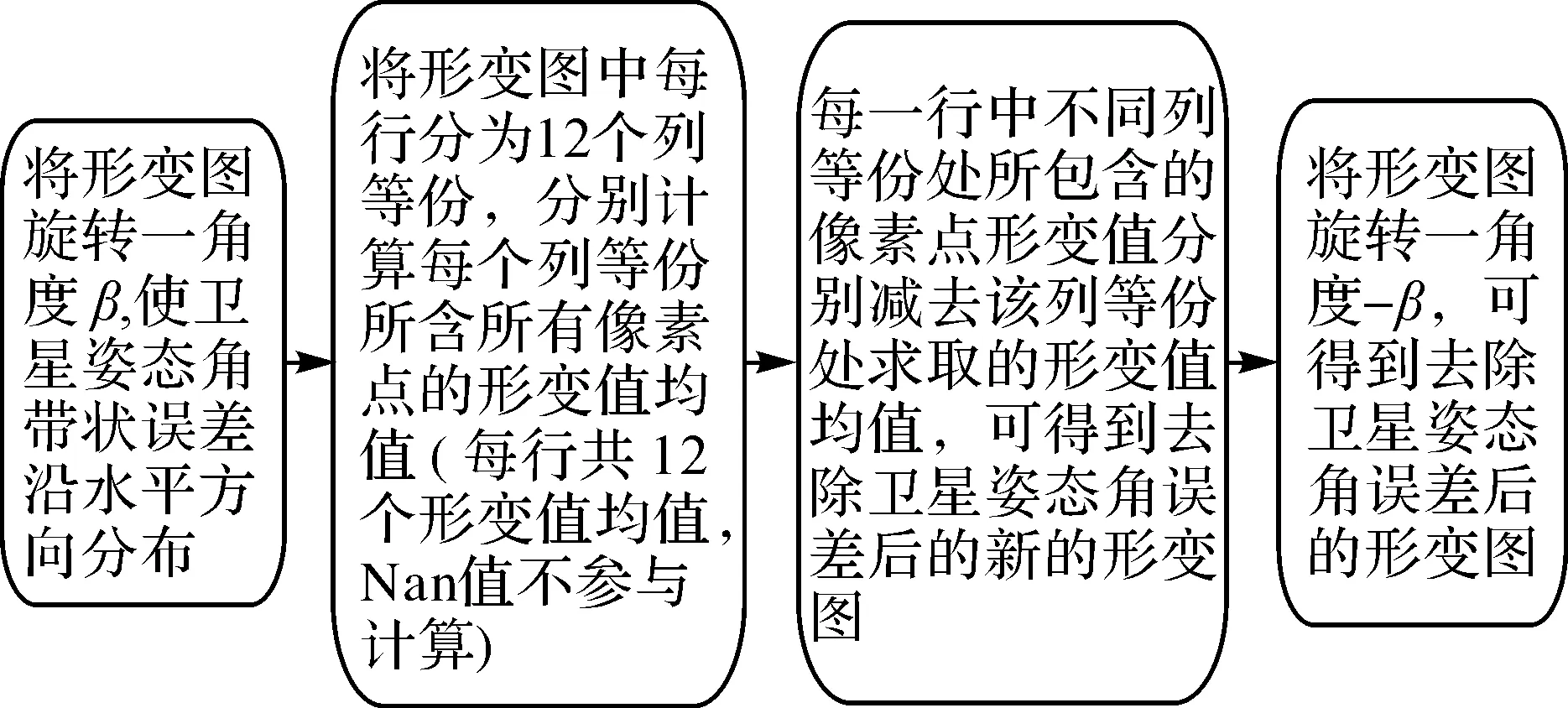
图8 改进后的均值相减法去除卫星姿态角误差数据处理流程Fig.8 Flow chart of removing the satellite attitude jitter distortion using the modified mean subtracting method
2 最佳波段分析
2.1 数据处理
哨兵-2号光学影像中共有4个10 m空间分辨率的可见光近红外波段(Band 2/3/4/8)。虽然这4个光谱波段具有相同的空间分辨率,但是其波段宽度、SNR值以及辐射特性却不尽相同[33],详见表1。本文利用10对哨兵-2号震后影像对(如图2所示)对应的4波段影像数据进行试验分析。由于这些震后影像对的时间基线较短(10 d),地表一般不会发生明显的形变。因此,通过分析不同波段影像获取的影像形变场中形变值的误差水平,可以反映出不同波段影像地表形变监测能力的差异。本文利用4个不同波段的影像对组合进行地表形变监测的最佳波段选取分析。具体的数据处理流程主要包括以下2个步骤:
(1) 相关性计算:利用COSI-Corr分别计算不同波段(Band 2/3/4/8)对应的10个相关性影像对(如图2所示)的二维地表形变场。计算参数统一为:搜索窗口大小为32×32像素;移动步长为8×8像素;掩膜阈值为0.9;迭代次数为2次。
(2) 误差后处理:采用上一节介绍的系统误差源改正方法,依次去除影像形变场中的各种系统误差源(失相关噪声、轨道误差、条带误差、卫星姿态角误差等),再通过3×3的中值滤波窗口进一步降噪。
在经过以上步骤后,本文对获得的形变值的平均值和标准差进行统计分析。统计结果显示不同波段影像获取的影像形变场中形变值的均值均接近于0 m,这表明图2中这些震后影像对的形变场受余震形变影响较小。因此,本文主要对不同波段获取的形变场中形变值的标准差进行对比分析,统计数据见表3和图10。值得注意的是,在统计形变值标准差时,本文将形变值为空值(Nan)以及形变值绝对值较大的异常值不参与统计。
2.2 精度评定
本文以整个影像形变场中形变值的标准差作为精度评价指标。由表3中的统计数据可知,在哨兵-2号10个影像对形变场中,无论是东西向还是南北向形变场,Band 8的标准差均表现为最小,其余波段获取的影像形变场中形变值标准差的统计结果没有明显的差异。统计结果表明:就该试验区域而言,哨兵-2号4个10 m空间分辨率波段中,第8波段(Band 8)影像是地表形变监测的最佳波段。另外,哨兵-2号4个可见光近红外波段的光谱辐射性能中,第8波段的波段宽度最宽(115 nm),信噪比值SNR最大(172)(见表1),这也进一步间接地验证了本文试验结论。

图9 哨兵-2号影像对(2016-12-25—2017-01-04)东西向和南北向影像形变场中卫星姿态角误差去除前后对比Fig.9 Before and after removing the satellite attitude jitter distortion in the EW and NS components of image deformation field from the Sentinel-2 image pair (2016-12-25—2017-01-04)

标准差/m影像对编号东西向(E-W)南北向(N-S)Band 2Band 3Band 4Band 8Band 2Band 3Band 4Band 810.4170.390.3710.3340.4020.3770.3580.32620.4280.4080.4030.3640.410.3930.3890.35930.4370.420.4020.3690.4140.3990.3790.35740.4190.3750.3620.3310.4230.3950.3750.37450.4760.4440.4310.3920.4810.4610.4440.42260.4710.4350.4250.3990.4810.4650.4540.44670.4950.4650.4560.4210.4920.4710.4630.44180.4850.4450.4350.4010.4850.4630.4540.44190.4220.4060.3910.3760.4120.3980.3830.383100.4990.4750.470.4440.4880.4720.4620.447平均值0.4540.4260.4140.3830.4490.4290.4160.400
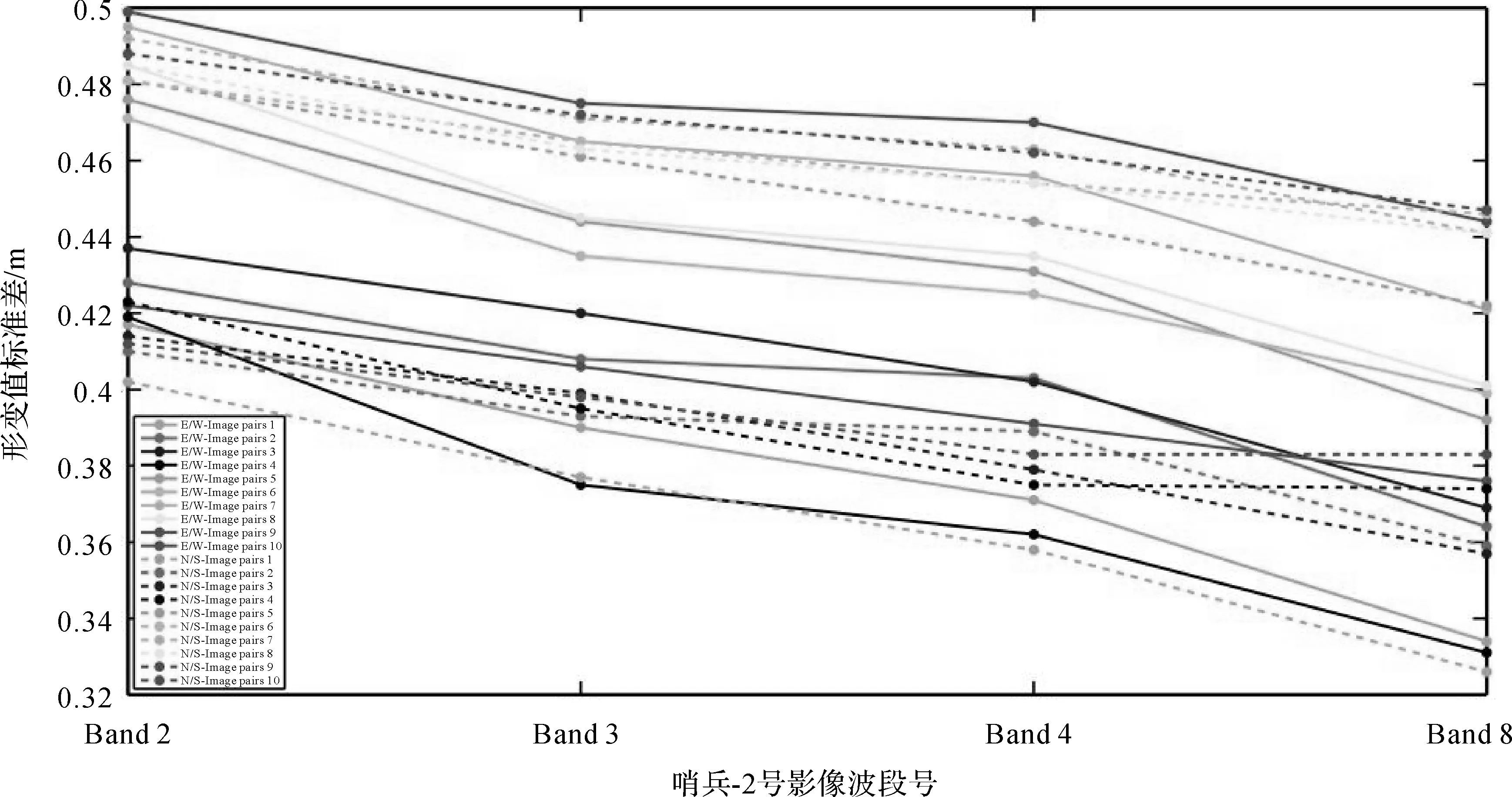
图10 形变值标准差统计Fig.10 The displacement standard deviation diagram
3 新西兰凯库拉Mw7.8地震同震形变监测
3.1 地震简介
2016年11月14日凌晨2时56分,新西兰境内凯库拉镇(Kaikoura)发生Mw7.8大地震,此次地震是该地区150多年来发生的强度最大的地震。根据USGS给出的震源机制解,该地震震中位于42.737°S,173.054°E,距离凯库拉镇西南方向约60 km,震源深度约为15 km;该地震是一个以右旋走滑为主兼少许逆冲分量的地震。该地震地表破裂始于Hope断层,之后依次沿着Jordan thrust、Papatea及Kekerengu[34-36]等主要断层向东北方向传播。此次地震的地表破裂总长超过150 km,沿Needles断层的近海地表破裂长度约为34 km(如图1所示)。
3.2 数据处理
本文利用以上数据处理方法和哨兵-2号影像获取2016年11月14日Mw7.8新西兰凯库拉地震的东西向和南北向同震形变场,具体的数据处理流程如图3所示。本文选用的哨兵-2号数据见表4,这两景数据覆盖了整个地震破裂带区域(如图2所示),含云量小于1%,时间间隔约为1 a,太阳照度和数据相干性得到了良好的保障,极大地减少了地形阴影误差和时间失相关噪声对形变结果的影响[15]。另外为了对地震形变结果进行对比分析和交叉验证,本研究采用“小空间基线法”[16]选取了地震前后15 m空间分辨率的Landsat8全色影像(Band 8)各1景(见表4),两景影像采集于相同的季节,含云量较低,时间间隔也约为1 a。
表4同震形变监测光学影像参数表
Tab.4Parametersoftheopticalimagesforthecoseismicdisplacementsmonitoring

卫星波段影像采集时间含云量/(%)震前震后震前震后时间间隔/dSentinel-2Band 82016-02-192017-02-2300370Landsat8Band 82015-12-132016-12-154.766.76368
为了让哨兵-2号和Landsat8数据能获取相似分辨率的同震形变结果,本文的计算参数设置如下:搜索窗口的大小均设置为32×32像素(对应地面分辨率:哨兵-2号为320×320 m,Landsat8为480×480 m);移动步长:哨兵-2号设置为9×9像素,Landsat8设置为6×6像素(对应地面分辨率均为90 m);掩膜阈值均为0.9;迭代次数均为2次。通过以上相关性计算获取的形变场中包含了各种系统误差源(失相关噪声、轨道误差、条带误差、卫星姿态角误差等),因此需要对上述同震形变结果进行误差后处理,本文采用第2章介绍的方法去除哨兵-2号和Landsat8形变场中的各种系统误差。由于上述Landsat8形变场中没有明显的条带误差及卫星姿态角误差,因此本文只采用一次多项式曲面模型去除其形变场中的轨道误差。最后,本文采用3×3像素大小的中值滤波窗口对哨兵-2号和Landsat8的结果进行进一步降噪。
3.3 结果比较分析
如图11所示,此次地震的地表破裂带主要发生在Kekerengu、Jordan thrust及Papatea断层。其中Kekerengu断层(右旋走滑)的地表形变并非对称分布,该断层上盘(NW)形变明显大于下盘(SE),这说明Kekerengu断层向北方向倾斜,该断层水平方向的最大水平滑移量为9~10 m。Jordan thrust断层(右旋走滑)的最大水平滑移量约为3 m。位于Kekerengu断层南部以及Jordan thrust断层东南方向存在一个与这两个断层相交的Papatea断层,该断层此前是一个未知的活跃断层,该断层滑动兼具左旋走滑(最大水平滑移量约4 m),位于Clarence河西南方向约20 km处。此外,在Marlborough断层系统中,沿西南方向的主要断层(如Jordan thrust等)的地表破裂长度以及最大水平滑移量均明显的小于东北方向的主要断层(如Kekerengu断层等)。如图11中近断裂带区域A,D(哨兵-2号)及区域B,E(Landsat8)对比所示,与Landsat8相比,整个哨兵-2号影像形变场中异常值(Nan值)更少,在近场区域尤为明显。图11(c)、(f)分别为哨兵-2号与Landsat8的东西向和南北向形变场差值图,其形变值的均值在近场(区域C、F)和远场区域(近场以外的形变区域)均较为接近。其中近场区域东西向形变值差值的均值约为0.1 m,南北向约为-0.2 m;而远场区域东西向形变值差值的均值约为0.2 m,南北向约为-0.1 m。但是形变值差值的均方差(RMSE)在近场和远场区域有一定的差异,其中近场区域的RMSE约为0.6 m,而远场区域的RMSE约为1.1 m。这种差异可能是因为近场地形起伏较小、植被覆盖较少,从而使得光学影像形变监测信噪比较高,而远场山区地形更加复杂,植被也更为茂盛,所以信噪比较低。根据COSI-Corr软件基于亚像素的相关性匹配算法用来探测同震形变(近场)的匹配精度一般可达1/20个像素[7],即理论上哨兵-2号和Landsat8的同震形变监测精度最高分别可以达到0.5 m和0.75 m,这表明本文所计算的精度水平(RMSE)较为合理。
总体来说,在近场区域哨兵-2号影像的同震形变监测结果与Landsat8影像的形变结果有较好的一致性,但是哨兵-2号的形变图更加清晰且形变结果中的异常值更少。如图12所示,为哨兵-2号与Landsat8地震形变结果的中误差,结果同样表明哨兵-2号同震形变结果的精度明显优于Landsat8影像,这可能与哨兵-2号数据具有更高的时空分辨率密切相关。
4 结 论
本文以新西兰地震覆盖区域为例,对哨兵-2号影像形变场中各种系统误差源的时空分布特征及误差去除方法进行了系统分析,并且创新地提出了改进的均值相减法对形变场中的卫星姿态角抖动误差进行有效去除。在误差分析的基础上,还对哨兵-2号影像4个10 m空间分辨率的波段(Band 2/3/4/8)获取地表形变信息的能力进行了统计分析及精度评定,统计结果揭示了Band8为地表形变监测的最佳波段。最后利用时间间隔均约为1年的哨兵-2号和Landsat8影像对,获取了2016年11月14日MW7.8新西兰凯库拉地震的同震形变场。形变监测结果表明:地表滑动主要集中在Kekerengu、Papatea及Jordan Thrust断层,其中沿Kekerengu断层的最大水平滑移量为9~10 m,沿Papatea断层的最大水平滑移量为3~4 m,沿Jordan Thrust断层的最大水平滑移量约为3 m。另外,两种光学数据的形变结果比较表明:虽然在近场哨兵-2号与Landsat8的同震形变结果一致性较好,但是在整个影像中,与Landsat8相比,哨兵-2号获取的形变结果异常值更少,形变图更清晰,中误差更小。因此,哨兵-2号数据可以很好地弥补其他数据在空间分辨率和时间分辨率上的缺口,为防震减灾工作的开展提供一个很好的数据平台。
致谢:本研究所用的哨兵-2号和Landsat8数据来源于USGS(glovis.usgs.gov/),文中主要采用GMT5.2.1软件绘制各种图形,采用美国加州理工学院研发的软件包COSI-Corr(http:∥www.tectonics.caltech.edu)进行数据处理。

图11 哨兵-2号影像对(2016-02-19—2017-02-23)和Landsat8影像对(2015-12-13—2016-12-15)分别获取的2016年11月14日Mw7.8新西兰凯库拉地震的同震形变场Fig.11 Coseismic deformation fields obtained by Sentinel-2 (2016-02-19—2017-02-23) and Landsat8 (2015-12-13—2016-12-15)
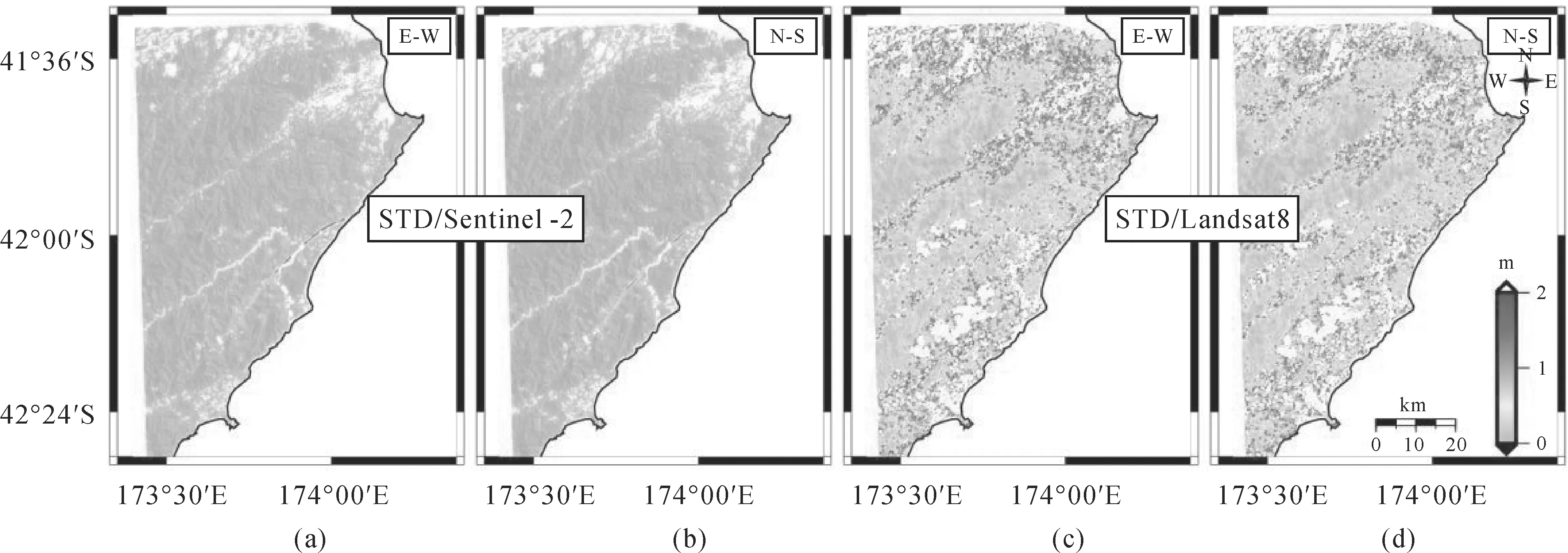
图12 新西兰地震形变场形变值中误差统计Fig.12 The displacement standard deviation of the New Zealand earthquake deformation field
