海上距离元胞自动机分析法
2019-04-11王加胜朱彦辉熊建红
王加胜,杨 昆,朱彦辉,熊建红
1. 云南师范大学信息学院,云南 昆明 650500; 2. 西部资源环境地理信息技术教育部工程研究中心,云南 昆明 650500
距离变换最早由Rosenfeld和Pfaltz提出,是指将每个栅格像元映射为到最近感兴趣区域或目标区域的距离,其输入图像一般为二值图像[1]。其中的距离一般为欧氏距离。由于根据定义计算复杂度较高,文献[2]提出了一种距离变换的快速实现算法——楔形距离变换。该方法仅考虑邻域像元的影响,通过两次扫描完成距离变换。该算法速度快,但无法得到精确的结果。此后,许多学者通过改变邻域大小和优化距离算子提高楔形距离变换精度[3-6]。
2004年,文献[7]将距离变换引入到GIS中,讨论了距离变换在GIS领域的应用场景。目前距离变换已成为GIS中的一个基本工具[8-12]。在GIS邻域距离变换的许多应用场景中,常常需要考虑障碍区域的影响,计算非障碍栅格像元到最近目标最短路径长度(如航线设计、海上救助等)[13-16]。这种距离变换,本文称之为绕障欧氏距离变换。目前,未见有专门针对绕障距离变换的研究。
元胞自动机(cellular automata,CA)是一种时间和空间都离散的动力学系统[17],广泛应用于城市规划[18-19]、土地利用[10]、传染病传播[20]、交通系统[21]、人群疏散等领域[22-24]。例如,文献[25]构建元胞自动机模型,分析了个体行为对人群疏散效果的影响;文献[26]将元胞自动机与系统生物学结合研究癌症病毒的演化过程;文献[27]集成CA与随机森林方法模拟城市扩张过程;文献[28]构建了城市和区域规划元胞自动机模型。
元胞自动机的元胞与栅格数据的像元有相似之处,距离变换可以离散成为由目标像元向外扩散和更新绕障距离值的过程,因此可用元胞状态变化来反映距离变换过程。文献[29]提出了一种基于元胞自动机的栅格空间复杂实体加权距离变换方法,但未考虑障碍的影响。本文拟提出一种基于元胞自动机的绕障距离变换方法,并以南海及邻近海域为例,分析该方法计算结果的精度与适用性。
1 研究区与数据
1.1 研究区
本文选择南海及其邻域作为研究区(0°N—24°N,98°E—122°E),以测试方法的精度与适用性。南海及邻域位于亚洲东南部,海域包括南海和泰国湾的全部,苏禄海和苏拉威西海的一部分,以及马六甲海峡、台湾海峡、巴士海峡等众多海峡,是太平洋与印度洋的连接地带。陆地涉及中国南部沿海、南海诸岛、中南半岛、菲律宾群岛和大巽他群岛。该区域岛礁众多,大小不一,陆地海岸线狭长复杂,这些特性为分析绕障欧氏距离变换结果提供了良好的测试环境。
1.2 数据及预处理
本文使用的数据资料包括陆地岛礁图层和目标点图层。陆地岛礁图层使用中国及东南亚的行政区划Shapefile矢量数据,通过国家地理信息公共服务平台服务资源中全球矢量地图服务中对南海及邻域矢量化陆地范围得到,比例尺为1∶1000万,坐标系统为2000国家大地坐标系。目标点图层通过在研究区海域随机选取7个点,用于分组测试不同数量目标情况下绕障欧氏距离变换效果。
距离分析需在投影坐标系统下进行。在导入模型前,将数据转换为Lambert-等角圆锥投影坐标系统,标准纬线为6°N与18°N,中央经线为110°E,单位为千米。由于距离变换结果用栅格表示,需要将投影转换后的行政区划图层转换为栅格图层(像元大小为5 km),1表示陆地或岛礁(即障碍区),0表示水域(正常区域),转换后的栅格大小为500×500。同时将目标点位置处的栅格值设置为2。处理后的栅格在此称为元胞的环境栅格。
2 研究方法
2.1 基本概念
在介绍模型之前,有必要对文中涉及的欧氏距离、欧氏距离变换、绕障欧氏距离变换、元胞自动机等基本概念予以明确。假设二值栅格图像尺寸为m×n,Ci(xi,yi)、Cj(xj,yj)为图像中的任意两像元。O为目标像元集合,B为障碍像元集合。
(1) 欧氏距离D(Ci,Cj)。用两点坐标差值平方和的平方根表示,即
(1)
(2) 欧氏距离变换。变换的结果使得每个像元值为该像元至最近目标点的欧氏距离。设像元p的欧氏距离变换值用DT(p)表示。q为O中的任意一像元。则欧氏距离变换可由式(2)表示
DT(p)=min{D(p,q),q∈O}
(2)
(3) 绕障欧氏距离。表示任一非障碍集像元经过非障碍区到达最近目标像元最短路径的长度。
(4) 绕障欧氏距离变换。变换结果使得任一非障碍集像元值为该像元到目标像元集的绕障欧氏距离。设Lm(p…q)表示从p经过非障碍区到q路径的最小长度。像元p的绕障欧氏距离变换可表示为
EDT(p)=min{Lm(p…q),q∈O}
(3)

D(Ck,p)}
(4)
式中,C1,Ci,Ck∉B。
(5) 元胞自动机。元胞自动机是一种时间、空间、状态都离散,空间相互作用和时间因果关系都为局部的网格动力学模型,具有复杂系统时空演化过程的能力。每一元胞取有限的状态、遵循同样的规则、通过简单的相互作用构成动态系统的演化。元胞自动机可用一个四元组描述。A={Ld,S,N,f},其中Ld标识d维元胞空间;S为元胞有限状态;N为邻域元胞集合;f表示中心元胞的状态转换规则。
2.2 绕障欧氏距离变换CA模型
CA模型的关键在于元胞与状态转换规则的定义。在传统的元胞自动机模型中,元胞的状态是有限的整数。本文将元胞状态定义为实数类型,以模拟距离变换计算过程。绕障欧氏距离变换元胞自动机模型架构如图1所示,包括模型初始化、元胞状态转换、模型表达与输出3个部分。

图1 距离分析元胞自动机模型架构Fig.1 The technique route of distance analysis CA model
2.2.1 元胞定义
将研究区根据像元大小(栅格分辨率,用Sc表示)划分为m×n正方形格网,每个单元即为一个元胞。本文将元胞的状态定义为元胞中心位置至目标点集的绕障欧氏距离(格数),用dt表示。此外,元胞还具有位置(即所在列x,所在行y)、状态变化标志(fs),障碍区标志(fl)两个属性。位置为(x,y)元胞表示为C(x,y)。元胞属性的具体描述见表1。

表1 元胞属性说明
2.2.2 模型初始化
模型初始化即模型运行前的元胞属性初始化与参数设置。模型的参数包括环境栅格和像元大小Sc。读入环境栅格数据后赋予元胞的障碍标志属性fl。Sc可以根据实际要求的精度确定,影响着元胞的大小与数量;状态dt的初始值分为两种情况,目标点所在元胞状态dt设为0,其余元胞为+∞(比最大距离大的数,如w×h);状态变化标志ft设置为0;x、y则根据元胞位置确定。元胞的属性中fl、x、y初始化后并不会改变。
2.2.3 元胞状态转换
元胞状态转换是整个模型的核心,根据相邻元胞的状态,计算当前元胞的状态。距离计算过程可以看作由目标像元向周围逐渐扩散的过程,目标与周围的8个像元的距离可根据欧氏距离计算得出,再加上周围元胞的最小状态值,即可得到元胞的状态。本文每个时刻的元胞状态转换就是更新元胞距离值。状态转换涉及邻域定义和转换规则。
(1) 邻域。本文采用邻近的8个元胞表示当前元胞的邻域,即元胞C(x,y)的邻域元胞有C(x-1,y-1)、C(1,y-1)、C(x+1,y-1)、C(x-1,y)、C(x+1,y)、C(x-1,y+1)、C(x+1,y)、C(x+1,y+1)。
(2) 状态转换规则:
陆域元胞:不进行状态转换。
邻域皆未计算的元胞:不进行状态转换。
其他元胞:设其与邻域状态(至目标最短路径长度)组成的3×3矩阵为Dt,邻域至中心元胞距离的3×3矩阵为A(称为距离算子,具有中心对称性,中心为0)。元胞下一状态值(至目标最短路径长度)即为矩阵Dt+A的最小元素值。这一规则转化过程可用式(5)—式(7)表示
(5)
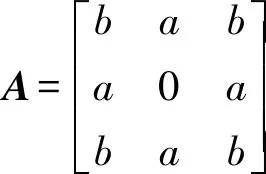
(6)
dt+1=min(Dt+A)
(7)
距离算子的选择会影响到变换的精度和速度。在楔形距离变换中,常见的距离算子及其最大绝对错误率见表2。其中最小的距离算子为Butt-Maragos优化算子。本文使用该算子距离变换。

表2 常用3×3距离算子的最大绝对错误率[7]
注:a为算子上下左右的值;b为4个`对角的值。
2.2.4 结果表达与输出
模型初始化后,对每一时刻t,元胞根据状态转换规则进行绕障欧氏距离变换和数据更新,直到所有的元胞状态都稳定为止(对任意元胞,fs=0),就得到模型运行结果。将结果乘以像元大小Sc即可得到该像元大小对应的绕障欧氏距离变换结果。
假设所有元胞集合为C,则模型停止的条件可表述为:对∀c∈C,有dt+1=dt,则fs=0,模型停止。
元胞自动机的优势在于能够展示元胞演化的过程。本文应用可视化工具Processing3.0展示模型演化与距离动态计算过程。模型中可视化的内容包括海陆分布、目标位置和元胞状态,其中最核心的是元胞的展示。海陆分布作为背景,根据栅格值将海洋和陆地分别设置为蓝色与淡黄色;目标位置采用圆点表示;元胞状态的显示采用渐变颜色表示,涉及颜色的映射,通过运行一遍模型后获取最大的状态值,再进行颜色映射以获取良好的可视效果。
模型的目的除了观察计算过程,最重要的是结果分析。将元胞的最终状态值按照行列号组合形成一个二维数组,根据像元大小Sc、左上角投影坐标,行列数,输出为地理信息系统(geographical information system,GIS)软件支持的ASCII码格式文件,以便后期分析处理。
3 结果与讨论
3.1 绕障欧氏距离变换模拟结果
将目标点数据与预处理后的环境栅格输入模型,创建250 000个元胞组成的CA模型,采用表2最后一个算子,模拟绕障欧氏距离变换过程,结果如图2所示。可以看出,模型动态地展现出距离变换的计算过程。计算的元胞数量围绕目标点呈正方形向外逐渐增多,颜色也越来越深,说明元胞状态随着扩散更新。当两个目标点的扩散圈相遇时(如图2中的B位置),接缝处(T=150的B位置)过渡自然,没有出现横竖形状的突变状态。这是由于计算过的元胞依然会根据邻域情况作状态更新。当扩散至障碍区域时,会绕过陆地,元胞状态值(如图2中的A点)反映了绕障欧氏距离。在T=240时,表示模型经过240次迭代,从目标经海域能到达的区域元胞完成距离计算,共运行了23.363 s。以上结果表明,基于CA的海上距离分析模型能够动态展示计算过程,距离计算自动考虑到了绕障距离花费,说明模型可行。

图2 CA模拟过程结果Fig.2 Results of CA simulation process
3.2 模拟结果与普通欧氏距离变换结果对比
为了分析模拟结果的准确度,将CA模拟结果与普通欧氏距离变换结果对比。为避免其他因素影响,只选择1个目标点,分别对研究区作CA绕障距离变换(图3(a))与欧氏距离变换(图3(b)),再对两个结果进行差值计算(图3(c))。为直观区分,图3用等值区域法表示。可以看出,模拟结果与欧氏距离分析结果具有相似的空间分布特征,大部分区域数值差距在50 km以内,CA模拟结果比普通欧氏距离普遍偏高(图3(c)中辐条之外的区域)。但在局部区域存在较明显差异,如图3中的A、B、C3个位置,普通欧氏距离变换由于不考虑障碍导致误差偏大,而本文方法顾及到了这一点。这些区域二者差距在300 km以上,差距最大的出现在马六甲海峡(图3中的C位置)。
另外,比较结果中还存在一些低于-50 km的负值,这是由于这些位置在研究区内被障碍隔开,而无法绕障到达目标点,CA模型中未参与计算(值为-1)而欧氏距离变换结果存在值所造成的。综上,基于CA的距离分析方法在海上距离计算上存在很大的优势,合理考虑了绕陆地距离和无法到达的区域。
3.3 基于CA的绕障距离变换结果误差分析
本文中的模型如果不考虑障碍分布,运算结果便可与欧氏距离变换结果对比,分析本文方法的误差。在不考虑障碍分布情况下,普通欧氏距离变换结果即为真值。这时,设CA模拟结果为Ra,真值为Rb,则误差E可由式(4)表示
E=(Ra-Rb)/Ra
(8)
据此计算得到的模拟结果、真值和误差分布如图4所示。从图4(a)与图4(b)对比可以看出,本文模拟结果等值线呈现出正八边形的特征,这是由于邻域考虑的是8邻域所导致的。而真值是呈圆型分布,这成为了误差的主要来源。从图4(c)可看到误差的分布具有伞状特征。正八边形边的中点(即米字形表示的方向)处误差为0,其余位置误差则与其与目标连线与8个方向最小夹角有关,夹角越大则误差也越大。从误差统计结果可以看出CA距离分析方法的误差范围为0~3.96%。

图3 模拟结果与欧氏距离分析结果对比Fig.3 Comparison results of CA simulation and Euclidean distance transformation

图4 距离分析CA模型误差分析Fig.4 Error analysis of CA based distance analysis
在有障碍的情况下,绕障距离变换值为到目标最短路径的长度Lp,可以转化为多条线段的长度和。即
(9)
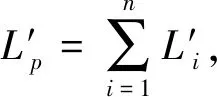
(10)
因此,本文提出的绕障欧氏距离变换的最大误差率也为3.96%。
3.4 元胞大小和转换规则对结果的影响
3.4.1 元胞大小对绕障距离变换结果的影响
本文元胞大小与地理信息系统中栅格的像元大小相对应。由研究方法描述可知,本文方法并不受元胞大小的限制,任意元胞大小都可以使用。但元胞大小对结果运算速度和计算精度有影响。
从运算速度来看,对特定的研究区域,元胞越大,则该区域元胞数量越少,运算速度越快;元胞越小,则该区域划分后的元胞数量越多,运算速度越慢。
从计算精度来看,最终的绕障欧氏距离变换结果等于元胞自动机模型模拟结果乘以元胞大小(分辨率)。因此,计算精度可由式(11)计算
ε=min(a,b)×Sc
(11)
式中,ε表示计算精度;a为距离算子上下左右位置的值;b为距离算子4角的值;Sc为元胞大小。
在式(11)中,距离算子的值相对固定,因此计算精度与元胞大小成正比。元胞越大,精度值越大,精度越低。元胞越小,精度值越小,精度越高。例如本文试验中:a=0.961 94,b=1.360 39,Sc=5 km,因此计算精度为4.809 7 km。
运算速度和计算精度相互制约,在具体应用中,像元大小的设置需在运算速度和计算精度中权衡选择。
3.4.2 转换规则对绕障距离变换结果的影响
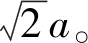
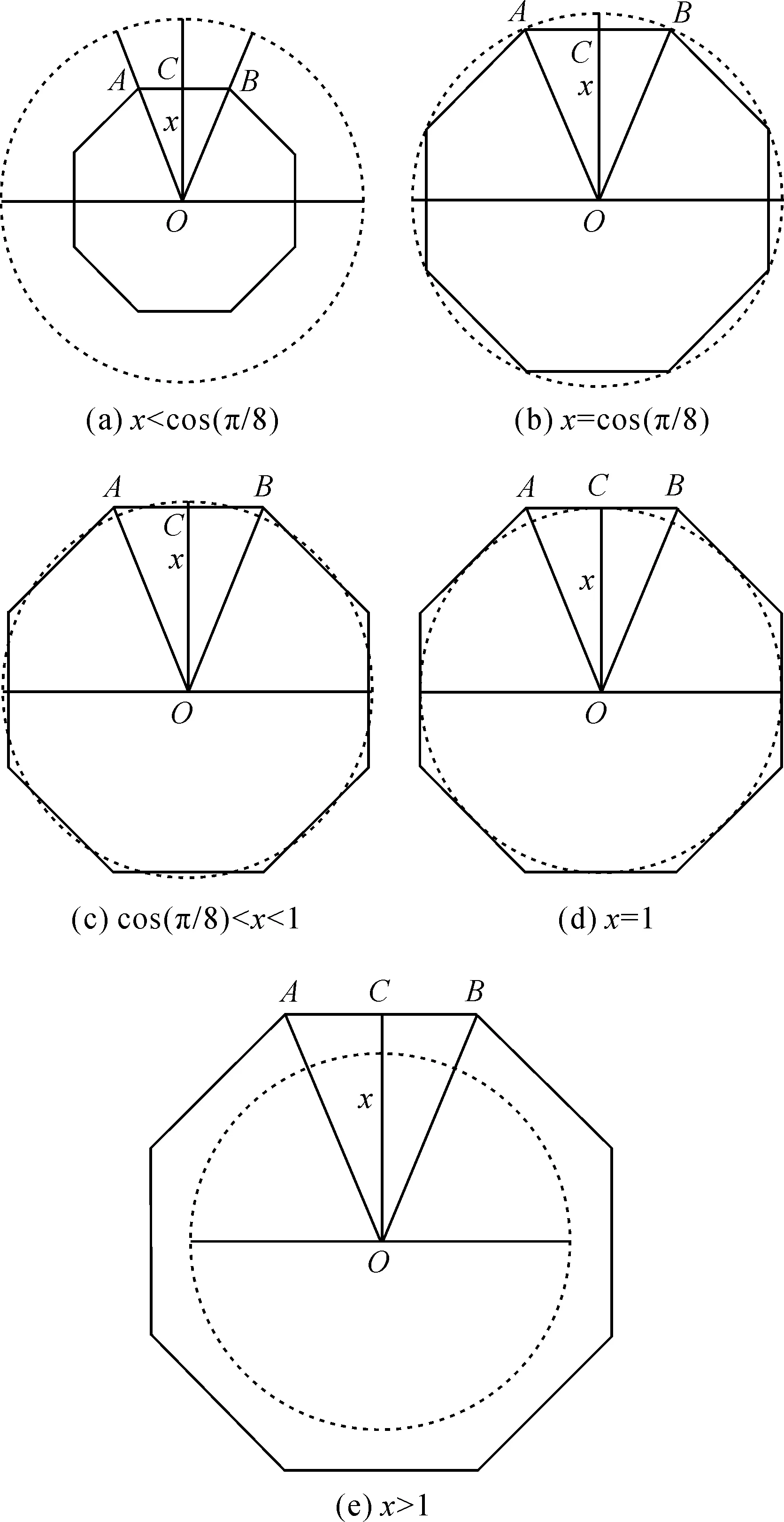
图5 距离算子对最大绝对错误率影响示意图Fig.5 The influence of distance to maximum absolute error ratio
(1) 当x (2) 当x=cos(π/8)时,圆O为八边形的外接圆,最大绝对错误率体现在O与边垂直方向。 (3) 当cos(π/8) (4) 当x=1时,圆O为八边形的内切圆,最大绝对错误率体现在O与顶点连线方向。 (5) 当x>1时,圆O在八边形的内部,最大绝对错误率体现在O与顶点连线方向。 通过几何分析得出最大绝对错误率y与x的关系如下 (12) 进一步简化为 (13) 从以上公式可看出,当0 本文以南海为例,基于海陆分布数据(障碍分布)和目标点数据,提出了一种基于CA的绕障欧氏距离变换模型,模拟后得到变换结果,并对其绕障效果和精度进行分析。本文得到以下结论:①CA为绕障距离变换提供了一种解决方案,直观动态地展示绕障欧氏距离变换的计算过程,是一种计算可视化的实现方式;②CA绕障距离变换模型在运行中能够自动更新,两目标的距离扩散接缝处过渡自然;③受格网和邻域的影响,基于CA的绕障欧氏距离变换结果为绕障至目标最短路径长度的近似值,采用Butt-Maragos优化算子,误差比例低于3.96%。计算结果可应用于航线设计、海上救助等领域。 由于误差的存在,如何通过对变换结果后续处理以改进基于CA的绕障欧氏距离变换的精度,有待进一步研究。4 结论与展望
