任意形状曲线刃边的点扩散函数估计方法

李真伟，崔国忠，郭从洲，刘 阳

1. 信息工程大学基础部，河南 郑州 450001； 2. 上海工程技术大学管理学院，上海 201620

光学系统的点扩散函数(point spread function,PSF)的精确估计是提高图像光学质量的必要前提[1]之一。通常，以h(x,y)代表点扩散函数矩阵。很多情形下，只能利用成像系统的参数或获取的图像对系统退化函数进行辨识以获取准确的h(x,y)。常利用遥感图像中的刀刃目标、线性脉冲目标及方波目标来获取准确的h(x,y)[2]。但是这些传统方法均要求严格控制靶标的形状及摆放的角度[3-4]。为了克服对靶标的依赖，很多方法，例如多通道盲反卷积[5-8]、基于联合变换的方法[9]、基于全变分正则化盲复原的方法[10]被提出并进行研究测试。这些方法虽然时间开销小，但是效果很一般。文献[11]建立了带有参数的高斯型点扩散函数模型，调整参数获得合适的h(x,y)；文献[12]提出了一种利用双刃边的方法估算运动模糊，但这些方法适用范围均较小。近年能适应更多场景的利用刃边法进行h(x,y)估计的研究逐渐展开[13-15]，主要针对倾斜直线刃边[16]以及曲线刃边的情况。

对于直线刃边，传统的刃边法只限于应用在理想刃边区域[17]。文献[18]给出了对齐拐点的方法，但是对于刃边倾角较大的情况，由于h(x,y)采样方向与刃边梯度方向不一致，样本横坐标被拉伸，会产生不可避免的误差[19]。文献[20]通过模拟离散卷积过程建立样本h(x,y)与真实h(x,y)的关系方程组，并通过最小二乘法求解真实h(x,y)。虽然该方法从离散的角度在原理上解决了倾斜直线刃边下获取真实h(x,y)的方法，但是在无法知道h(x,y)准确尺寸的情况下无法建立样本h(x,y)与真实的h(x,y)之间关系的方程组。此外，该方法对刃边边缘准确度的要求极其苛刻并且对噪声异常敏感，而采用的离散模型会产生亚像素点位误差，直接影响h(x,y)的估计精度。倾斜刃边法(投影法)[21]是一种较为成熟的方法。该方法将像元点投影到刃边垂直方向上，以获得较为准确的h(x,y)的采样数据。该方法解决了亚像素点位误差的问题，同时在投影前不需要知道h(x,y)的准确尺寸，是目前较为有效的任意倾角的直线刃边点扩散函数估计方法。

尽管最近几年提出了很多种解决弯曲刃边获取h(x,y)的方案，但是大部分方法的思路可以归结为两种：基于ISO12233[22]及其一系列改进的方法(传统刀刃法)；将像元点灰度值及点到弯曲刃边的距离组成集合后进一步处理的方法(曲线拟合法)。文献[23]直接通过对边缘扩散函数(edge spread function,ESF)曲线族微分得到的线扩散函数(line spread function,LSF)进行曲线族的对齐及样本重采样，最终得到唯一的LSF曲线。但只有在曲线每个点的切线都满足理想倾角时该方法才较为准确，否则会使横坐标拉长导致h(x,y)测量不准确。文献[22]采用二次多项式拟合弯曲刃边，将像元点灰度值以及点到弯曲刃边的距离值加入距离—灰度集合中，最后用集合中的元素拟合Fermi函数作为实际的ESF曲线。一方面，该算法使用了模拟退火算法导致迭代次数过多，时间开销大。另一方面刃边边缘很难用二次函数完美拟合。事实上，将像元点的灰度值以及点到弯曲刃边距离作为ESF样本的参考本身就值得商榷，这将在后面指出。一般的弯曲刃边图像分为左右型和上下型(图1(a)、(b))，为方便起见，将默认以左右型进行讨论，上下型的刃边以此类推。

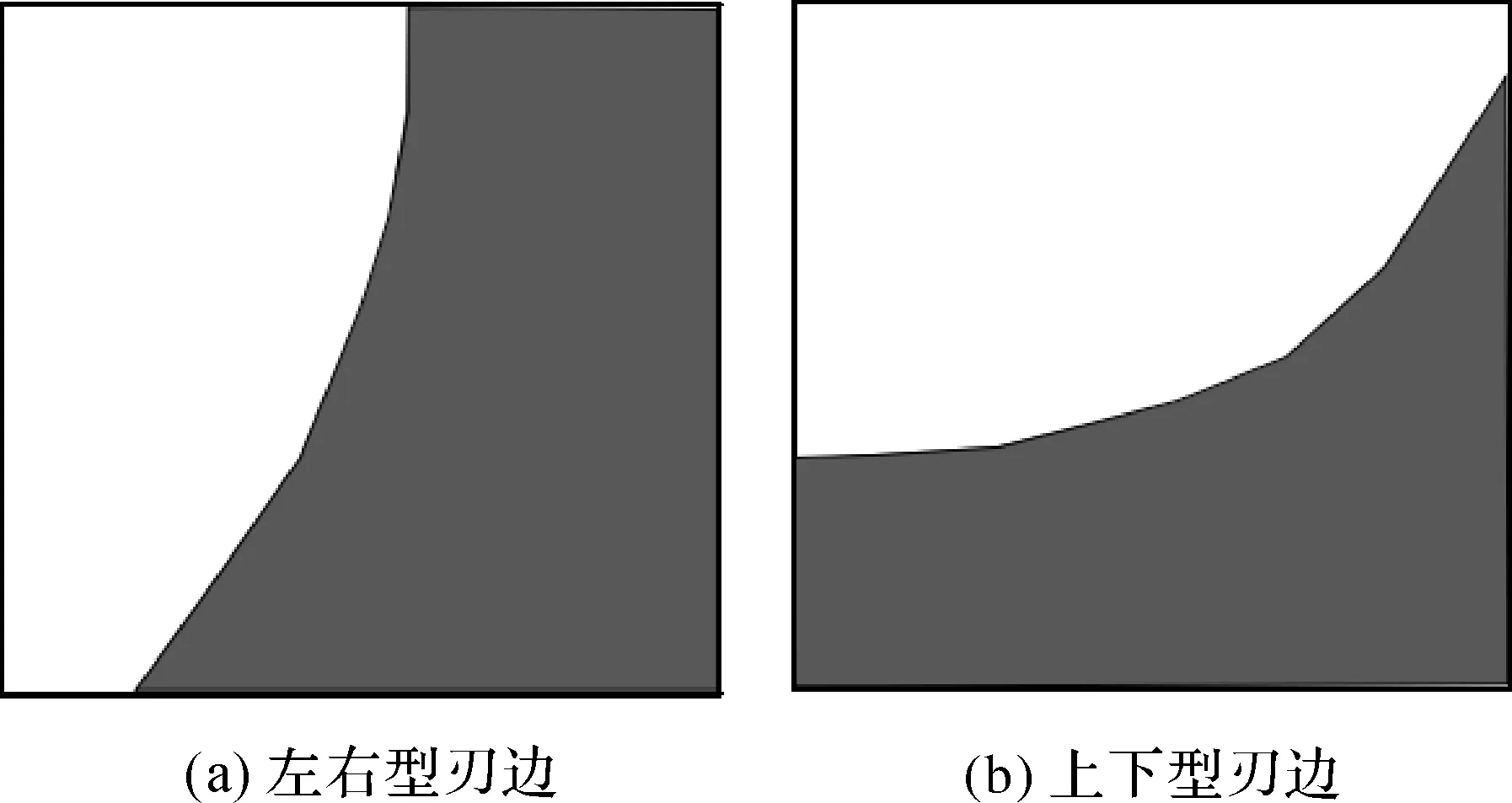
图1 刃边图的分类Fig.1 Classification of edges

为降低对靶标的要求，针对弯曲刃边处理较为困难的现状，本文提出了一种弯曲刃边的点扩散函数估计方法。对于曲率在0.001～0.01的刃边，本文算法在较强模糊下，峰值信噪比依旧能保持在35 dB以上，测得点扩散函数峰值的误差可以控制在20%以内。试验结果与现有较新文献进行了比较，提出的算法峰值信噪比平均能提高10 dB以上，且具有一定抗噪能力。在很大程度降低了对遥感图靶标的要求，可以适应各种复杂的弯曲刃边环境。

1 刃边法点扩散函数估计原理

设清晰图像为e(x,y)，退化图像为o(x,y)，遥感图像退化模型可以描述为[24-25]

o(x,y)=e(x,y)*h(x,y)+n(x,y)

(1)

式中，h(x,y)为点扩散函数矩阵；n(x,y)为加性噪声；*表示卷积运算。

一般情况下h(x,y)具有可分离性[26]

h(x,y)=hx(x)hy(y)T

(2)

式中，hx(x)是水平采样方向的h(x,y)，hy(y)为垂直采样方向上的h(x,y)。hx(x)和hy(y)被称为LSF。一般情况下，假设h(x,y)是对称的，即hx(x)和hy(y)默认相等。如果假设U(x)为垂直于刃边方向上的阶跃函数，有

g(x)=U(x)·hx(x)

(3)

式中，g(x)为该方向上的输出函数，即ESF，其与LSF的关系是

(4)

理想倾角下刃边法获取PSF使用ISO12233倾斜刃边法计算PSF[27](见图2)。基本思想是利用采样得到的灰度图计算得到ESF样本后微分得到LSF样本，也就是一维点扩散函数。但是该传统刃边方法仅仅适用于采样间隔为一像元单位的理想刃边区域。

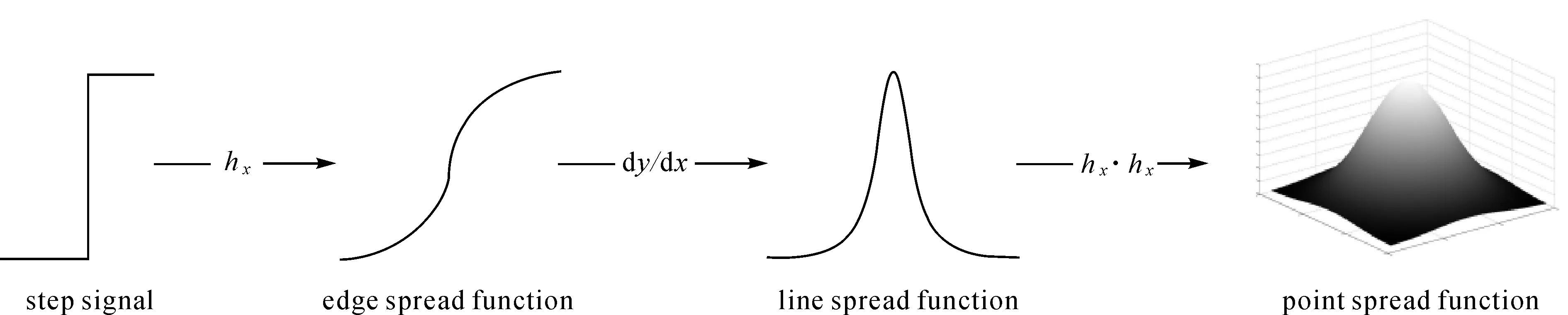
图2 刃边法Fig.2 Edge method

2 算法原理

2.1 投影法原理

本文基于投影法提出一种点扩散函数估计的弯曲刃边法。很多文章中运用投影法在倾斜直线刃边下估计h(x,y)，但是很少有文章说明投影法的理论依据。本文从倾斜直线出发分析投影法内在的物理意义。图像的退化可以表示成离散卷积

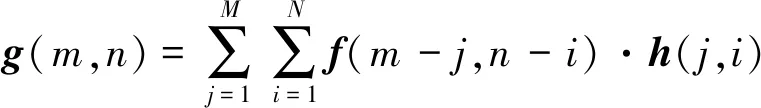
(5)

式中，g为退化的图像；f为原图像。由式(2)假设PSF分解后长度为5的LSF为hh=[u1,u2,u3,u2,u1]。45°的倾角的刃边边缘见图3(a)，图中深色的部分表示灰度值较高的部分。其经过上述PSF退化后的像元如图3(b)所示。

由于颜色区分度不高，为清楚地表示，图中的数字是将灰度值从小到大排序之后的结果，数字越大，代表灰度值越高。图中的直线是理论上的刃边边缘。其中-3位置的点的灰度值为

g(-3)=SUM(PSF·

(6)

-4位置的点的灰度值为

(7)

离散条件下有以下结论：

在离散条件下，退化后像元的灰度值等于退化前以该点为中心的h(x,y)大小的区域的灰度值与h(x,y)对应位置值点乘后的和(见图4(a))。

图3 退化前后的45°倾角刃边Fig.3 Edge of 45° before and after degeneration

在离散条件下投影法的原理可以理解为：保持像元点到刃边边缘的距离不变，退化前以该点为中心的h(x,y)大小的区域的灰度值与h(x,y)对应位置值点乘后求和的结果不变。进一步，由于h(x,y)的值以及退化前刃边边缘两端灰度值均为常数，可以理解为：保持像元点到刃边边缘的距离不变，退化前以该点为中心的h(x,y)大小的区域内灰度值的和保持不变(见图4(b))。但是在离散的情况下投影法的理论依据并不满足，直观上可以从图4(b)中观察到，保持像元点到刃边边缘的距离h不变，刃边边缘的两端面积却发生了改变。

图4 离散条件下投影法的理论依据Fig.4 The theory evidence of projection method under discrete conditions

造成这种矛盾的原因是真实的h(x,y)以方阵来描述是建立在方阵足够大的前提下的，更准确的描述是以某点为圆心向外扩散的圆，并且h(x,y)上的点的值仅与该点距离h(x,y)中心的距离有关(见图5(a))。在真实亚像素条件下，退化后亚像素像元点的灰度值g为

(8)

式中，Ω1、Ω2分别为退化前以像元点为中心的h(x,y)大小的圆所覆盖位置被刃边边缘所分割的两块区域(见图5(b))；g1、g2分别为退化前Ω1、Ω2区域所对应的灰度值；F代表归一化后h(x,y)各位置灰度值函数。

在直线刃边的情况下，由于刃边同到刃边的最短距离的直线必定垂直，所以只需要通过h(x,y)的值以及亚像素像元点到刃边的距离，就可以由式(8)计算出退化后该像元点的灰度值g。同时，无论将刃边旋转到任何角度，退化前以该点为中心的h(x,y)大小的圆内Ω1、Ω2部分的积分值不会发生改变(见图5(c))，也就是说该像元点到刃边直线的距离可以认为是理想倾角下距离刃边边缘的横坐标距离。这就是投影法进行h(x,y)样本采样的理论依据。

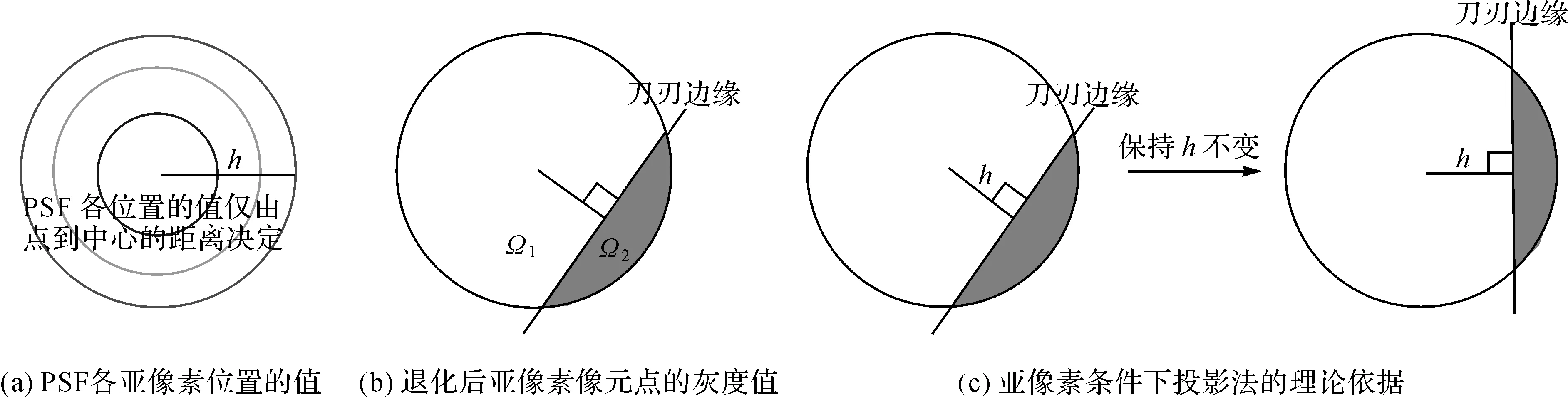
图5 真实的亚像素条件下投影法的理论依据Fig.5 The theory evidence of projection method under real sub-pixel conditions

2.2 曲线刃边投影法理论依据

在上节基础上考虑弯曲刃边时就会发现：单纯寻找每一点到曲线刃边的垂直距离作为h(x,y)样本的横坐标的参考会产生巨大的误差，因为这个距离反映的仅仅是该距离下直线刃边的情况(见图6(a))，这也验证了本文算法的问题。并且由于曲线方程难以找到合适的表达式，很难通过计算来确定这些覆盖的部分。事实上，只需要得到精确的部分h(x,y)样本，并不需要每个退化后的点都为h(x,y)样本的采样点。如果能够选出曲线刃边中较为平缓(曲率半径较大)的部分周围的点(见图6(b))，用直线刃边投影代替曲线刃边投影，在这些点处，点到刃边直线的距离就可以近似反映出该点为中心的h(x,y)尺寸的圆所覆盖的部分，进一步就可以通过插值和重采样较为精确地得到较好的ESF样本。

基于这种思想，本文提出了移动窗口投影的曲线刃边求解方法，每次选取一定的行拟合边缘曲线为直线并采用任意倾角直线刃边投影法进行h(x,y)样本的采样，然后向下移动步长个采样行，继续h(x,y)样本的采样，直到完成对所有样本行的采样(图6(c))，最后将那些明显不适合作为h(x,y)样本的采样点去除后得到最终h(x,y)样本并进行进一步的处理。

图6 曲线刃边投影法理论依据以及算法Fig.6 The theory evidence of projection method of curve edge and the schematic diagram of algorithm

3 算法步骤

利用移动窗口投影法，对左右型刃边的PSF计算的总体流程见图7。本节将详细说明流程中的关键步骤。

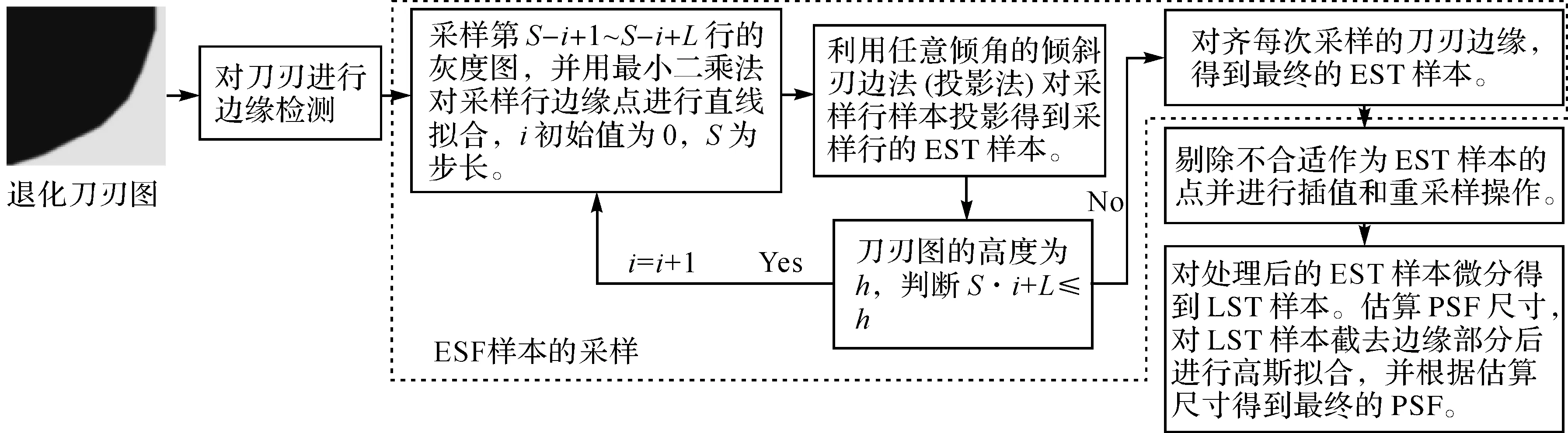
图7 算法流程Fig.7 The flow chart of algorithm

3.1 ESF样本的采样

ESF样本的采样是弯曲刃边法的核心部分。目标图像的3个超参数：移动窗口即每次采样选取的行数大小L，每次窗口移动的步长S，每次的投影中心C的选取会在试验部分给出。

单次需要处理的部分就是某一窗口中选取的行，见图6(c)。先采用最小二乘法对选定行数的边缘点的坐标进行直线拟合。其次按照任意倾角刃边投影法对选取部分进行ESF样本的采样：设拟合直线与垂直方向倾角为θ(见图6(c))，θ为小于等于45°的任意角度。采样的部分某点的坐标为(i,j)，其中i为采样点所在列数，j为所在行数，则该点投影位置的坐标P=j*cosθ±i*sinθ。(对于左下到右上的直线，符号取负，对于左上到右下的直线符号取正)。

采样完单次的ESF样本之后将窗口向下移动S个采样行继续采样，直到完成对所有样本行的采样。在每个窗口内计算投影位置坐标应默认边缘点拟合得到的直线上的点位于投影的中心位置，所以在最终得到的ESF样本中需要将投影中心对齐。为此将所有点的投影位置坐标P加上一个偏差值，设每次窗口中第一行刃边边缘对应的坐标为(io,jo)，偏差值为C-(jo*cosθ±io*sinθ)，此时对应窗口中某点(i,j)的投影位置坐标值就应当修正为P*=j*cosθ±i*sinθ+C-(jo*cosθ±io*sinθ)。将P*和对应点灰度值作为一组ESF的采样值存储。值得注意的是同一行的数据可能会按照不同的倾角采样多次，但是在刀刃边缘曲线连续且曲率不是太大的情况下，同一行得到的ESF样本投影位置坐标几乎相同。

3.2 异常与噪声ESF样本的剔除

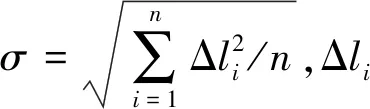
图8 容忍域Fig.8 Tolerance domain

3.3 ESF样本的插值与重采样

剔除粗差之后，一方面刃边边缘检测存在误差，另一方面ESF样本中会出现缺失值，这将影响进一步的LSF样本采样。因此对剔除粗差之后的ESF样本进行插值后重采样的操作。具体步骤如下：第1步对剔除粗差之后的样本进行插值(插值的目的是为了将剔除异常点和噪声点之后的ESF样本缺失值补上)。先按照投影位置坐标P*的大小将ESF样本进行排序，然后采用线性插值对投影位置坐标P*的取值区间中的ESF样本灰度值进行插值，移动步长为0.05像素。第2步将插值得到的点同原ESF样本一起重新按照投影位置的值P*进行排序，得到新的ESF样本。第3步对新的ESF样本进行分段拟合，移动窗口获取ESF重采样值，移动窗口的尺寸为1像素，窗口内对ESF样本进行三次多项式拟合，将窗口中心处拟合值作为重采样值，移动步长的设定比较随意，这里选择0.05像素。

3.4 LSF采样与拟合

由式(4)可知，LSF可以对ESF直接微分获得。对于离散样本，LSF可以通过ESF样本差分得到

(9)

式中，L为LSF样本；E为ESF样本。在对LSF样本进行拟合处理之前，算法先采用文献[28]的方法估算了LSF尺寸的大小。文献[28]中只考虑了4个方向，对于不是这几个方向的直线会出现偏差。提出的算法中处理的数据是投影差分后的LSF样本，因此并不会出现文献[28]中的问题。噪声会干扰轮廓值(LSF尺寸)的准确性，因此本文设定了一个阈值加以限定。为确定轮廓大小，从左端(右端)开始遍历获得的LSF样本(采样间隔为0.05个单位长度)。当某一点连同其相邻的两点都大于某个阈值的时候将其坐标记录为端点1(端点2)。阈值视噪声大小而定。由端点2坐标减去端点1坐标并向下取整得到轮廓值大小。

下面对LSF进行尾部截取以减弱LSF尾部抖动影响，为了保证LSF拟合的准确性，最终截取部分的长度应小于之前得到的轮廓值的大小。LSF的形状近似于高斯型，为了减少估计的误差，对得到的LSF样本进行一维高斯函数拟合。拟合模型可以表示为

h(x)=Aexp[-(x-u)2/2σ2]

(10)

式中，A为拟合后的峰值；u为拟合中心点的位置；x为LSF的位置；σ为拟合高斯函数的标准差。可依据最小二乘原理对上述模型进行求解。最后以u作为截取的中心截取轮廓值的大小得到最终的LSF向量。由式(2)，h(x,y)可以通过两个方向的LSF向量乘积得到，归一化之后就是最终的h(x,y)。

4 试验测试

4.1 参数的选取

试验测试需要确定3个超参数，分别是投影的中心位置常数项C，每次采样的行数L以及框架移动的步长S。投影中心的常数项C选择相对随意，仅需要保证每个样本投影后的坐标为正即可。在比较刃边算法性能的时候，常用峰值信噪比(peak signal to noise ratio,PSNR)作为算法性能的客观评价指标[29]。每次选取的行数大小L与图片或者h(x,y)的尺寸有着很大的关系。本文先以128×128的模拟图为例(见图9(b)和图9(c))，以选取的行数为自变量，以所估h(x,y)与真实值的峰值信噪比作为因变量，最终得到的结果如图9(a)所示。图中的3条曲线分别是以2作为步长h(x,y)尺寸为5×5，9×9，以及15×15的每次取样行数与峰值信噪比的关系图。图中可以看出，最优的选取行数与h(x,y)的大小无关，每次采样行数在10左右的时候峰值信噪比会比较稳定，采样行数过小或者过大都会对结果产生影响。确定每次采样的行数与h(x,y)的尺寸无关以后本文又以64×64的模拟图进行同样的试验，最优选取行数在5左右。由此最优选取行数一般为采样图片尺寸的十分之一左右。

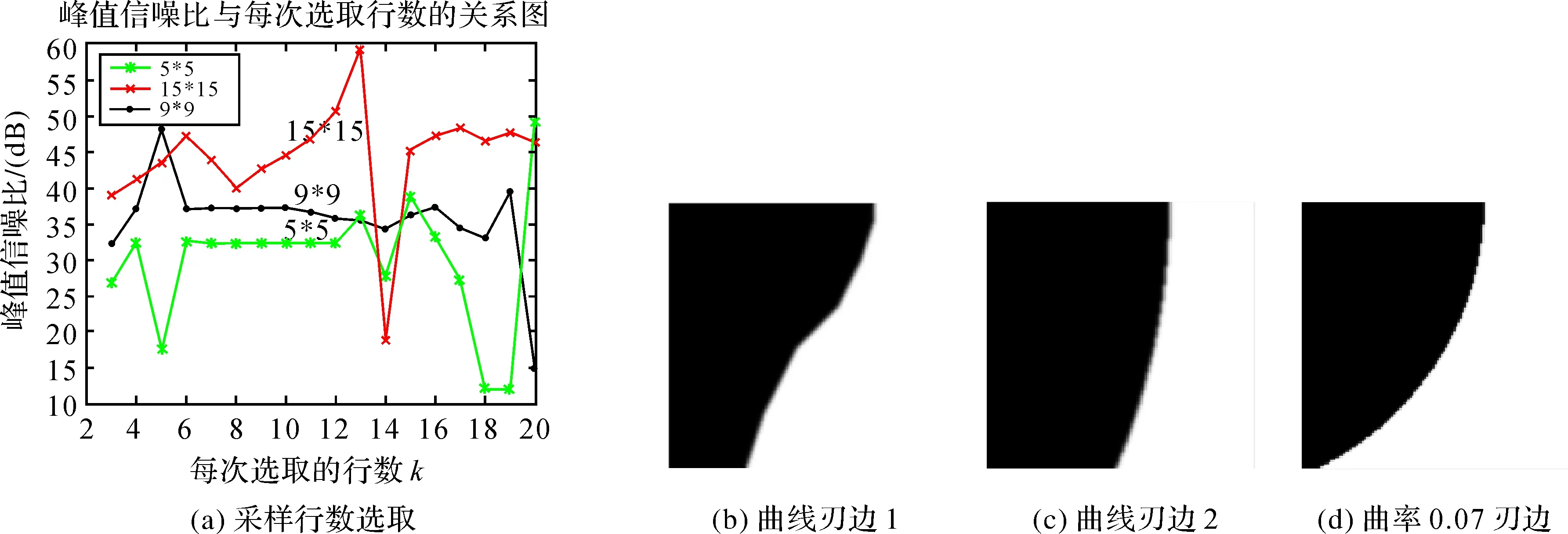
图9 参数选取及模拟图Fig.9 Parameters selection and simulation diagram

4.2 不同曲率刃边试验结果

为验证本文方法在理论上的可行性及测试算法的极限，本文针对不同曲率的曲线进行试验，利用半径为R的圆曲率为1/R的性质，可以在理论上构建任何曲率的曲线，但是一方面受到h(x,y)尺寸的限制曲率不能过大，一方面曲率过小曲线将接近直线，这里仅仅考虑曲率在0.001～0.01的情况：对不同曲率的曲线图分别进行尺寸为15×15,方差为0.5和1的高斯滤波，PSNR与曲率的关系图分别见图10的模拟结果1和2。在结果2中选取曲率为0.07的刃边，获得的LSF曲线与真实LSF曲线的比较图见图10模拟结果3，获得的LSF曲线与真实LSF曲线基本吻合。对于曲率在0.001～0.01的刃边，提出的算法在方差为0.5的较弱模糊下，PSNR保持在40 dB以上，而在方差为1的较强模糊下，PSNR依旧能保持在35 dB以上，测得PSF峰值的误差可以控制在20%以内。

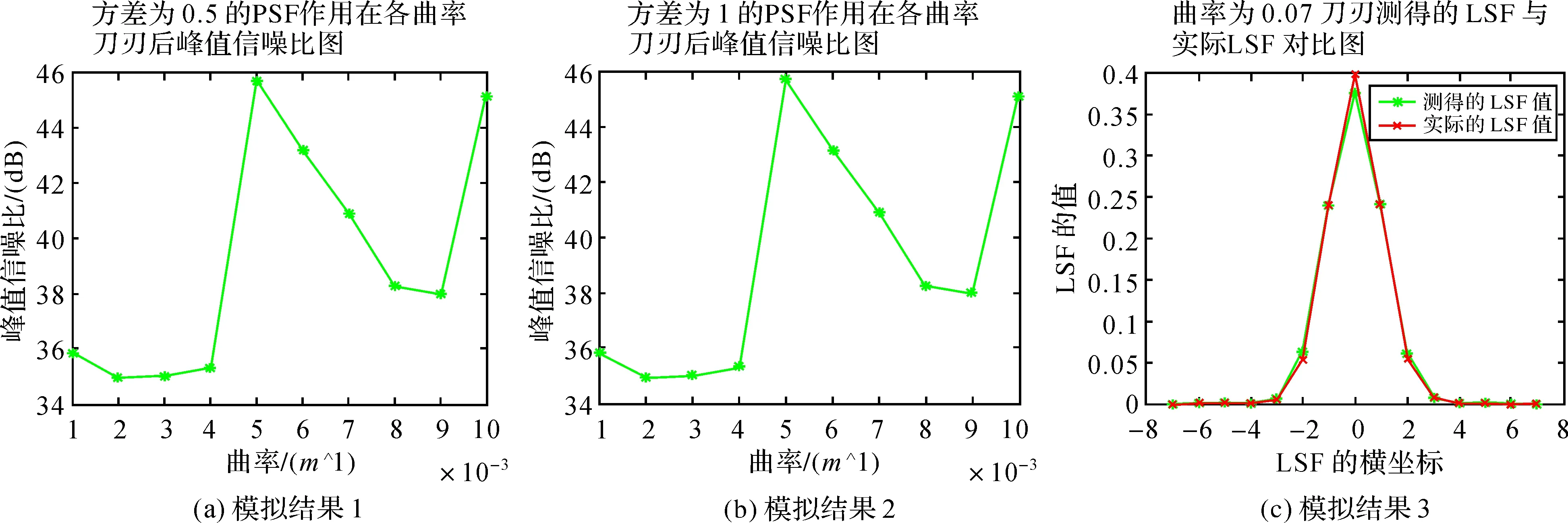
图10 模拟试验结果Fig.10 Results of simulation experiment

4.3 不同曲线刃边算法的比较

选取不同的曲线刃边以及方法进行对比试验，分别以两个角度的曲线刃边图(如图9(b)(c))对传统刃边法、二次曲线拟合法以及提出的方法测试，最终的试验结果记录在表1。对于两种曲线刃边，传统刃边法都有比较稳定的效果，但是曲线拟合法却在测量结果上出现了很大幅度的波动，一些情况下甚至会出现测量严重不准确的情况。为对比效果，对曲线刃边2进行尺寸为15×15,方差为1的高斯滤波后的结果，分别用3种方法测得的PSF进行维纳滤波。用真实h(x,y)，本文测得的h(x,y),传统刃边法测得的h(x,y)复原结果,曲线拟合法测得的h(x,y)进行维纳滤波的结果分别见图11(c)、(d)、(e)、(f)。由于测量偏差大，传统刀刃法测得h(x,y)复原结果出现了严重的振铃效应，而曲线拟合法测得的h(x,y)复原结果则和复原前模糊图几乎相同。提出的算法在各种情况下都要远远优于其他两种算法，PSNR平均可以在最优效果的基础上提高10 dB左右。

图11 不同方法测得的PSF维纳滤波复原后效果Fig.11 Images after restoration by Wiener filtering using PSF measured by different methods

4.4 算法的抗噪性研究

为测试噪声对于算法的影响，分别对曲线刃边1用尺寸15×15，方差为1的PSF高斯滤波后的模拟图中加入高斯噪声以及随机噪声，来测试算法的抗噪能力，结果分别见图12(a)、(b)。经测试，对于随机噪声，虽然测量精度有所下降，但是仍能较准确获得h(x,y)估计值。算法对于高斯噪声较为敏感，对于标准差在10以上的高斯噪声无法获得预期的效果。

4.5 遥感图复原效果

对于真实场景，应当选取边界为阶跃变化且未受到强噪声污染的弯曲刃边作为靶标图，同时应当保证刃边曲率在0.1以下。本节中选取某卫星遥感图一部分进行测试，对场景进行大小为9×9，方差为1的高斯滤波后，截取中间64×64大小的作为靶标，采用本文方法进行弯曲刃边法测试如图13(a)，最终测得的LSF曲线与真实LSF曲线对比图见图13(b)。图13(c)和图13(d)分别是退化图采用算法估计的h(x,y)进行维纳滤波前后截取的同一部分的结果。可以看到，图像所能获得的刃边区域边缘经常会有不连续的点，在这种情况下，算法仍可以较好地估计出真实的h(x,y)，并且获得不错的复原效果。

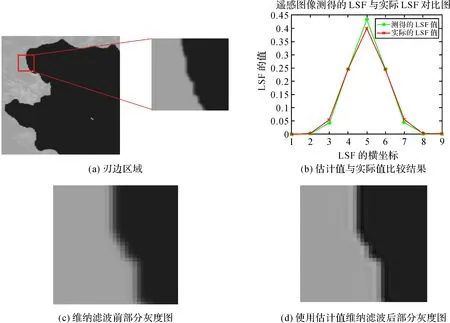
图13 遥感图像测试Fig.13 Test of remote sensing images

5 结 论

针对大量靶标受到限制条件下的遥感图像估计PSF的问题，本文提出的方法可以利用任意形状的刃边进行PSF的估计，从理论上分析了现有算法的不足以及提出方法的可行性。对于曲率在0.001～0.01的刃边，本文算法在较强模糊下，PSNR依旧能保持在35 dB以上，测得PSF峰值的误差可以控制在20%以内。相比传统刃边法和曲线拟合法，本文方法测量结果的PSNR平均可以在最优效果的基础上提高10 dB左右，对于实际遥感图有不错的效果。算法对随机噪声有一定抗性，对于高斯噪声较为敏感，只适用于标准差在10以下的场景，有待在未来的工作中改进。