Tsallis最大熵原理及其逆问题*
2019-04-11吴贤东汪加梅李婉晴
吴贤东, 汪加梅, 李婉晴
(安徽工业大学 数理科学与工程学院,安徽 马鞍山 243032)
0 引 言
1948 年,为解决信息的量化度量问题,香农提出了“信息熵” 的概念,也称为香农熵[1]。 一条信息的信息量大小和它的不确定性有直接的关系,因而香农熵也是信息不确定性的一种度量。对于一个离散型随机变量X取值{xi}的概率为P(X=xi)=pi,i=1,2,…,n,其香农熵定义为
1988年,巴西物理学家C. Tsallis提出了Tsallis熵[2]:
Tsallis熵推广了标准的统计力,Tsallis 熵和Shannon熵有如下联系:
Tsallis熵在不规则且不完全混沌中有重要应用。由于该熵不具有次可加性,因而Tsallis熵是非广延的,随之Tsallis非广延统计学也被大批学者研究[3-4]。
Tsallis最大熵原理是在Jaynes最大熵原理[5]的基础上发展而来的一种可以有效求解随机变量概率分布的方法。 它就是根据已经给出的约束条件求解出使Tsallis熵达到最大值的概率分布,例如正态分布可以利用数学期望和方差的条件,根据Tsallis熵最大自然地推出。 在刘成仕[6-7]发表的几篇有关非对称熵以及最大非对称熵原理中,提出了一种新的概念——非对称熵,它概括了玻尔兹曼熵和香农熵的概念, 证明了最大非对称熵原理,从最大非对称熵原理推导出一些重要的分布规律。 基于Tsallis最大熵原理以及贝叶斯原理[8-9],还可以研究统计学的问题。 为了解决最大熵方法的逆问题,王海虹等[10-11]提出贝叶斯参数估计的最大熵方法的逆问题,并且以泊松分布和指数分布为例给出证明,通过求解相应的微分方程和变分方程,得到所需要的约束条件。 类似地,Tsallis最大熵的逆问题就是先给出一些具体的概率分布,然后再根据Tsallis最大熵方法求解出使Tsallis熵达到最大值的约束条件。
本文主要分为5个部分,第一部分为Tsallis最大熵原理的问题来源及背景简介;第二部分主要研究了离散形式和连续形式的Tsallis最大熵原理; 第三部分研究了在约束条件下的最大熵原理;第四部分研究了Tsallis最大熵原理的逆问题, 即给定一个具体的概率分布或密度函数,获得使这个概率分布或密度函数达到Tsallis最大熵的约束条件,主要分别以二项分布和正态分布为例研究了离散情形和连续情形下的Tsallis熵原理的逆问题;第五部分为总结部分。
1 Tsallis最大熵原理
首先给出并证明离散形式的Tsallis最大熵原理.
为方便,采取如下记号:
显然,expr(lnrx)=lnr(exprx)=x.
由Tsallis熵的定义知,离散情形下的Tsallis熵可以写成如下形式:



将G对Pi求偏导,并令其为0,得到方程组:
i=1,2,…,n


下面给出并证明连续形式的Tsallis最大熵原理。

证明运用拉格朗日乘子法构造一个辅助泛函:
存在

2 约束条件下的Tsallis最大熵原理
下面研究在约束条件下的Tsallis最大熵原理. 首先,研究在约束条件下对于概率分布的Tsallis最大熵原理。
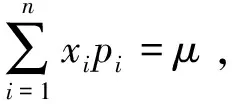
其中λ1和λ2满足两个约束条件:

证明运用拉格朗日乘子法构造一个辅助函数:
可以推出:


其中λ0和λi(1≤i≤m)满足m+1个约束条件:
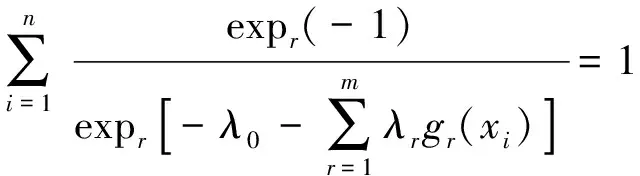
证明构造辅助函数:

即最大熵分布为
其中λ0,λ1,…,λm是拉格朗日乘子。
下面分别研究在约束条件下对于密度函数的Tsallis最大熵原理。

其中λ1和λ2满足两个约束条件:
证明运用拉格朗日乘子法构造一个辅助泛函:
由δF=0,可以推出:

其中λ0和λi(1≤i≤m)满足m+1个约束条件:

r=1,2,…,m
证明构造辅助函数:

即最大熵分布为
其中λ0,λ1,…,λm是拉格朗日乘子。
3 Tsallis最大熵原理的逆问题
下面研究离散情形下Tsallis熵原理的逆问题(以二项分布为例),即假定某约束条件下使二项分布的Tsallis熵达到最大值,反求约束条件。
若随机变量满足二项分布,则分布函数为
其中,i=1,2,…,n,0 证明应用拉格朗日乘子法求解,首先构造一个辅助函数: 由此可以得到: 将指定的二项分布代入,就可以得到: 可以进一步假设: (1) 将式(1)对i求和,则得到所要求的约束条件: 这个结果包含一个数学期望,即 因此,约束条件可以写成: 其中离散型随机变量X的取值为1,2,…,n。 下面研究连续情况下Tsallis最大熵原理的逆问题(以正态分布为例)。 其中,-∞ 证明应用拉格朗日乘子法求解,首先构造一个辅助函数: 由此可以得到: 将指定的正态分布的密度函数代入,就可以得到: (2) 将式(2)对x进行积分就可以得到要求的约束条件,即 这个结果有一个数学期望,即 因此,约束条件可以写成: 贝叶斯的均匀假设并非总是合理的,因此寻求新的确定先验分布的方法有重要意义。 利用Tsallis最大熵原理是一个有价值的方向,而其逆问题也同样有趣。用了二项分布和正态分布这两个代表性的实例给出处理这类问题的方式,其他分布形式也可以用此方式做出。 其约束条件往往以随机变量函数的数学期望形式出现,这符合最大熵原理的使用经验。Tsallis最大熵原理的逆问题的解一般不是唯一的。

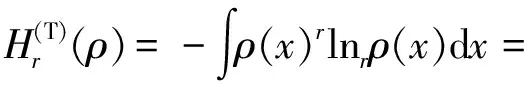


4 总 结
