离散型Z-number效用的计算及其应用*
2019-04-11吴敏超毛军军姚登宝
吴敏超, 毛军军,b, 姚登宝
(安徽大学 a.数学科学学院;b.计算机智能与信号处理教育部重点实验室;c.经济学院, 合肥 230601)
0 引 言
Zadeh于1965年提出的模糊集是对清晰集的推广,以此来描述模糊现象。2011年,为了处理不确定信息,以支持更有效、更可靠的决策,Zadeh在模糊集的基础上再次做了一个推广,提出了Z-number[1]的概念。Z-number是由一个有序的模糊数对(A,B)来表示的,其中元素A是不确定变量X的一个实值函数,是对X在值上的限制,而元素B是对A在概率测度上的一个可靠性的度量。比如说在实际生活中要度量一件商品的价格时,给出的评价是价格中等,而该评价的可靠性为可能是正确的,因此一个Z-number就可以写为Z=(中等,可能),其中的不确定变量为商品价格。
Z-number的提出,使得人们在处理不确定信息方面的能力显著增加,同时也使得决策更加高效可靠,因此,Z-number受到了许多专家学者在相关领域的广泛关注和研究,比如基础模糊理论、模糊决策、模式识别、金融风险、生物医药等。
Aliev等[2-3]分别就离散型Z-number和连续型Z-number进行了加减乘除等相关算子的研究;Pirmuh-ammadi等[4]介绍了Z-number的各种参数形式,并定义了Z-number的派生过程:Z-process;Kang等[5]提出了Z-number的一个效用函数并介绍了其在决策中的应用;Peng和Wang[6]提出了犹豫不确定语言Z-number(HULZNs),并介绍了其在多目标群决策问题中的应用;Wu等[7]在Z-number的基础上建立了一个新的医学诊断模型;Rahib等[8]使用Z-number模糊系统来估计食物安全风险水平;Kang[9]结合了文献[5]中提出的效用函数和博弈论建立了一个稳定策略分析模型。
本文首先介绍了模糊集以及Z-number的一些相关定义,随后,基于文献[5]介绍了两种离散型Z-number转化为连续型Z-number的方向并计算其相应的效用。在实际生活中,多属性决策问题中的权重信息通常是未知的,本文将结合离散型Z-number的效用和基于信息熵的多属性决策方法,确定多属性决策问题中的权重,从而给决策者提供相应的决策依据。
1 基础知识
这一板块将介绍一部分相关的基本概念。
定义1[10](模糊数) 一个模糊数A,在论域X上的定义如下:
A={[x,μA(x)]|x∈X}
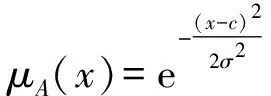
时,即称为三角模糊数。
定义2[2](离散模糊数) 对于定义在实数域上的一个模糊数A,其隶属函数μA(x):R→[0,1],称A是一个离散模糊数,如果A的支撑集是有限的,即对于任意的r1,r2,…,rn∈R,且r1
(1)∀i∈[s,t],μA(i)=1;
(2)∀i,j∈[1,s],i (3)∀i,j∈[t,n],i 定义3[10]A是定义在论域X上的一个模糊数,λ∈[0,1],记Aλ={x∈X|A(x)≥λ},称Aλ为A的λ-截集,或称为A的λ-水平集。 定义4[5]Z-number是由有序的一对模糊数组成的,记为Z=(A,B)。其中,模糊数A是不确定变量X的实值函数,是对X在值上的约束;模糊数B是对A的可靠性的测度。 定义5[2]一个离散Z-number是一个有序模糊数组Z=(A,B),其中A是一个离散模糊数,其隶属函数μA:{x1,x2,…,xn}→[0,1],x1,x2,…,xn⊂R,B也是一个离散模糊数,其隶属函数,μB:{b1,b2,…,bn→[0,1],b1,b2,…,bn⊂R。 定义6[5](Z-number效用)对于任意一个Z-number,称 (1) 为Z-number的效用,其中[A-(α),A+(α)]为模糊数A的α-截集(α∈[0,1]),[B-(β),B+(β)]为模糊数B的β-截集(β∈[0,1])。 定义6介绍的Z-number效用实际上只是针对连续型Z-number,即模糊数A和B均为连续型模糊数情形下的Z-number,而对于离散型Z-number的场合,Z-number的效用就不适用了,因此,定义6中的Z-number效用实际上是有一定局限性的。下面,将介绍两种将离散型Z-number转化为连续型Z-number的方向,从而计算离散型Z-number的效用。 由离散模糊数的定义不难发现,其隶属度随着变量的分布趋势是先增后减的,其散点图要么呈钟型分布(图1),要么呈近线性分布(图2),或者是上述两种分布的混合型,即左半边散点图呈钟形分布,右半边散点图呈线性分布;或左半边散点图呈线性分布,右半边散点图呈钟形分布。 图1 隶属度散点图(a)Fig.1 Scatter of membership value (a) 图2 隶属度散点图(b)Fig.2 Scatter of membership value (b) 2.1.1 基于3σ原则转化离散模糊数 若散点图呈钟型分布(图1),当n→∞时,A的隶属函数图像近似于正态(高斯)分布函数图像。基于此种情形,可以利用3σ原则,将一般的离散模糊数转化为高斯模糊数。 步骤2 取c-3σ1=r1,c+3σ2=rn,即有 (2) 步骤3 取σ=max{σ1,σ2},这样就能保证离散模糊数的所有点都落在[c-3σ,c+3σ]区间中,此时离散模糊数A即转化为高斯模糊数A=(c,σ)。 2.1.2 基于线性函数转化离散模糊数 若散点图呈近线型分布(图2),当n→∞时,A的隶属函数图像近似于一个梯形函数图像。基于此种情形,可以利用线性函数,将一般的离散模糊数转化为三角模糊数(不转化成梯形模糊数主要是因为梯形模糊数代入式(1)的计算太过复杂)。 (3) 步骤4 取d=max{|a2-a1′|,|a2-a3′|},然后令 (4) 此时离散模糊数A即转化为三角模糊数A=(a1,a2,a3)。 综合2.1中的两种转化方法,即可将任意一个离散型Z-number转化成连续型Z-number,其中模糊数A和B可以是高斯模糊数和对称三角模糊数的两两组合。 文献[5]中介绍了模糊数A和B均为高斯型模糊数和对称三角模糊数情形时Z-number的效用的表达式。当A=(c1,σ1),B=(c2,σ2)时,Z-number效用为 (5) 当A=(a1,a2,a3),B=(b1,b2,b3)时,Z-number效用为 (6) 其中,2a2=a1+a3,2b2=b1+b3。 事实上,由Z-number效用的定义式的结构特点,以及式(5)(6)的结构特点,不难发现: 当A=(c1,σ1),B=(b1,b2,b3)时,Z-number效用为 (7) 或当A=(a1,a2,a3),B=(c2,σ2)时,Z-number效用为 (8) 从而式(5)(6)(7)和(8)即为离散型Z-number在各种情形下的效用计算公式。 在任何时候任何市场环境下,企业信用都至关重要,只有有良好信用的企业,才会有长远的发展,信用良好的企业会在许多方面受益;反之,信用不良也要承担应有的后果。因此如何综合评价一个企业的信用是一个至关重要的问题。现有一企业准备在4个目标企业{a1,a2,a3,a4}中挑选一个信用最好的企业合作。该企业利用语言评价S=(s0,s1,…,s6)={很差,差,较差,一般,较好,好,很好}(表1),以及T=(t0,t1,…,t6)={很不可靠,不可靠,较不可靠,一般,较可靠,可靠,很可靠}(表2)来对4个目标企业的6个属性:政府监管信息、银行信贷信息、行业评价信息、媒体评价信息、企业运营信息、市场反馈信息{c1,c2,c3,c4,c5,c6}做出评价(表3)。下面将结合基于信息熵的多属性决策方法计算上述6个属性的权重信息。 表 1 S中的语言评价与对应的离散模糊数Table 1 Linguistic terms in S and corresponding discrete fuzzy numbers 表 2 T中的语言评价与对应的离散模糊数Table 2 Linguistic terms in T and corresponding discrete fuzzy numbers 表3 企业属性信息Z-number矩阵Table 3 Z-number matrix of company attribute 步骤1 将表1,表2中的数据按2.1中的两种方法分别转化成对称三角模糊数和高斯模糊数,如表4; 表4 T和S中的语言评价对应的连续型模糊数Table 4 Linguistic terms in Tand S and corresponding continuous fuzzy numbers 步骤2 根据表4中对应的模糊数,由式(8)计算出表3中离散型Z-number的效用(表5); 表5 企业属性信息Z-number效用矩阵Table 5 Z-number utility matrix of company attribute 步骤3 依次规范化、归一化表5,得到矩阵: 步骤4 计算属性ci输出的信息熵: i∈{1,2,3,4},j∈{1,2,…,6} (9) 由式(9)可得: E1=0.981 2,E2=0.976 7,E3=0.983 0 步骤5 计算属性权重向量w={w1,w2,…,wm},其中, (10) 于是可得 w=(0.161 7,0.200 9,0.146 2,0.323 5,0.062 2,0.105 5) 步骤6 计算企业ai的综合属性值zi(w)(i=1,2,3,4),其中, (10) 由式(10)可得: z1(w)=0.034 5,z2(w)=0.030 2 步骤7 利用zi(w)(i=1,2,3,4)对目标企业进行排序: a1>a4>a2>a3 故最优目标企业为a1。 本文基于3σ原则和线性函数,通过两种不同情况将离散模糊数分别转化成连续型高斯模糊数和三角模糊数;继而结合Z-number效用函数给出了离散型Z-number的效用计算方法,这在一定程度上丰富了Z-number效用函数的应用范围;然后结合离散Z-number效用和基于信息熵的多属性决策方法,在一个选择企业伙伴的多属性选择问题中,综合考虑各目标各属性的信息,并通过成熟的理论方法计算出各种属性的权重信息,给出目标企业的最优排序,从而为决策者提供可靠、准确的决策依据。
2 离散型Z-number的转化方法及效用
2.1 两种离散模糊数转化方法




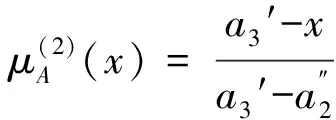

2.2 离散型Z-number的效用
3 离散Z-number效用在决策中的应用

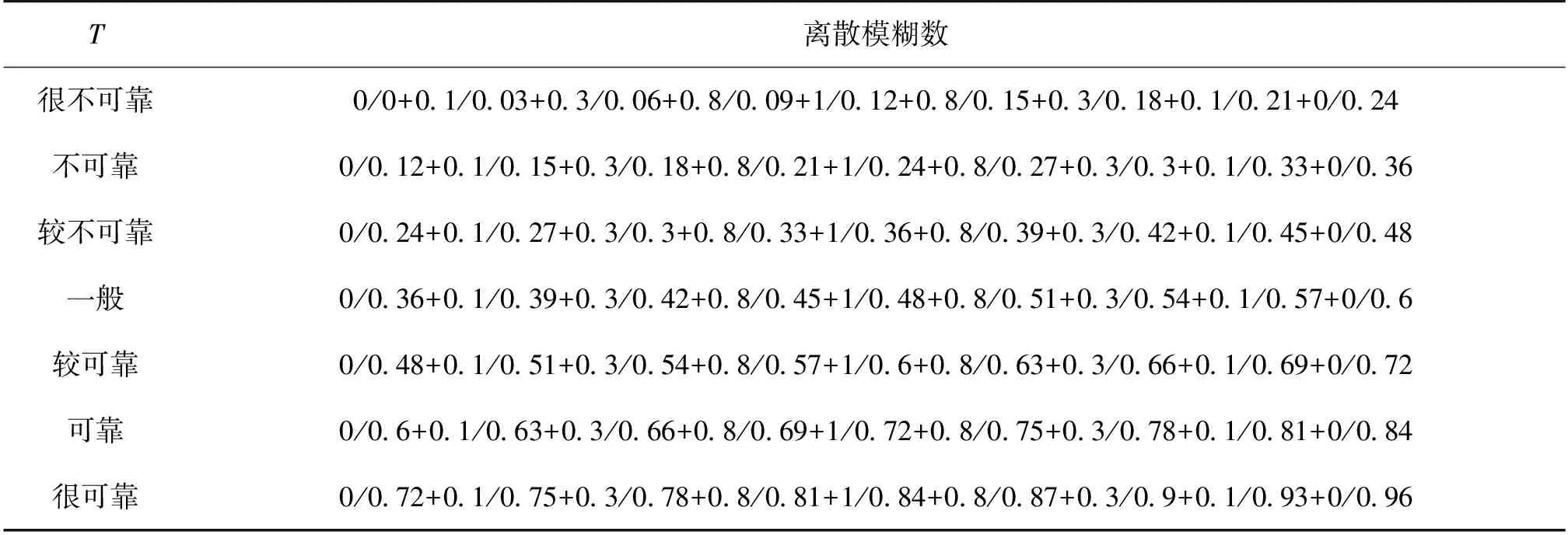





E4=0.962 5,E5=0.992 8,E6=0.987 8
z3(w)=0.024 1,z4(w)=0.034 24 结 论
