“对应方法”在小学数学教学中的应用

邹仁山

对应思想作为基本的数学思想，在小学数学教学中有着广泛的应用。如果能正确把握对应思想并以之指导教学，不但能有效帮助学生掌握一定的数学方法，还能帮助教师突破教学的重点难点，培养学生学习数学的兴趣。因此，从对应的角度来考量数学中的数与形、量与数、数与数、条件与条件、条件与问题之间的关系，是解答数学问题的基本方法和常用技巧。那么，该如何指导学生用“对应方法”来解答应用题？

一、依据对应数量的变化求解

应用对应方法来解答应用题，一般是将题中提供的相关条件，在数量上作比较，分析形成差别的原因。

例：新华书店运进文艺书1400册，运进的科技书是文艺书的3倍，运进的连环画是文艺书的2倍，书店共运进图书多少册？

对这道题的解答，可引导学生将条件进行比较，找出对应的数量：

通过寻找“对应”，学生很快列出综合算式：1400×（1+2+3）。

又如：有一塊茄子地，农民准备采摘。第一天采摘了全部的3/8，装了3筐还余12千克;第二天把剩余的全部采摘完，正好装了6筐。问这块地共收了多少千克茄子？

分析：要求全部的茄子有多少千克，只要求出12千克对应全部的几分之几就行了。已知12千克和3筐对应全部的3/8，所以只要求出3筐对应全部的几分之几就行了。已知6筐对应全部的（1-3/8），所以3筐对应全部的几分之几就清楚了。

此题有多种解法，只要认真读题，找一找其他的对应关系进行解题，就可以找出12千克所对应的筐数，然后再找出每筐所对应的分率。

二、依据相当量与绝对量的对应关系求解

在分数、倍数应用题中，需要依据已知数量（绝对量）和它所对应的分数或者倍数（相当量）来求解。在一道分数应用题中，每一个分率，都代表一个具体的量，“量率对应”是通过题中具体数量与抽象分率之间的对应关系来分析问题和解决问题。

例：某班一次数学测试，得优的与全班人数的比是1∶6，得良的占全班人数的1/4，得良的比得优的多4人，这个班的学生有多少人？

在教学时可引导学生先找出与4人对应的分率（1/4-1/6），学生便会很快地找到了解题的途径：4÷（1/4-1/6）。

当然，用对应法解应用题是指利用题目中给定的量所对应的数量关系去求解未知量，这样的问题经常出现在生活中，关键是找出对应关系。

例：某学校新收一批住校生，学校启用15间宿舍还有34人没住处，启用21间宿舍后学生不但全都住进去了，有一间宿舍还可以再住进去2人，这批学生共有多少人？

分析：启用15间宿舍——还有34人没住。

启用21间宿舍——还可以住2人。

解题的关键是要找出题目中的数量关系式，通过解题拓展学生的应用能力。

三、依据问题与条件的对应求解

应用对应方法解题，可以从问题出发，寻找与之相关的条件，从而沟通题中已知量与未知量的关系，求出正确的答案。

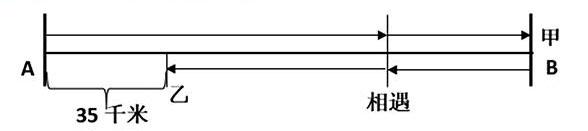
例：甲、乙两车分别从A、B两地同时相向而行，经2小时相遇后又继续前进，甲车又用1.5小时到达B法地。这时乙车距A地还有35千米。问甲车每小时行多少千米？

教学这道题时，应引导学生画出线段示意图帮助寻找对应关系。

当然，应用对应方法解题，还应遵循如下几个方面的问题：要确定找谁的对应关系，如果从已知条件不能确定寻找对象，要画出线段示意图来解决;要依据寻找到的对应关系列出综合解答算式，并作出解答;如果关系复杂，也可以列出对应表，使关系更加明朗化。总之，数学即生活，只要引导学生充分应用“对应”方法解题，让学生切实地感受数学的价值，就一定能够收到良好的效果，使学生敢解应用题，想解应用题，善解应用题，全面提升数学素养。