改进的小波阈值函数在冲击加速度信号处理中的应用

张 颖,李广武,杨建宏,郭小帆

(西安航天动力测控技术研究所,西安 710025)

加速度传感器广泛地应用于振动、冲击等非线性非平稳信号的测量中,应用涉及航空航天等多重领域。通过对加速度信号的采集分析,获取有效的物理信息[1]。由于恶劣的试验环境,航天试验中采集到的冲击信号中往往含有各种干扰噪声以及零漂现象[2-3]。

小波变换作为信号去噪的常用技术,具有低熵性、多分辨率、去相关性等特点[4]。运用小波变换去噪分为三类[5]。小波阈值去噪方法可以有效的提取冲击加速度信号的有用信息[6]。

现小波阈值去噪方法中常用的阈值函数有硬阈值函数和软阈值函数,两种函数因为计算量小,实现简单得到了广泛的使用,但是两种方法存在一些不足[7],硬阈值函数不具有连续性,软阈值函数连续但是去噪后的信号与原始数据存在固定偏差。为解决以上两种阈值函数去噪结果中问题,一些学者提出了改进的阈值方案[5,8-10],各种方案中的阈值函数在连续性与去偏差方面均有所改进,但是均为固定的两段分段函数,同时,阈值选取多采用选定固定值的方案,对于爆炸冲击这类高冲击型数据而言,可能会造成有用信息的丢失。李红延[11]等提出的阈值函数较适用于振动类型数据,但是依旧存在上述问题,同时引入了双变量,增加了不可控因素的干扰。

针对以上方法存在的不足以及冲击加速度信号的特点,本文提出了一种新的三段阈值函数,使其可以解决连续性差和存在固定偏差的问题;并设置分层阈值以保留更多有效信息。在速度检验的基础上,增加相关性检验,以直观的数据形式,验证方案的可行性。通过MATLAB仿真验证阈值函数的有效性,并对实测的加速度信号进行去噪处理,结果显示本文方法具有良好的应用效果。

1 小波阈值去噪

1.1 原理

假设有如下观测信号:

f(k)=s(k)+n(k)

(1)

式中:f(k)为含噪信号,s(k)为原始信号,n(k)为噪声。由于小波变换是线性变换,所以对带噪信号fk做离散小波变换后,得到的小波系数Wj,k仍由两部分组成,一部分是真实信号s(k)对应的小波系数,记为Uj,k,另一部分是噪声信号n(k)对应的小波系数,记为Vj,k。

Donoho[12]提出找到一个合适的λ值作为阈值,当Wj,k<λ时,Wj,k主要是有噪声引起的;当Wj,k>λ时,Wj,k主要是有信号引起的。因此,采用阈值去噪可以把信号系数保留,使大部分噪声系数减小为0。

基于小波变换的阈值去噪方法的步骤简述如下:①选择合适的小波,对所给的信号进行小波变换得到小波系数Wj,k。②计算阈值λ,并选用合理的阈值函数对小波系数Wj,k修正,得到信号的小波系数Wn。③将得到的小波系数Wn进行重构,得到去噪后的信号。

1.2 阈值选取

目前主要有以下4种阈值选取方案[13]:

①固定阈值

设噪声信号f(k)经小波分解得到N个小波系数,噪声信号均方差为σ(以下均相同),则固定阈值为:

(2)

②Stein无偏似然估计阈值

采用基于Stein无偏似然估计原理的自适应阈值。设一个风险矢量R,其元素为:

以R中最小值ra作为风险值,由ra的下标求出对应的pa,则阈值为:

(3)

③混合型阈值

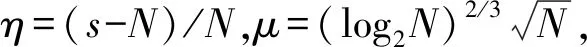
(4)

④最大最小阈值

最大最小准则阈值法采用的也是一种固定阈值,产生一个最小均方差误差极值,则阈值为:

(5)

实际应用中,阈值通常为固定阈值:

(6)

式中:σ2为噪声方差,N为采样长度。通常我们不能得到准确的噪声方差,所以噪声方差按照下式计算:

(7)

式中:MAD表示平均绝对偏差,估计噪声方差用的是第1层分解得到的高频系数cD1,因为它是最精细的分解系数,且主要为噪声系数。

由上式可知,一旦信号给定,阈值便是一个固定值,但是随着分解层数的增加,噪声的小波系数逐渐减小,借鉴文[14]中提到的阈值方案[14],本文采用改进的变阈值方法:

(8)

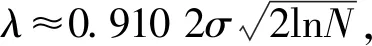
1.3 阈值函数

在对高于阈值的小波系数进行处理时,可以采用硬阈值和软阈值两种方案,两种方法的阈值函数分别如下:

硬阈值函数:

(9)

软阈值函数:

(10)

硬阈值函数和软阈值函数因为计算量小,实现简单得到了广泛的使用,也取得了较好的效果。但是两种方法存在明显的不足,硬阈值去噪处理的小波系数Wjk在λ处不连续,在重构时可能出现明显的震荡现象,而软阈值去噪处理的小波系数,因为与真实小波系数存在恒定偏差,导致重构信号精度下降。

小波去噪过程中各个尺度的消噪阈值按照折线的方式递减,根据李氏指数(Lipschitz Exponents)的理论可知对数变换域的均一李氏指数条件表示为:

log[W2jf(a,b)]≤log2K+jα

(11)

本文提出一种新的阈值方案,其阈值函数为:

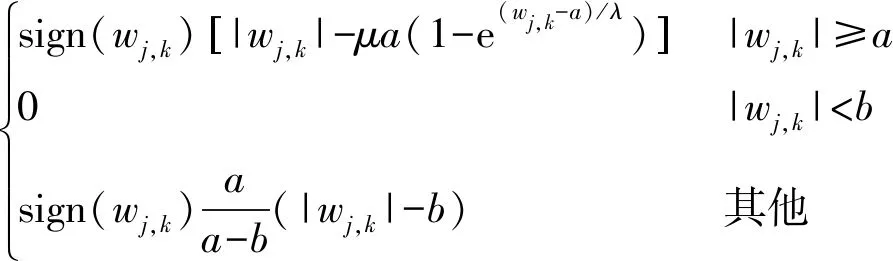
(12)

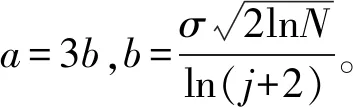
2 仿真验证

2.1 仿真条件

以经典的测试信号——Blocks信号和HeaviSine信号进行仿真验证。分析信号的采样点数为1 024,添加白噪声,信噪比为SNR=35db,采用db5小波进行4层分解。

2.2 去噪效果评价

比较硬阈值函数、软阈值函数、新阈值函数的去噪效果,并以去噪后信号的信噪比SNR和均方根误差作为比较标准。SNR和RMSE的计算公式如下:

(13)

(14)

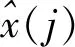
2.3 仿真效果比较

图1和图2分别是Blocks信号与HeaviSine信号的原始信号和添加白噪声后的信号。图3是Blocks信号与HeaviSine信号的硬阈值函数去噪后的信号。图4是Blocks信号与HeaviSine信号的软阈值函数去噪后的信号。图5分别是Blocks信号与HeaviSine信号的新阈值函数去噪后的信号。

图1 Blocks信号与HeaviSine信号的原始信号

图2 Blocks信号与HeaviSine信号的加噪后信号

图3 Blocks信号与HeaviSine信号的硬阈值函数去噪后的信号

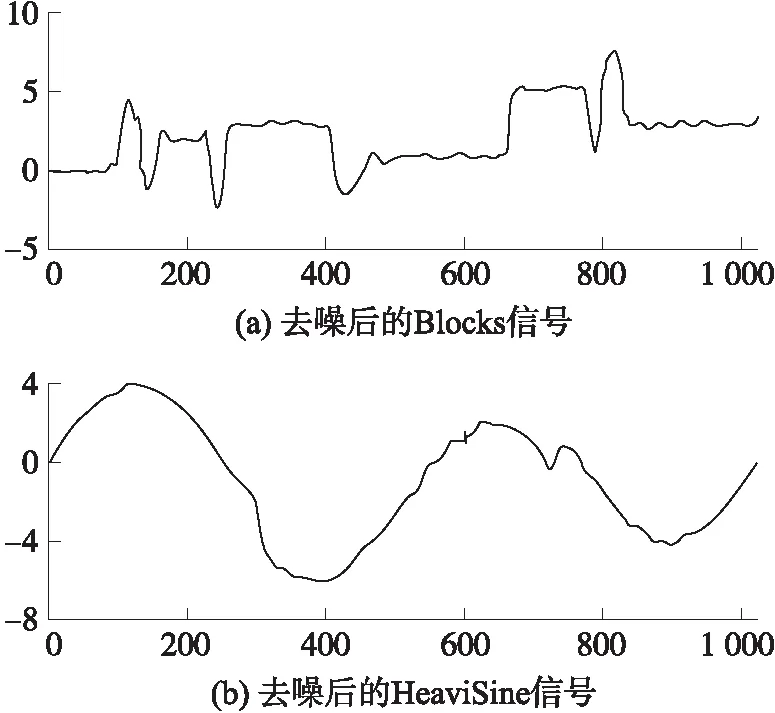
图4 Blocks信号与HeaviSine信号的软阈值函数去噪后的信号

由图1～图5对比可知:HeaviSine硬阈值去噪后的信号在横坐标600附近明显存在一个尖峰值,这个尖峰值在软阈值去噪后的信号中明显减小,在新阈值去噪后的信号中基本消失。

图5 Blocks信号与HeaviSine信号的新阈值函数去噪后的信号

由表1和表2可知,对两种信号而言,新阈值函数去噪后的信噪比优于软阈值函数和硬阈值函数,均方误差小于软阈值函数和硬阈值函数。说明新阈值函数有较好的去噪效果,这取决于新阈值函数的平滑性和自然过渡性。

由表3和表4可知,调整μ值对HeaviSine信号的信噪比与均方根误差没有影响,这是因为该信号分解的小波系数均小于3λ。观察Blocks信号的信噪比与均方根误差随μ值的变化可知,对加噪后的Blocks信号而言,μ越小,去噪效果越好。

表1 信噪比(SNR)比较

表2 均方根误差(RMSE)比较

表3 新阈值函数改变μ值的信噪比(SNR)比较

表4 新阈值函数改变μ值的均方根误差(RMSE)比较

3 实测爆炸分离试验冲击信号处理

3.1 试验简述

采用压电式加速度传感器为测量元件,搭建测试系统,图6是某爆炸分离试验中用压电式加速度传感器采集得到的实测冲击加速度信号,传感器量程选择合理,目视检查数据满足要求。提取信号有效信息前需要对数据做去噪处理和零漂检查。

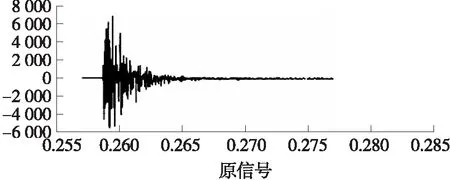
图6 实测冲击加速度信号

3.2 数据品质评估标准

依据GJB/Z222-2005《动力学环境数据采集和分析指南》,对冲击数据品质进行评估,可采用如下方法[16]:

①速度检查:对冲击加速度进行时间积分后,正常波形应表现为在零值附近振荡,之后应衰减为零;无效数据往往会有速度漂移现象。去掉噪声引起的趋势项后,若积分速度与结构的速度之比大于2∶1,则认为数据无效;

②冲击响应谱检查:正常的爆炸冲击数据有相似的冲击响应正谱和负谱,无效的数据则差异较大。为进一步衡量正负谱线重合度,以正负谱线互相关系数为依据[17]:

(15)

其中Cov(SRS+,SRS-)为正负响应谱相关函数,Var(SRS+)和Var(SRS-)分别为正负响应谱方差。

图7 原信号冲击响应谱正负谱线图及原信号积分后速度信号

3.3 数据分析

如图7,对原始数据做冲击响应谱分析,可以看出在中低频段正负谱线相差较大,说明信号中混有低频噪声干扰。对原始数据做速度积分检查,积分信号偏离零值,存在明显的零点漂移现象。原始数据需要进行去噪处理后再加以分析。对原信号采用db8小波基函数做8层分解分别利用3种阈值函数进行去噪处理[18]。

由图8～图10可知:3种阈值函数去噪后,积分后的速度信号均满足在零值附近震荡后回零的要求,冲击响应谱的正负谱线基本吻合。说明使用小波阈值去噪方法,可以有效去除冲击加速度信号中的噪声分量,重构信号消除了基线漂移并保留了信号的有效成分。

图10 新阈值函数去噪后的冲击响应谱正负谱线图及积分后速度信号

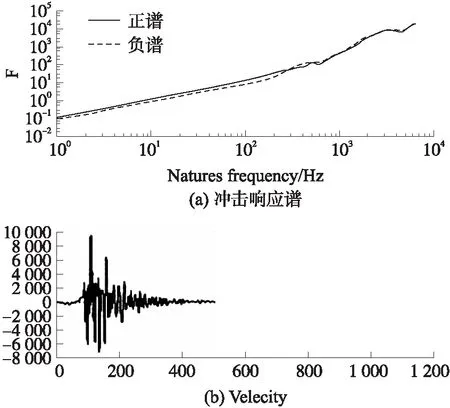
图8 硬阈值函数去噪后的冲击响应谱正负谱线图及积分后速度信号

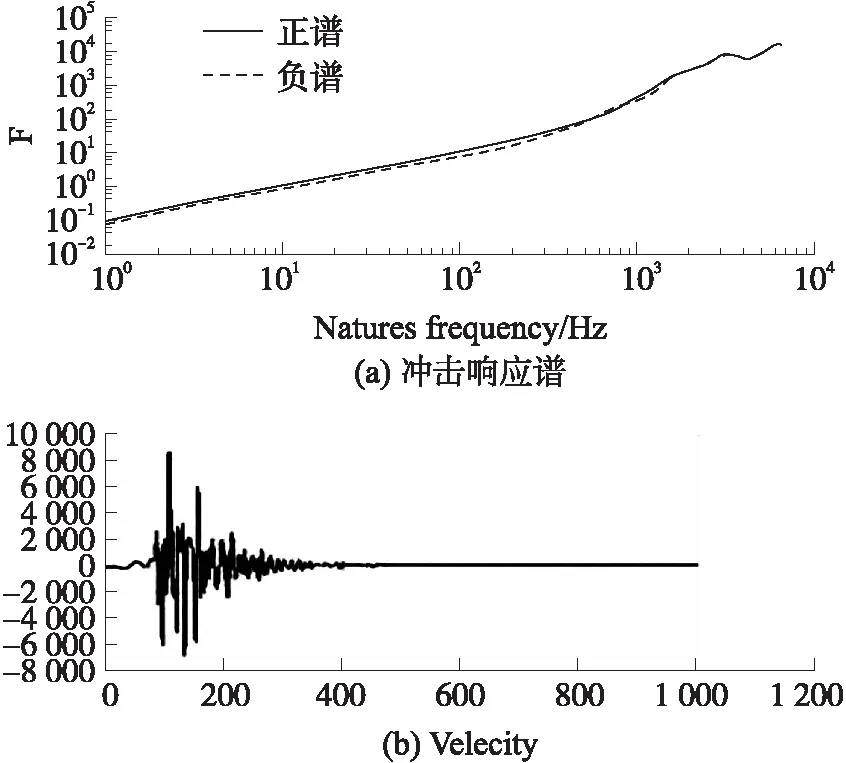
图9 软阈值函数去噪后的冲击响应谱正负谱线图及积分后速度信号

原信号硬阈值软阈值新阈值速度积分不对称对称且回零对称且回零对称且回零srs正负谱线不一致基本一致基本一致基本一致互相关系数0.756 20.970 20.971 70.999 7

由表5中的正负谱线互相关系数可知:3种阈值函数去噪后的正负谱互相关系数均有提高,新阈值函数的正负谱互相关系数达到0.999 7,明显优于硬阈值与软阈值去噪结果。

4 结论

由于受到压电式加速度传感器特性、试验环境等因素的影响,实测所得冲击加速度信号往往会含有噪声干扰和不同程度的基线漂移。小波阈值去噪是处理冲击加速度信号的有效方案,本文提出的新阈值函数及改进的变阈值方案在仿真信号以及冲击加速度信号的处理过程中均具有良好的表现,试验数据证明,该阈值函数和变阈值方案可用于处理冲击加速度信号。