基于滑模观测器的电动助力转向系统的鲁棒故障诊断
2019-04-10汤晓东范中心
罗 石, 汤晓东, 范中心
(江苏大学 汽车与交通工程学院, 江苏 镇江 212000)
0 引言
随着时代的发展和科技的进步,新能源汽车无疑成为一个重要的发展趋势,电动助力转向系统无疑是汽车上的核心部件,作为转型系统的核心部件助力电机,由于汽车复杂多变的驾驶条件和运行环境,加上电机的内部结构,容易引发各种故障.一旦出现故障,就不可避免地会产生极其严重的故障.因此,对助力电机的故障诊断和定位具有十分重要的意义.
近年来,有许多研究人员对于助力电机进行了大量的研究.蔡祥熙[1]对于助力电机的过热原因进行了分析,并且对于过热原因做了相关的分析和实验.曹艳玲等[2]对路面附着系数做了相关研究,从而完成了电机的稳定性控制.王祥等[3]则提出了用遗忘因子递推最小二乘法来完成直流电机故障诊断.Bhat R A等[4]通过对转向系统中的电机进行建模,从而完成了对电机的分析.Lee D等[5]通过对驾驶员转矩和辅助电机转矩之间一一对应的关系完成了对控制器的设计.从上面看到,对EPS系统的研究一直在进行,包括对助力电机的控制和故障诊断,上述方法在无扰动电机故障诊断中具有极好的应用效果.然而,由于汽车自身运行环境复杂,干扰因素多,传统的故障诊断方法存在一定的误差.为此,本文提出了一种应用于助力转向系统故障诊断的新方法——滑模观测器法[6,7].与传统的诊断方法相比,滑模观测器具有较强的抗干扰能力和鲁棒性.此外,本文不仅仅对于电机的状态进行观测,同时对整车状态进行了观测,保证了故障的准确度和故障的实时重构.仿真结果表明,该方法能有效地重构具有干扰的故障.
1 模型描述
1.1 执行器助力电机
电动助力转向系统的执行器是助力电机,理想情况下的电机模型如图1所示.
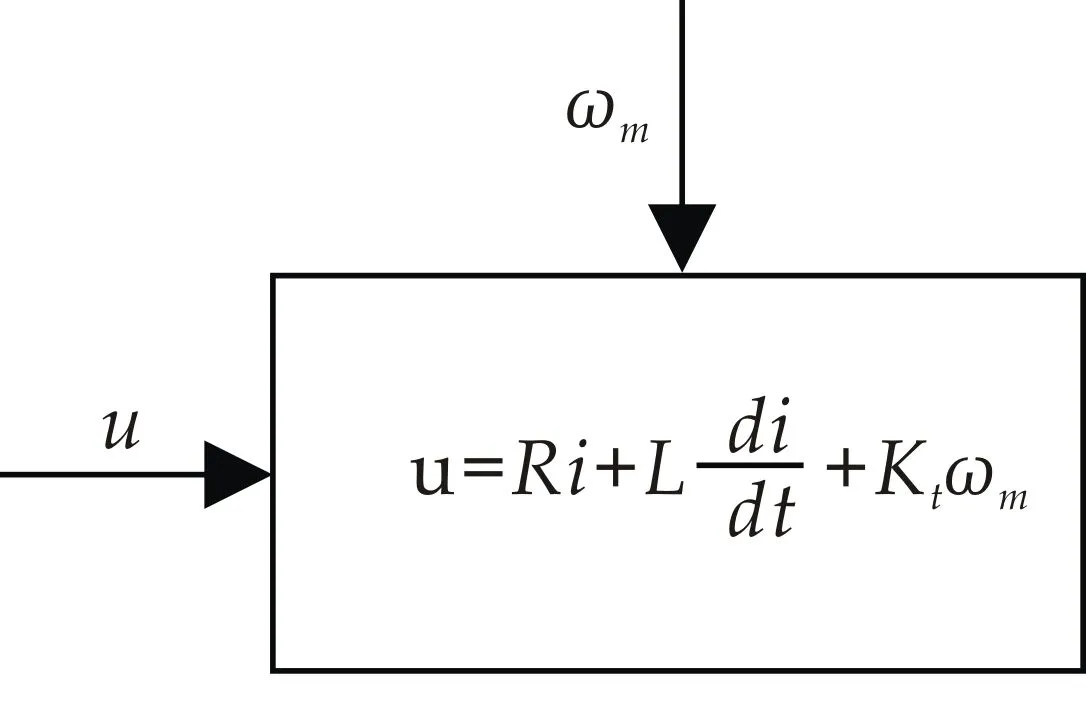
图1 助力电机模型简图

(1)
式(1)中:Jm是转动惯量,Bm是阻尼系数, 是电机转角,M是电机的输出力矩,Ms是驾驶员的手力,MH是总的转向阻力矩,R是电动机电枢电阻,Kr是电动机转动常量,i是电机电流,L是电枢电感,U是电机电压,Kt是反电动势常量.
考虑原地阻力矩模型以方向盘的转角作为输入,得到阻力矩计算模型如下[8]:
(2)
式(2)中:il为转向系统传动比;vl为助力系数;δ为车轮转角;Jω,Bω分别为转向系折算到转向轴的转动惯量和阻尼系数;M1,M2分别为轮胎拖矩和主销内倾造成的回正力矩.
电机力矩和手上力之和与转向阻力矩相等,定义手力矩和总阻力矩的关系:Ms=0.1MH.
式(1)重写为:
(3)
模型总的输入是方向盘转角,由于方向盘转角,前轮转角,电机转角成比例关系,所以根据式(3)中第一个公式计算得到助力电机的理论电流,从而得到助力电机的理论电压,根据第二个公式,助力电机的状态方程写为:
(4)
1.2 整车模型
本文以普通的二轮汽车作为研究对象,根据汽车动力学做出假设,通过合理的假设将整车模型简化成二自由度模型[9],如图2所示.

图2 二自由度模型简图
得到二自由度方程如下所示:
(5)
式(5)中:m是汽车质量;Iz为汽车绕z轴的转动惯量;ωr为横摆角速度;u为汽车车速;β为质心侧偏角;a为质心至前轴距离;b为质心至后轴距离;k1为前轮侧偏刚度;k2为后轮侧偏刚度.
将式(5)改写成:
(6)
令:
得到二自由度状态方程如下所示:
(7)
由于前轮转角、方向盘转角以及电机转角成比例,于是令:δ=Kθm
根据电机模型和整车模型将矩阵进行增广,得到所要观测的系统的模型如下所示:
(8)
2 滑模观测器的描述
对于系统8而言,同时考虑到其具有执行器故障和不确定的干扰项,于是得到:

(9)
式(9)中:
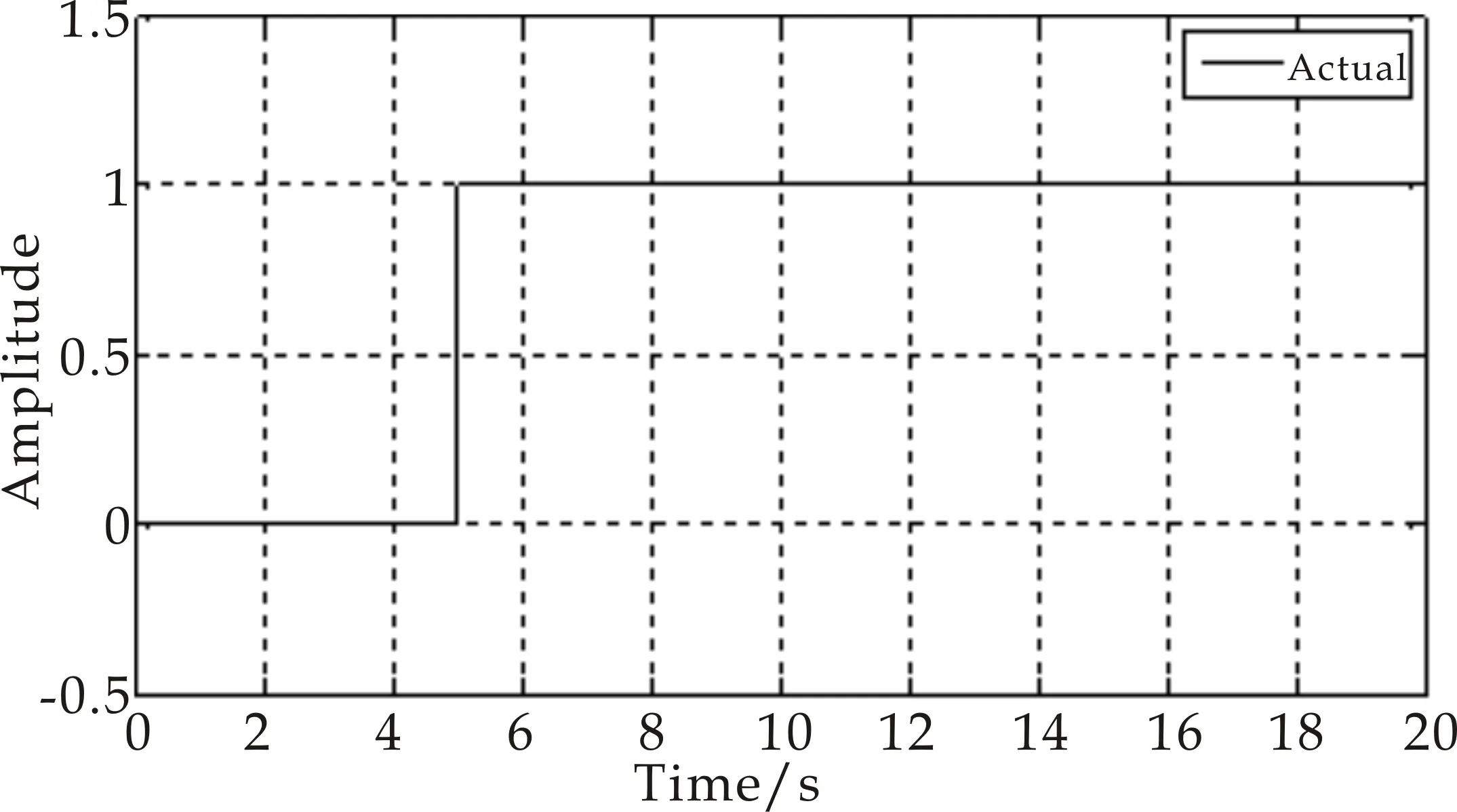
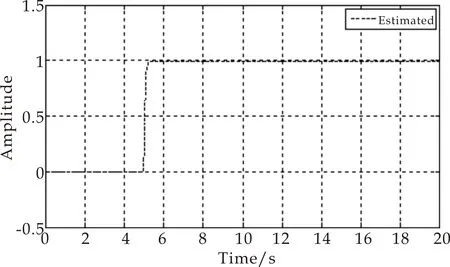
C∈Rn*p是输出矩阵,由自己定义;f(t)∈Rq为执行器故障向量,它是有界的,f(t) (10) M为故障矩阵,根据现实情况取得. 定理1rank(CM)=rank(M),所以存在坐标变换使得变换之后的三元组(A,M,C)具有以下结构: (11) 其中,T是正交矩阵[10]. 由于edwards观测器的鲁棒性能好,跟踪能力强,因此使用此类观测器,形式如下: (12) Gl,Gn∈Rn*p都是自定义的矩阵,定义: (13) 式(13)中: l0∈R(n-p)*(p-q),P0=P0T∈RP*P (14) v是所要控制的等效注入误差: (15) (16) 其中A0是由自己定义的: A0=A-GlC (17) 存在李雅普诺夫矩阵P满足: (18) 式(18)中:P0∈R(n-p)*(n-p),并且满足下式: P(A-GlC)+(A-GlC)TP<0 (19) 当标量ρ满足:ρ>‖P0CM‖m时,对于上文所提到的李雅普诺夫矩阵进行求导,得到 2‖ey‖(ρ-‖P0CM‖m) 证明了状态估计误差是二次稳定的. 同样,通过选择合适的增益使系统到达设计滑模面s={e:Ce=0}[11]. 引入新的坐标变换: 将式(11)里面的三元组进行变换,得到: (20) 式(20)中: Aa11=A11+L0A211;Mm2∈Rp*q (21) 重写滑模观测器增益,lyapunov矩阵P以及干扰矩阵Q,得到: (22) 此时,根据式(19)~(22),对状态估计误差重写,得到: (23) (24) 定义:N=[N1M0-1] 式中:N1∈Rq*(p-q) 将式(24)左乘NTT,得到: f(t)=NA21e1(t)+NTTP0-1v-NQ2ξ (25) 得到故障f(t)的表达式,定义一个准重构信号: (26) 根据式(23)、(25),重写式(26)为: MA21(sIn-p-(A11+LA21)-1(Q1+LQ2)+NQ2)ξ (27) 为了尽量减小不确定项对于重构信号的干扰,那么就要选择合适的N和L.根据有界实定理可以得到,只要满足下面这个不等式,那么从干扰信号到重构信号的传递函数 NA21(sIn-p-(A11+LA21)-1(Q1+LQ2)+NQ2) 的增益g<η∈R+[12-14]: <0 其中:H∈R(n-p)*(n-p),是对称正定的. 在满足上述不等式的基础上,同时还要选择合适的滑模观测器增益Gl,L0满足式(19). 当观测器增益选为: Gl=γ0P-1CT(DdDdT)-1 (28) L0=P11-1P121 (29) 符合上述要求[15].上述不等式可以使用lmi方法求解,具体求解方法参见文献[16]和[17]. 本文使用carsim软件对于所建立的整车模型进行验证.本文以普通的小轿车作为提取对象,传动系统,车体,动力系统,空气动力学模型都是carsim默认确定的,使用车辆参数如下:m=2 021 kg,L=2.51 m,a=1.2 m,b=1.31 m,k1=-65 000 N/rad,k2=-55 000 N/rad. 仿真实验条件:车辆行驶在附着系数为0.85的路面上,车速u=40 km/h,carsim设置方向盘转角输入如图3所示,仿真对比结果如图4所示. 图3 方向盘转角输入 图4 模型对比图 二自由度模型忽略了一些相关扰动以及一些汽车动力学因素,因此carsim的响应有些微的区别,但整体走势是一致的,所增广的矩阵当中的二自由度模型符合要求,二自由度模型可用. 电机参数如下所示: Jm=0.06 kg·m2,Bm=0.01 Nms/rad,L=0.002 9 H,kr=0.065 Nm/A,kt=0.06 Vs/rad,R=0.168 Ω. 式(8)中,各分布矩阵为: 矩阵C自定义的,这里选择输出为电机电流和汽车的横摆角速度,得到: 4.2.1 干扰矩阵Q的选择 控制系统的干扰有许多,有地面附着系数变化导致的负载扰动,有工作温度导致元件变化的热扰动,也有元件老化导致的电噪声和传动系摩擦引起的摩擦噪声.此时这个模型的扰动是汽车前后轴的变化以及整车质量的变化,得到扰动矩阵如下所示[18]: 从而得到: 4.2.2 故障矩阵M的选择 执行器故障分为执行器卡死,执行器恒增益变化和执行器恒偏差失效三种,本文研究的是第三种故障,表现为电机转速的变化,仿真信号用一个阶跃信号来表示,综合考虑模型以及现实情况,选择故障矩阵: 在5 s的时候假设电机转速出现问题,由故障矩阵的选择得知,用一阶跃信号代替,如图5所示,观测器结果如图6所示. 图5 故障信号 图6 故障重构信号 通过仿真实例看到观测器很好的实时监测了并且重构了这个故障信号. 本文针对电动助力转向系统在不确定干扰下可能出现的故障进行了分析,并且通过滑模观测器实现对故障的检测以及重构.结果显示,在存在参数摄动以及干扰项的情况下,滑模观测器依然可以很好的重构出故障,将这种方法运用在电动助力转向系统上是可行的,并且具有抗干扰能力强的优点.3 鲁棒故障重构

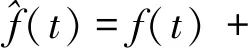
4 仿真结果
4.1 模型的验证
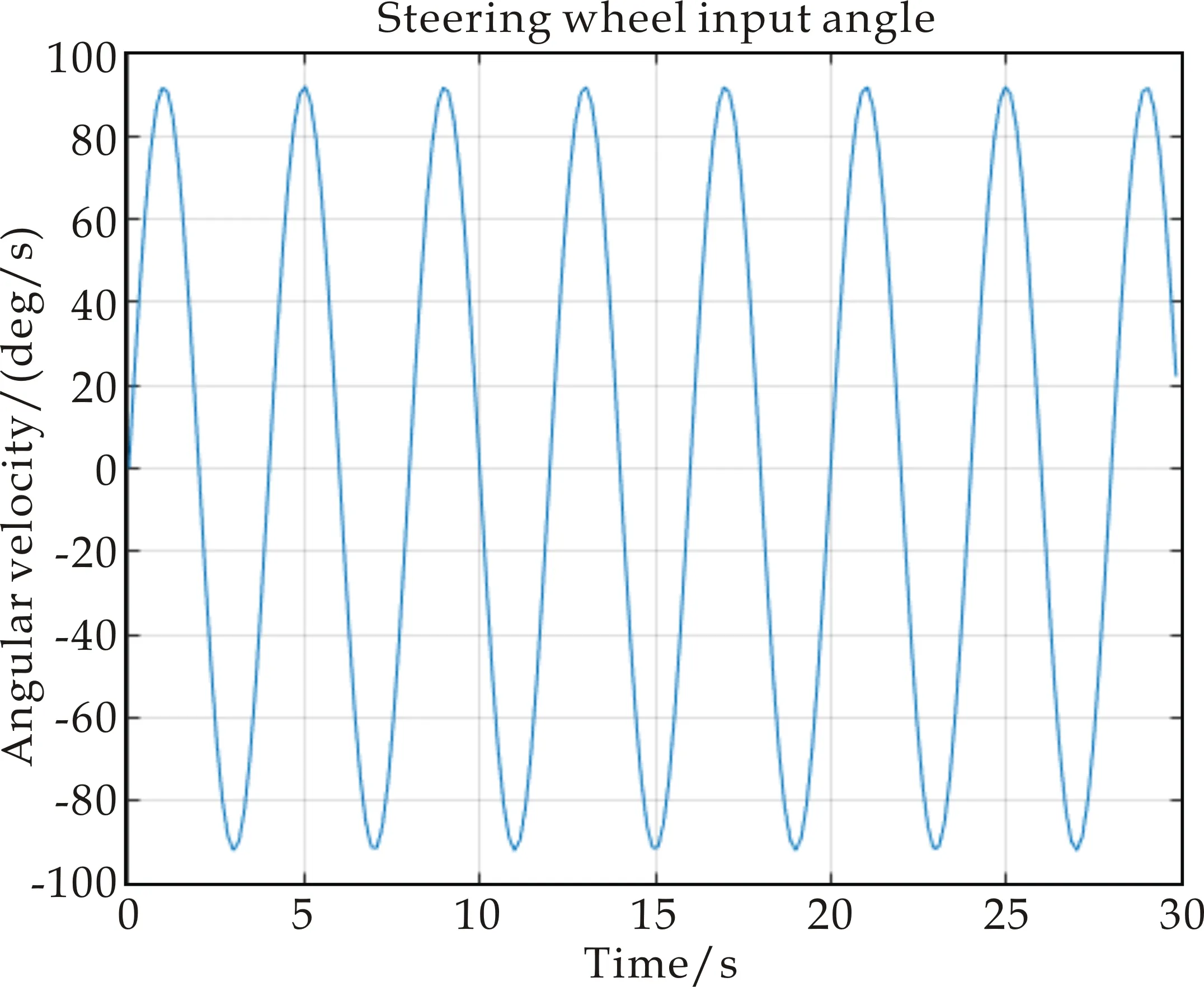
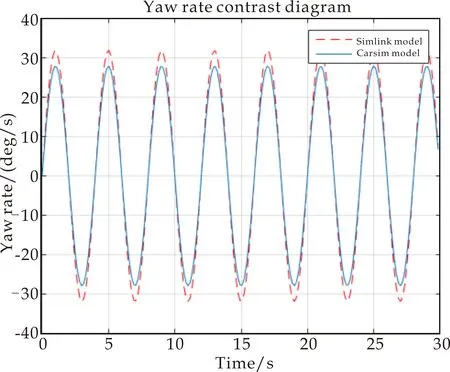
4.2 鲁棒故障重构仿真算例




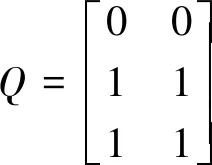

5 结论
