人力资本异质性对中国金融业全要素生产率的影响※——基于空间面板模型

徐旭初 徐家楠

（安徽财经大学，安徽 蚌埠 233030）

党的十九大报告中明确提出，中国的经济已经进入了由高速增长转向高质量发展的新时代。高效的金融体系能提升经济发展质量，达到经济转型的需要。而金融业全要素生产率是评价金融发展水平和效率的重要指标，因此自上世纪90年代起金融业全要素生产率成为学者的研究重点。人力资本投入对金融业全要素生产率的产生重要影响。研究人力资本对金融业的全要素生产率影响不能只看人力资本的整体，而要考虑人力资本的异质性，因为不同的人力资本会产生不同的影响。因此从理论和实证的角度研究人力资本的异质性对金融业全要素生产率产生怎么的作用。这对促进金融业发展具有重要的现实意义和理论意义。

一、文献综述

新经济增长理论是研究人力资本与全要素生产率关系的理论基础，认为人力资本和技术进步是提高全要素生产率的两大动力。就影响理论上的影响机制而言，Benhabib and Spiegel（1994）[1]认为人力资本主要通过两种途径对全要素生产率产生影响。第一是随着人力资本的存量增加，使得一国的技术创新能力得到增强，从而提高一国的全要素生产率。第二是目前世界各个国家在各个方面相互联系，人力资本通过对发达国家进行技术模仿和技术追赶，最终影响全要素生产率。

大量文献表明人力资本对全要素生产率具有增长效应。Coe et al．[2]（2009）利用动态最小二乘法对1971年到2004年的24个OECD国家的面板数据进行分析，结果发现人力资本提高全要素生产率。王文静等（2014）[3]利用中国30个省份1978年到2009年的面板数据，并建立空间Benhabib-Spiege模型研究人力资本与全要素生产率的关系，实证结果表明人力资本的平均水平提高了全要素生产率。邓翔等（2018）[4]利用中国30个省份2000年到2014年的面板数据，基于SBM-Undesirable模型和Global Malmquist Luenberger指数法分析人力资本对全要素生产率的影响，实证结果表明提高人力资本水平将促进全要素生产率的提高。但是也有一部分学者认为人力资本不会提高全要素生产率。Pritchetl（2001）[5]认为教育的扩张不利于全要素生产率的提高。尹朝静（2017）[6]利用中国1978年到2012年省级面板数据研究农村人力资本对农村全要素生产率的影响，结果发现农村人力资本能够提高农村全要素生产率，但是影响比较小。还有一些学者研究人力资本的异质性对全要素生产率的影响。Vandenbussche等（2006）[7]研究发现人力资本的平均水平对全要素生产率无影响，只有高等人力资本才能促进全要素生产率的提高。韩海彬等（2014）[8]利用中国农村1993年到2010年的面板数据研究发现初等人力资本有利于增强农业全要素生产率，中等人力资本则不会影响全要素生产率，高等人力资本则阻碍了全要素生产率的提高。

从文献分析出近年来存在大量关于人力资本与全要素生产率之间关系的研究，但是鲜有文献分析人力资本的异质性对金融业全要素生产率的影响。本文以人力资本为基础，将人力资本分为初等人力资本，中等人力资本和高等人力资本三大类，测算30个省份的金融业全要素生产率的基础上，不但构建静态面板模型，而且通过加入地理空间因素，建立空间面板模型，实证检验了人力资本的异质性在空间上对金融业全要素生产率的影响，从而为提高金融业全要素生产率，促进金融发展提供理论和实证依据。

二、模型介绍

（一）空间相关性分析

空间相关性检验是建立空间计量模型的基础，如果检验通过则建立空间模型，否则使用标准的计量模型。检验空间相关性的方法具有多样性，而目前比较流行的方法是莫兰指数。莫兰指数包括全局Moran’s I和局部 Moran’s I。全局 Moran’s I的公式：

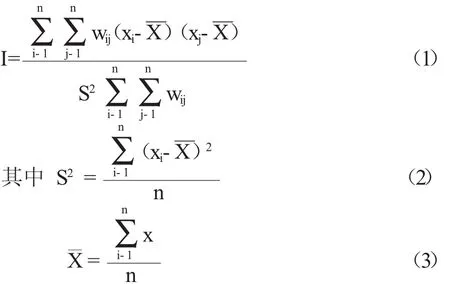
莫兰指数的取值在-1和1之间，当莫兰指数大于0时，此时各地区在空间上存在正相关，反之，各地区在空间上存在负相关，而莫兰指数为0时，各地区在空间不存在相关性。莫兰指数越接近1或-1时，空间相关性就越强。

局部Moran’s I的公式：

局部Moran’s I与全局Moran’s I的定义具有相似性。莫兰指数散点图能够反映这种现象，莫兰指数散点图的第一象限反映高值与高值，第三象限反映低值与低值，这两个象限说明存在正相关，而第二象限反映高值与低值，第四象限反映低值与高值，这两个象限说明存在负相关。

（二）空间权重矩阵

本文选用0-1矩阵作为本文的空间权重矩阵，0-1矩阵的编制是根据两个地区是否相邻来确定的，即当第i地区和第j地区相邻时，Wij等于1，反之等于0。

（三）空间计量模型

传统的计量模型没有把各地区联系在一起，而是单独进行分析，空间计量模型则克服这一缺点，把各地区进行联系，这也是空间模型与传统的模型的主要的不同之处之一。本文使用空间自回归模型（SAR）和空间误差模型（SEM）分析金融业全要素生产率在空间上的效应。

空间自回归模型（SAR）主要是研究邻近地区的金融业全要素生产率对本地区的金融业全要素生产率的空间效应。SAR模型如下：

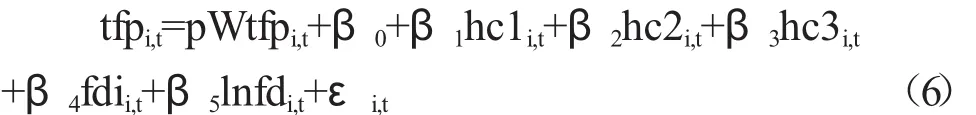
其中β0为常数项，β为回归系数，HC1、HC2、HC3、FDI、FD分别初等人力资本、中等人力资本、高等人力资本、实际利用外商直接投资额/GDP和金融机构本外币存贷款余额/GDP，i为中国各地地区，t为各个年份，W为空间权重矩阵，p为空间自回归系数，反应金融业全要素生产率的依赖程度，即邻近地区的金融业全要素生产率对本地区的金融业全要素生产率空间溢出效应。

空间误差模型（SEM）主要是研究邻近地区的各个解释变量误差本地区的金融业全要素生产率的空间效应。SAR模型如下：

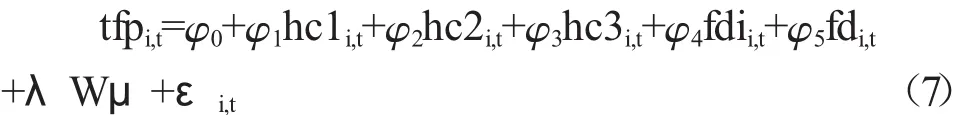
其中 φ0为常数项，φ 为回归系数，HC1、HC2、HC3、FDI、FD分别初等人力资本、中等人力资本、高等人力资本、实际利用外商直接投资额/GDP和金融机构本外币存贷款余额/GDP，i为中国各地地区，t为各个年份，W为空间权重矩阵，λ为空间误差系数，主要反应邻接地区的各个解释变量的的误差冲击对本区域金融业全要素生产率的空间效应。

三、数据来源和变量选择

（一）数据来源

本文选取2004年到2016年30个内地省份（除西藏外）的面板数据为样本，其中全社会固定资产投资，城镇单位就业人员，金融业增加值来自国家统计局和中国经济大数据平台，各地区受教育程度来自中国人口和就业统计年鉴，实际利用外资、金融机构本外币存款和金融机构本外币贷款来自Wind数据库和各省统计年鉴。

（二）变量选择

1.被解释变量

金融业全要素生产率（TFP）：本文使用DEA模型测算30个省份的金融业全要素生产率。在金融业投入产出指标上借鉴施卫东等（2013）[9]所使用指标，选取资本存量和城镇单位就业人员作为投入指标，金融业增加值作为产出指标。资本存量无法直接得到，因此本文选取永续盘存法进行资本存量的计算。

K代表资本存量，σ为折旧率，本文选取单豪杰所使用的10.96%，Z为固定资产投资指数，并换算为2000年的固定资产投资指数，T为全社会固定资产总额，从而得各个年份的资本存量。

2.解释变量

人力资本（HC）：本文使用受教育年限衡量人力资本，并按照不同的受教育年限将人力资本分为初等人力资本、中等人力资本和高等人力资本。根据胡海洋（2018）[10]估算的受教育年限的方法，本文将不同的受教育水平按照一定的受教育年限的比例进行计算（未上学0年，小学6年，初中9年，高中12年，大专15年，大学本科16年，研究生及以上19年），但是2015年以后新出现高等职业教育和中等职业教育分类，本文将其分别归为大专和高中分类中，然后相应乘以教育水平的比例，得到人力资本水平。其中由未上学和小学的受教育水平得到的人力资本为初等人力资本（HC1），由初中和高中的受教育水平得到的人力资本为中等人力资本水平（HC2），最后由大专以及以上的受教育水平得到的人力资本为高等人力资本为高等人力资本（HC3）。

控制变量：由于金融业全要素生产率还受到其他因素的影响，为了提高模型的准确度，添加了实际利用外商直接投资额（FDI）占GDP的比率和金融机构本外币存贷款余额占GDP（FD）的比率两个控制变量。

四、实证分析

（一）金融业全要素生产率测度

本文使用DEA-Malmquist方法对金融业全要素生产率进行估算，表二是TFP测算的结果。

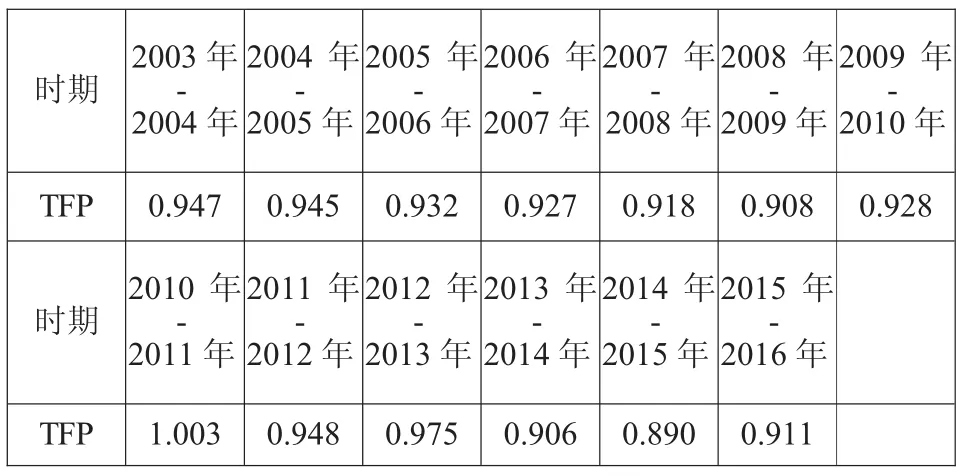
表1 2003-2016全国金融业全要素生产率测算结果

从表2可以看出，金融业TFP 2003年到2009呈现出下降趋势，2009到2011年出现上升趋势，但是2011年到2012年有所下降，2012年到2013年有所上升，2014年到2015下降，2015年到2016年出现上升趋势。这种情况的出现可能原因是各地区的经济和金融发展情况不同和本文所使用的投入变量的影响。

（二）空间相关性分析

本文使用莫兰指数对2004年到2016年的金融业全要素生产率进行检验，结果表明大部分年份的金融业全要素生产率的莫兰指数的数值在10%的水平下显著为正。从而说明30个省份的金融业全要素生产率具有显著的相关性，这就得出这30省份的金融业全要素生产率在空间存在集聚性，较高地区的金融业全要素生产率会对临近地区产生一定的聚集作用，各个地区相互影响。

为了进一步的展示金融业全要素生产率的空间集聚高低程度，本文利用Moran’sI散点图对金融业全要素生产率进行局部空间自相关分析。由于局部空间相关性测算的数据较大，因此本文只描述了2006年和2012年的金融业全要素生产率的Moran’s I散点图。如图1和图2。

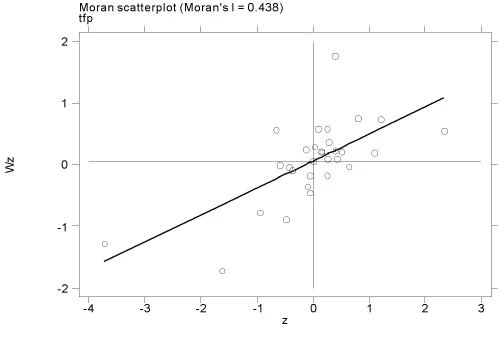
图1 2006年的金融业全要素生产率的Moran’s I散点图

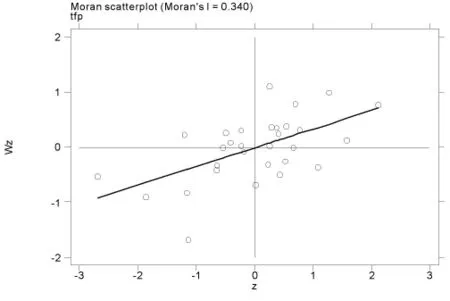
图2 2012年的金融业全要素生产率的Moran’s I散点图

从两个图中可以看出，大部分省份的金融业全要素生产率都处于第一和第三象限，因此具有正向的空间集聚关系。

通过全局Moran’s I和局部Moran’s I对金融业全要素生产率的空间相关性的分析，各地区在空间上存在空间集聚效应。

（三）静态模型和空间面板模型

本文使用Hausman检验确定使用随机效应还是固定效应模型。根据Hausman检验结果，模型一的Chi2的值为23.86，相对应的P值为0，而模型二Chi2的值为11.32，相对应的P值为0.0453，两个模型在10%的显著性水平下均拒绝原假设，因此模型一和模型二均采用固定效应的面板模型。表三为模型的回归结果。

表2 静态面板和空间面板模型的估计结果

在静态面板模型中，高等人力资本和实际利用外商直接投资对金融业全要素生产率产生显著的正向影响，而初等人力资本和中等人力资本有利于金融业全要素生产率的提高，但不显著，金融机构本外币存贷款余额之和不利于融业全要素生产率的提高，但不显著。静态面板模型忽视了地区之间的空间性，因此不再详细描述，本文重点描述空间计量模型。

在SAR模型中，模型三和模型四空间自回归系数（0.3）均在10%的显著性水平下通过检验，说明周边地区金融业全要素生产率对本地区产生促进作用，即邻近地区的金融业全要素生产率每增加1%将会使得本地区的金融业全要素生产率提高0.3%，从而说明中国各省的金融业全要素生产率的空间竞争效应小于空间溢出效应。在SEM模型中，模型五和模型六空间误差系数（0.223和0.207）均在10%的显著性水平下通过检验，说明周边地区的初等人力资本，中等人力资本和高等人力资本对本地区的金融业全要素生产率产生正向的空间溢出效应。检验结果与莫兰指数的检验结果相一致，从而说明建立空间计量模型的正确性。

在不考虑控制变量的情况下，模型三和模型五中初等人力资本和中等人力资本的系数估计值在10%的显著性水平下均不显著但为正，从而说明初等人力资本和中等人力资本均有利于提高金融业全要素生产率，但影响效应比较小，这可能由于金融业对于从业者的受教育的要求比较高，低教育程度的从业者很少在金融业中工作。高等人力资本的系数估计值在10%的显著性水平下显著且为正，从而说明高等人力资本将会对金融业全要素生产率产生显著的正向影响，这与静态面板模型的估计结果具有一致性。这分析的结果与目前中国金融业的情况具有一致性。

在考虑控制变量的情况下，模型四和模型六控制了实际利用外商直接投资额和金融机构本外币存贷款余额之和以后，初等人力资本和中等人力资本仍然有利于促进金融业全要素生产率的增加，但系数的估计值变小，影响的效果进一步下降，同时高等人力资本对金融业全要素生产率仍然具有正向显著作用，但系数估计值同样有所下降。这与静态面板模型的估计结果具有一致性。这可能是由于控制变量加入所带来的影响，使得影响效果下降。实际利用外商直接投资额回归系数为正，但是不显著，从而说明实际利用外商直接投资额有利于金融业全要素生产率具提高但是不显著。这与静态面板模型有所差异，这可以由于实际利用外商直接投资在中国各地区的差异性。金融机构本外币存贷款余额之和的系数估计值在10%的显著性水平下不显著但为负，从而说明金融机构本外币存贷款余额之和不利于金融业全要素生产率提高，但影响效应比较小，这可能是因为一方面中国金融业中金融机构存贷款会对金融业的全要素生产率产生促进作用，但是另一方面中国金融业中金融机构存贷款过多，使得直接投资减少，金融市场的自我调节的资金变少，从而导致金融业效率变低。结果与静态面板模型具有一致性。

五、结论与建议

本文基于DEA-Malmquist方法测算金融业全要素生产，进而建立静态面板模型和动态面板模型研究人力资本异质性与金融业全要素生产率之间的关系，结果发现：（1）中国各地区的金融业全要素生产率具有空间相关性，邻近地区的金融业全要素生产率将对本地区的金融业全要素生产率产生正向的空间溢出效应。（2）初等人力资本和中等人力资本有利于提高金融业全要素生产率，但是产生的影响效应低。高等人力资本对金融业全要素生产率产生显著的正向空间溢出效应。显然异质性人力资本存在差异。（3）实际利用外商直接外资有利于全要素生产率的提高，而金融机构本外币存贷款余额则对全要素生产率的提高产生负向作用，但是影响作用小。

从上述分析中，提出以下建议：（1）中国各地区应该加强联系，消除各地区的金融业的差异性，使得各地区的金融业平衡发展，最终促进金融业的发展。（2）加强教育投入，建立高水平的教育制度，培养高等级的人才，促进人力资本的提高，同时注意各地区人力资本发展的均衡性，考虑人力资本在空间上的相关性，发挥邻近地区人力资本的作用。（3）提高实际利用外商直接外资水平，减少金融机构本外币存贷款余额，发挥金融市场作用。