无双线性映射的无证书签密方案

高改梅， 彭新光， 秦泽峰

(1. 太原理工大学 信息与计算机学院， 山西 太原 030024；2. 太原科技大学 计算机科学与技术学院， 山西 太原 030024；3. 山西青年职业学院 计算机系， 山西 太原 030032)

0 引 言

无证书公钥密码体制[1](CL-PKC, Certificateless Public Key Cryptography)解决了传统公钥密码体制[2]的复杂证书管理问题和基于身份密码体制[3]的密钥托管问题， 提高了密码系统的运行效率. CL-PKC中用户的私钥由自己和密钥生成中心(KGC， Key Generation Center)共同生成. 因此， 用户私钥不由KGC完全掌控， 减少了对第三方KGC的依赖.

签密[4](SC， Signcryption)在一个逻辑步骤内同时对信息进行签名和加密， 与传统的“签名”+“加密”方式相比， SC降低了计算量和通信开销. 文献[5-6]把签密引入身份认证和数据访问控制中， 以提高信息安全运行机制的效率. 2008 年， Barbos等人[7]首次将签密机制引入CL-PKC中， 提出基于双线性映射理论的无证书签密机制(CLSC, Certificateless Signcryption)， 但未进行安全性证明. 由于双线性对运算的计算成本是点乘运算计算成本的20倍[8]， 所以基于双线性对的CLSC计算开销较高. Liu等人[9]提出了无双线性对运算的CLSC(LX-CLSC)， 并在随机预言模型中， 基于计算Diffie-Hellman假设和离散对数困难问题证明了该方案的机密性和认证性， 同时进行了效率分析. 2013年， Zhou等人[10]发现LX-CLSC方案不满足机密性和不可伪造性， 安全证明中也存在缺陷， 提出改进的无双线性对运算的CLSC(ZW-CLSC). 同时证明了所提方案的安全性， 并进行了效率分析. 2014年， Shi等人[11]又提出一种改进的无双线性对运算的CLSC(SKGZ-CLSC)， 并对其进行了密码学分析， 证明该机制是可证安全的. 2016年， Zhou等人[12]提出一种安全高效的CLSC(ZYZ-CLSC)， 并证明了方案的安全性， 通过性能分析指出其方案计算效率更优.

本文首先对ZW-CLSC方案进行正确性分析， 指出ZW-CLSC方案在解签密阶段根据已知信息无法恢复出明文消息. 同时构造具体的攻击实例， 验证ZW-CLSC方案无法抵抗其所声称的对类敌手的不可伪造性攻击. 另外， 分析发现SKGZ-CLSC方案和ZYZ-CLSC方案的计算开销较高. 因此， 本文设计了改进的无双线性映射的无证书签密方案GPQ-CLSC. 首先对ZW-CLSC方案进行安全性分析， 然后详细阐述GPQ-CLSC方案， 并进行正确性分析， 接着在随机预言模型中证明GPQ-CLSC方案的机密性和不可伪造性， 最后是效率分析.

1 基础知识

1.1 相关困难性问题

定义1 计算Diffie-Hellman(CDH， Compute Diffie-Hellman)

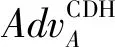
定义2 离散对数(DL, Discrete Logarithm)

设G是椭圆曲线上阶为q的循环群，P是G的生成元. 给定二元组(P,uP)， DL问题的目的是计算u.

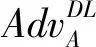
1.2 CLSC安全模型

CLSC方案的攻击敌手分为A1和A2两类[13]：

A1类敌手是恶意用户， 此类敌手不能掌控系统主密钥， 但可随意替换用户公钥.

A2类敌手是恶意KGC， 此类敌手可掌控系统主密钥， 但不能随意替换用户公钥.

安全的CLSC方案至少满足IND-CLSC-CCA2攻击(indistinguishability certificateless signcryption adaptive chosen ciphertext attacks)下的机密性和EUF-CLSC-CMA攻击(existential unforgeability certificateless signcryption chosen message attack)下的不可伪造性， 详细的安全模型和游戏定义见文献[13].

2 ZW-CLSC方案的安全性分析

本节对ZW-CLSC方案进行分析， 指出其不满足正确性. 并构造具体的攻击实例， 证明ZW-CLSC方案无法满足其所声称的不可伪造性.

2.1 不满足正确性

在解签密阶段， 用m‖s=H3(VB)⊕C恢复出m‖s， 无法从m‖s推断出m的值， 因为m和s的长度不是固定值. 例如， 计算出H3(VB)并且得到m‖s=101001010010011011010001， 但是由于不知道m和s的消息空间大小， 无法确定m的值为m=101还是m=101001.

2.2 不可伪造性攻击

设Alice和Bob分别是ZW-CLSC方案的发送方和接收方， Alice的公私钥分别是PKA=(RA,XA)和SKA=(DA,xA). Bob的公私钥分别是PKB=(RB,XB)和SKB=(DB,xB).

A1类敌手Eva掌握了Alice的公钥PKA， Eva代替Alice与Bob进行消息交互， 过程如下：

1) 敌手Eva伪造公钥

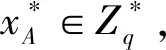
2) 敌手Eva伪造Alice的签密文

② 计算VA=a(RB+XB+h1y)和U=H4(VA)P.

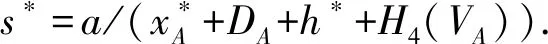
④ Eva发送签密文δ*=(T,C*,U)给Bob.

3) Bob验证签密的合法性

Bob收到签密文后， 根据解签密算法验证签密的合法性. 若验证成功， 则Eva成功伪造了Alice的合法签密； 否则， Eva伪造失败. 具体验证过程如下：

① 计算VB=(xB+DB)T.

② 恢复消息m‖s*=H3(VB)⊕C*.

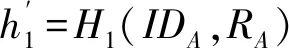
由此可知， Eva成功伪造Alice的签密， 并通过了接收者Bob的验证， 所以类敌手Eva具有伪造Alice合法签密的能力.

3 本文GPQ-CLSC方案

3.1 方案描述

GPQ-CLSC方案包括五个算法， 详细描述如下：

1) 系统建立(Setup)

KGC执行如下操作完成系统建立， 并输出系统参数.

① 输入安全参数k.

② 选择阶为大素数q的椭圆曲线循环群G，P是G的一个生成元.

⑤ 保密主密钥z， 公开系统参数params=(G,q,P,y,H1,H2,H3).

2) 部分密钥生成(PartialKeyGen)

用户IDi和KGC交互完成部分密钥生成， 描述如下：

①IDi发送身份标识给KGC.

③ KGC通过安全渠道将(di,Ri)发送给IDi. 其中di是用户的部分私钥，Ri是用户的部分公钥.

3) 用户密钥生成(KeyGen)

用户IDi收到KGC发送的部分密钥(di,Ri)后， 执行如下操作， 完成密钥的生成.

② 设置PKi=(Ri,Xi)为用户公钥， 设置SKi(di,xi)为用户私钥.

设本文的签密发送者为Alice， 其身份标识是IDA， 那么她的公钥为PKA(RA,XA)， 私钥为SKA=(dA,xA). 签密接收者为Bob， 其身份标识是IDB， 他的公钥为PKB=(RB,XB)， 私钥为SKB=(dB,xB).

4) 签密(Sign)

当Alice要发送消息m给Bob时， Alice根据Bob的身份标识IDB和公钥PKB， 并结合自己的私钥SKA进行如下操作：

② 计算VA=β(XB+RB+h1y)和h1=H1(IDB,RB).

③ 计算

h=H2(m‖T‖IDA‖IDB‖XA‖XB).

④ 计算s=(xA+β)/(h+dA+xA).

⑤ 计算C=H3(VA)⊕(m‖s).

Alice将签密文δ=(s,C,T)发送给Bob.

5) 解签密(UnSign)

当Bob 收到Alice发送的签密文后， 利用Alice 的身份标识IDA和公钥PKA， 并结合自己的私钥SKB执行如下操作进行验证.

① 计算VB=(xB+dB)T.

② 恢复消息m‖s=H3(VB)⊕C.

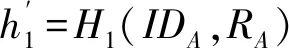
3.2 正确性分析

1) 部分密钥的正确性

Alice和Bob可通过式(1)来验证KGC为其生成的部分密钥的正确性.

Ri+H1(IDi,Ri)y=riP+zPH1(IDi,Ri)=

(ri+zH1(IDi,Ri))P=diP.

(1)

2) 密文的正确性

在UnSign算法中， 密文的验证可以通过式(2)和式(3)完成. 首先计算VB，

VB=(xB+dB)T=

(xB+rB+zH1(IDB,RB))βP=

β(XB+RB+yH1(IDB,RB))=VA.

(2)

根据VB和Alice发送的密文， Bob通过式(3)验证密文的正确性.

m‖s=H3(VB)⊕C=

H3(VB)⊕H3(VA)⊕(m‖s)=

H3(VA)⊕H3(VA)⊕(m‖s)=m‖s.

(3)

3) 签密的正确性

在UnSign解签密算法中， 签密的正确性可通过式(4)来验证.

xAP+βP=XA+T.

(4)

4 安全性分析与比较

4.1 机密性分析

定理1A1类敌手的机密性.

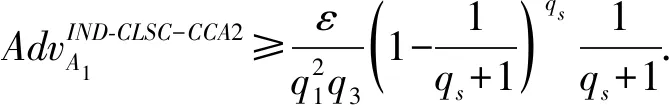
证明假设算法F以三元组(P,aP,bP)为CDH问题的挑战实例， 以Type-I敌手A1为挑战者， F的目标是计算abP. 游戏开始后， F维护列表L1,L2,L3,LD,LSK,LPK,LS,LU分别跟踪A1对预言机H1,H2,H3， 部分密钥生成， 私钥生成， 公钥生成， 签密和解签密的询问. 此外， F维护列表Lrec来记录挑战者身份信息. 各列表初始均为空.

1) 系统建立

F运行Setup算法， 并发送系统参数params给A1. F也可运行部分密钥生成、 密钥生成、 公钥查询、 公钥替换、 签密和解签密等操作.

2) 询问阶段

A1可执行多项式有界次的下列询问.

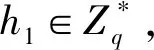
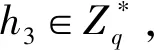
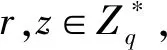
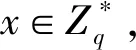
公钥生成询问： 当收到A1的请求(ID,R.X)时， F进行下述操作：

如果(ID,R,X)在LPK中已经存在， 则F将(R,X)返回给A1.

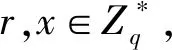
公钥替换询问： 当收到A1的替换请求(ID,R′,X′)时， F将(R′,X′)替换现存的公钥(R,X).

签密询问： 当收到A1提供的(IDA,IDB)和明文消息m时， F在列表L1中查询(IDA,RA)， 并执行下列操作：

如果c=0， F根据IDA和IDB从列表LSK和列表LPK中分别获得(IDA,dA,xA)和(IDB,RB,XB)， 然后执行Sign算法完成对明文消息m的签密， 并将签密文δ=(s,C,T)发送给A1.

如果c=1， F失败并退出.

解签密询问： 当收到A1提供的(IDA,IDB)和密文δ=(s,C,T)时， F在列表L1中查询(IDB,RB)， 并执行下列操作：

如果c=0， F根据IDA和IDB从列表LPK和列表LSK中分别获得(IDA,RA,XA)和(IDB,dB,xB)， 然后执行UnSign算法完成解签密验证， 并将解签密得到的消息m发送给A1.

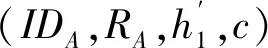
3) 挑战阶段

4) 猜测阶段

A1执行多项式有界次询问后输出其猜测值c′∈{0,1}. 如果c′=c，A1使用V′=β(XB+RB+hy)进行H3询问. 此时， CDH问题的备选答案已经存储在列表L3中. F忽略A1的猜测值， 从列表L3中随机选择V′， 输出(V′=(xB+rB)T*)/k=zβP作为CDH问题的解， 其中xB,rB,T*,V′都是未知量. 否则， F没有解决CDH问题.

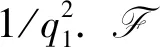
定理2 A2类敌手的机密性.

证明该定理的证明思路和方法与定理1类似， 重复部分不再赘述， 主要不同如下：

1) 敌手A2可以替换系统主秘钥z.

2) 在公钥生成询问中， 设置R=zP而不是定理1中的R=rP， 将(ID,-,x,c)插入列表Lrec而不是(ID,r,x,c).

3) 在猜测阶段， F输出V′-(xB+kz)T*=zβP作为CDH问题的回答.

4.2 不可伪造性分析

定理3A1类敌手的不可伪造性.

证明假设算法F以二元组(P,uP)为DL问题的挑战实例， 以Type-I敌手A1为挑战者， F的目标是计算u. 游戏开始后， F维护列表L1,L2,L3,LD,LSK,LPK,LS,LU分别跟踪A1对预言机H1,H2,H3， 部分密钥生成， 私钥生成， 公钥生成， 签密和解签密的询问. 此外， F维护列表Lrec来记录挑战者身份信息. 各列表初始均为空.

1) 系统建立

F运行Setup算法， 并发送系统参数params=(G,q,P,y,H1,H2,H3)给敌手A1. F设定y=up， 其他设置与定理1对A1的设置相同.

2) 查询阶段

与定理1相同， 敌手A1可执行多项式有界次的询问.

3) 伪造阶段

A1以IDA为发送者，IDB为接收者， 经过多项式有界次询问后， 输出消息m的一个伪造密文δ*=(s*,c*,T*).

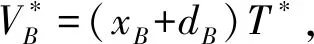
T*=βP=(s1(h+dA+xA)-xA)P=

(s2(h′+dA+xA)-xA)P.

所以有

s1(h+dA+xA)=s2(h′+dA+xA).

对A1敌手来说， 下面等式成立

s1(h+rA+uk+xA)=s2(h′+rA+uk+xA),

其中，k=h1=H1(IDA,RA)， 在此等式中只有u是未知变量， 所以u可以被计算出.

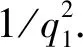
定理4A2类敌手的不可伪造性.

证明该定理的证明思路和方法与定理3类似， 重复部分不再赘述， 主要不同如下：

1) 在系统建立阶段， F为敌手A2设置y=zp， 其他设置与定理2对A2的设置相同. 敌手A2可以任意替换用户公钥.

2) 在伪造阶段， F根据分裂引理生成两个合法签名信息后， 敌手A2验证等式s1(h+rA+zk+xA)=s2(h′+rA+zk+xA)， 其中，k=h1=H1(IDA,RA). 在此等式中只有rA是未知量， 所以rA可以被计算出. 而在公钥生成询问中， F设置了R=rAP=uP， 所以u也可以被计算出.

4.3 性能分析

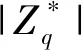
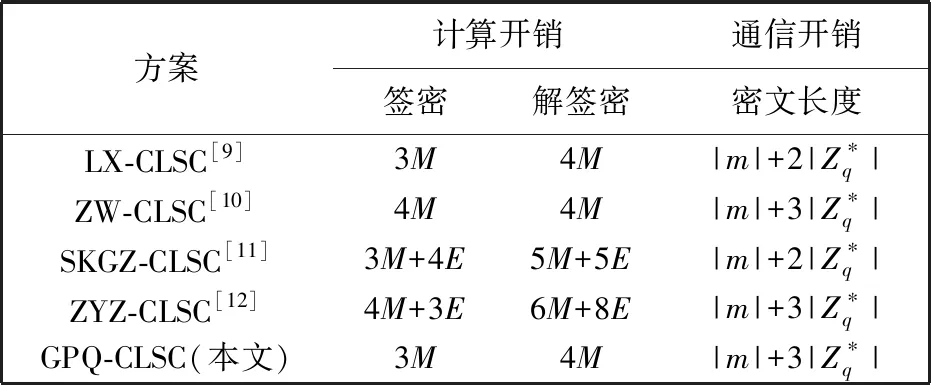
表 1 CLSC同类方案效率对比Tab.1 CLSC similar scheme efficiency comparison

方案的安全属性主要关注机密性和不可伪造性. 表 2 是GPQ-CLSC方案与其他几个同类方案的安全属性对比， 其中“√”表示具有该安全属性， “×”表示不具有该安全属性.

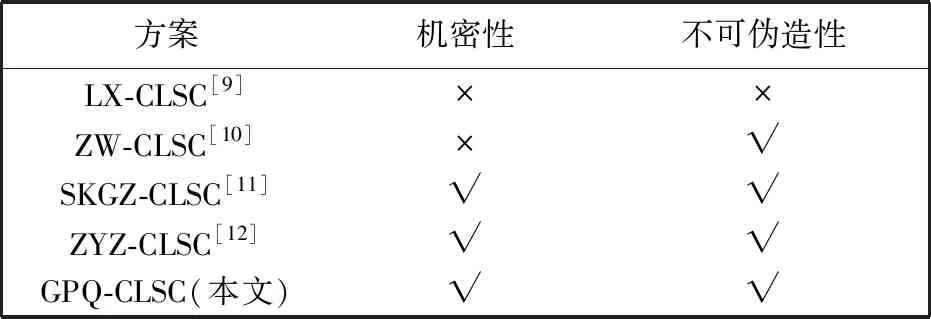
表 2 CLSC同类方案安全属性对比Tab.2 CLSC similar scheme security attribute comparison

5 结 论

签密作为数据信息安全保护的方法， 消息的保密性由加密来完成， 认证性由签名来实现， 在一个逻辑步骤内同时完成签名和加密， 具有较低的计算开销和通信开销. 本文对ZW-CLSC方案进行分析， 发现ZW-CLSC方案不满足正确性. 同时， 构造具体的攻击实例证明ZW-CLSC方案对A1类敌手不满足不可伪造性. 在借鉴ZW-CLSC优点的基础上， 提出GPQ-CLSC方案. 在随机预言模型中基于CDH假设和DL假设证明了GPQ-CLSC方案满足机密性和不可伪造性. 性能分析表明， GPQ-CLSC在保证安全性的前提下， 计算开销有所降低. 无双线性对运算的CLSC方案， 减少了椭圆曲线对运算的开销， 将更适用于无线传感器网络、 移动医疗数字网络、 无线体域网等终端资源有限的应用场景中.