基于改进的水平集模型工业零件图像分割方法

侯木舟， 陈英皞

(中南大学 数学与统计学院， 湖南 长沙 410083)

0 引 言

图像分割技术在机器人定位、 导航、 图像压缩以及目标检测等领域具有非常重要的意义[1-3]. 基于活动轮廓模型的改进的图像分割算法在算法中引入边界信息， 使算法形式多样， 结构灵活. 在活动轮廓模型的基础上发展得到基于水平集方法的图像分割方法， 将低维曲线嵌入高一维空间中， 并将曲线嵌入的位置作为零水平集的位置， 用连续曲线表示目标物体的边缘， 根据闭合曲线演化理论得到曲线的演化方程， 通过求解方程的能量范函最小值驱动曲线演化.在图像分割时， 最终零水平集截面的位置就是图像分割的边缘.

传统的边缘检测方法先检测图像中的边缘点， 接着将边缘点连接成闭合曲线， 构成图像的分隔区域， 常用边缘检测算子来检查图像中灰度、 颜色或纹理中不连续的部分， 常用的边缘检测算子有非微分算子如Canny算子， 一阶微分算子如Sobel算子， Robot算子、 Prewitt算子及二阶微分算子Laplacian算子、 Log算子等[4-6]. 但是几种边缘检测算子运算速度慢， 精度较低且轮廓过于粗糙.1987年Kass等人提出了活动轮廓方法[7-8]， 利用图像自身几何特征和图像数据的共同驱动以最小化能量函数的形式向边界运动. 但这个模型是基于能量泛函的优化问题， 容易陷入局部极小值[9]， 对于初始轮廓的选择过于依赖. C-V模型是基于图像中的区域分割的水平集模型[10]， Chan-Vese模型利用能量泛函最小值驱动曲线演化求解图像分割的结果. 但C-V模型需要不断初始化， 使计算量大大提高， 演化速率较慢[11-12].

在图像分割中， 当图像像素较小或者物体边界较为模糊时， 传统的水平集方法难以快速且准确地分割出图像中目标物体的轮廓， 本文通过重新定义δε(x)和Hε(x)函数， 改进了距离正则化水平集方法， 提高了图像分割的精度与速度.

1 改进的距离正则化水平集方法

设由y=f(x)表示平面上的曲线， 或隐函数形式y-f(x)=0， 表示x与y的对应关系

φ(x,y)=y-f(x)=0.

(1)

给定的一个初始封闭曲线C， 这条曲线可以沿着其法线方向向内或向外演化， 加入时间变量t后形成随时间变化的曲线簇C(t)， 我们将曲线簇C(t)看作高维空间上的一个曲面φ的零水平集合{φ=0,t},其中水平集是水平面上函数φ(x,y,t)值相同的点的集合， 零水平集就是所有函数φ(x,y,t)=0的点的集合，φ(x,y,t)是随时间变化的水平集函数.

对给定的水平集函数φ(C,t)， 则φ(C(t),t)=0是t时刻曲线C(t)的零水平集， 对φ(C(t),t)=0关于时间t求偏导数有

(2)

由微分几何中平面曲线的性质可知， 初始轮廓曲线的单位法向量N满足

(3)

曲线的演化方程为

(4)

式中：F是法向速度函数.

将式(3)， 式(4)代入式(2)中化简得到水平集基本演化方程

(5)

水平集方法的本质是求解关于时间变量t的一阶非线性偏微分方程式(5)， 这个演化方程属于哈密顿-雅可比方程， 可按照对时间分量Δt与空间变量分离求解的方法进行数值计算.

在水平集演化前， 先将水平集方程初始化为符号距离函数.在t=0时刻的水平集函数

φ(x,y,t=0)=sgn(x,y,C(t=0))×

dist(x,y,C(t=0)),

(6)

式中： sgn(x,y,C)是符号函数， 当点(x,y)在曲线C外部时， sgn(x,y,C)=1; 当点(x,y)在曲线C内部时， sgn(x,y,C)=-1. dist(x,y,C)是点(x,y)到曲线C的最近距离. 在建立符号距离函数的过程中分为两个步骤： 首先确定计算时点(x,y)在演化曲线的外部还是内部； 接着计算点到曲线C的最短距离.在曲线演化中保持|φ|=1， 以保证在数值求解中的离散网格大小为1， 使模型在数值计算中保持较高精度.

在曲线基于水平集方法演化过程中， 由于水平集方程的演化不是规则化的， 随着演化的进行会产生数值误差， 进而破坏了水平集演化的稳定性.为使得曲线在演化过程中的稳定性， 需定时将零水平集初始化为符号距离函数.常用的标准算法是求解以下哈密顿-雅可比演化方程直到一个稳定状态

(7)

零水平集的定时重新初始化步骤虽然保证了曲线在演化过程中的准确性， 但大大增加了计算量， 降低了模型的运算效率. Li等人提出了距离正则化水平集模型(DRLSE)[12]. 在这个模型中在基于边缘的水平集能量函数中增加了一项距离规则项作为惩罚项， 使得水平集函数能够自我约束地作为符号距离函数， 并构造了距离正则化项， 与轮廓的外部能量一起驱动初始轮廓曲线向实际物体轮廓边缘演化[13]. 距离正则化能量泛函可以定义为

E(φ)=μRp(φ)+Eext(φ),

(8)

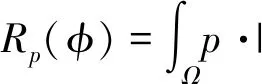
(9)

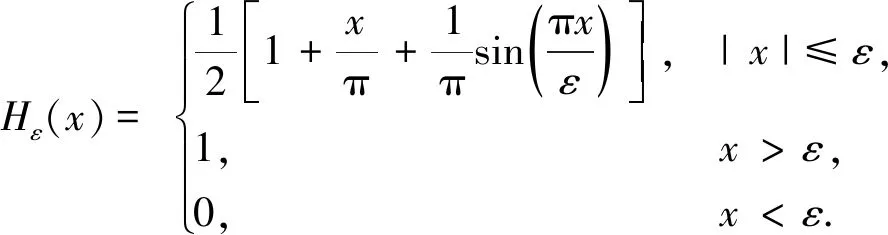
(10)

由于文献[8]将δ∈与Hε(x)定义为分段函数， 降低了模型的运算速度， 本文将δ∈与Hε(x)定义为连续函数的形式

(11)

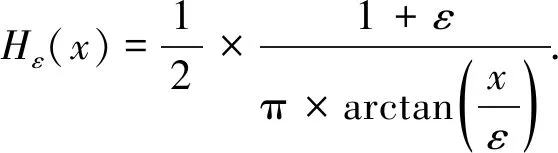
(12)

模型通过最小化能量函数E(φ)=μRp(φ)+Eext(φ)求解图像分割的边界， 为保持模型求解的稳定性， 需要合理地选取Rp(φ)的能量密度函度函数p(s)， 使水平集函数φ保持符号距离函数的性质， 即|φ|=1.

记s=|那么

(13)

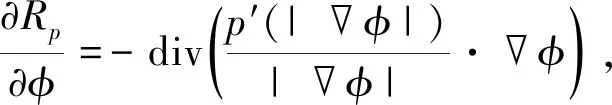
(14)

式中： div是散度.

接着通过寻找如下梯度下降流方程的稳定解使能量函数E(φ)最小化.

(15)

其中， 负号表示水平集函数φ(x,y,t)的方向与距离正则化能量泛函E(φ)的偏导数方向相反， 是能量函数E(φ)的最陡梯度下降流.

对式(8)计算偏导数并结合式(13)～(15)有

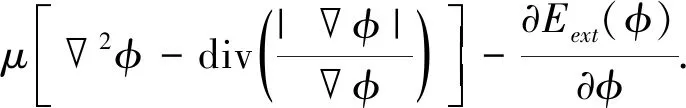
(16)

式(16)即为距离正则化演化方程.

结合图像轮廓的外部能量泛函的定义， 距离正则化演化方程式(16)可写为

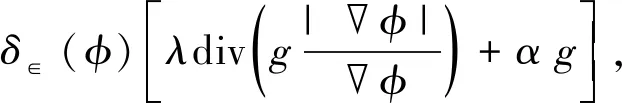
(17)

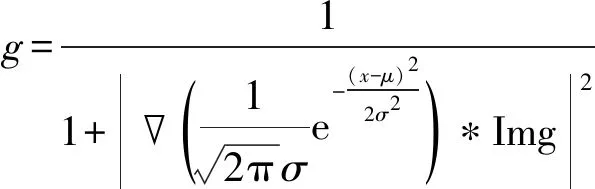
2 模拟实验

选取如下1 024×680的灰度图像作为测试图像， 如图 1 所示.

图 1 测试图像Fig.1 Test image

首先使用传统的边缘检测算法利用非微分算子Canny算子和一阶微分算子Sobel算子来检测图像的边缘轮廓， 边缘检测算子与边缘检测图像如表 1 和图 2 所示.

表 1 边缘检测算子及其边缘检测图像Tab.1 Edge detection operator and its edge detection image

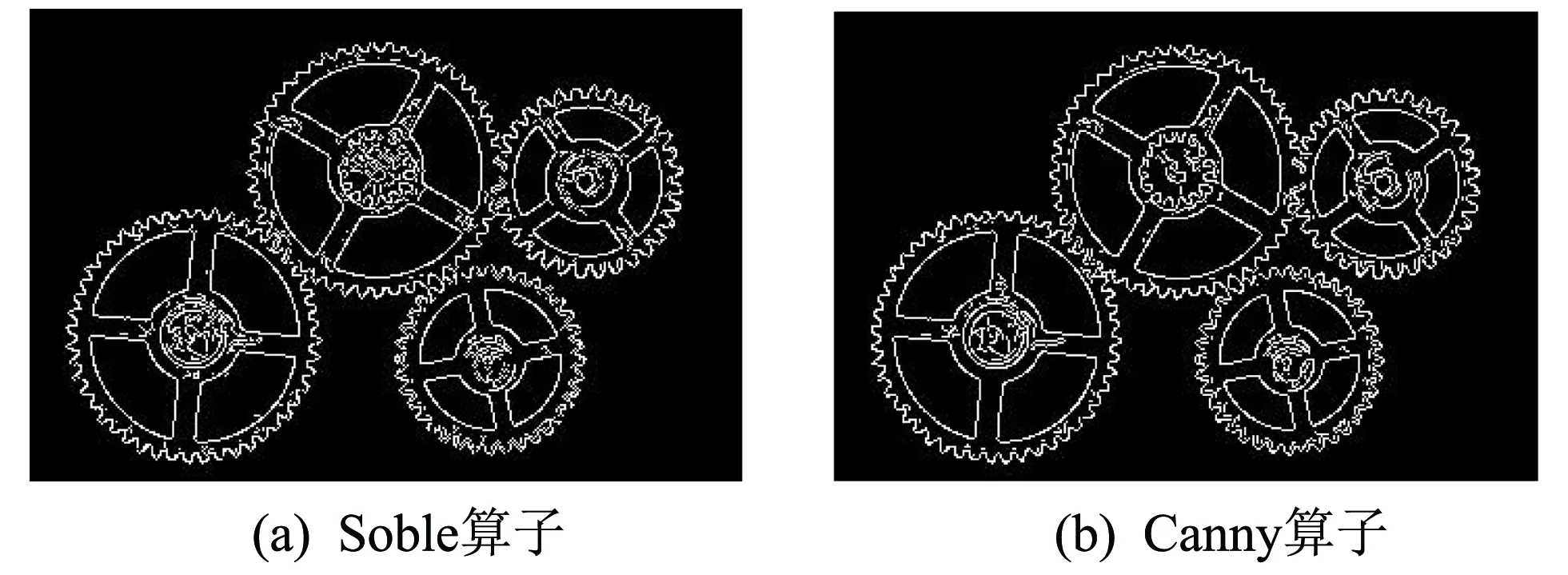
图 2 使用两种不同的边缘检测算子检测的零件轮廓Fig.2 Part contours detected by two different edge detection operators

通过实验发现， 使用几种边缘检测算子寻找图像中目标物体边缘运算速度慢， 精度较低且轮廓过于粗糙， 不能很好地将目标物体的边缘从图像中分离出来.

首先使用传统方法定义的δ∈与Hε(x)函数寻找目标物体的边缘轮廓. 选取图像中心为圆心， 图像宽度的2/3为半径的圆作为初始轮廓曲线进行演化.

图 3 使用传统方法定义的δ∈与Hε(x)函数时不同演化次数得到的轮廓曲线Fig.3 Contour curve obtained with different evolution times using the δ∈ and Hε(x) functions defined by the traditional method

图 4 使用传统方法定义的δ∈与Hε(x)函数时演化200次得到的轮廓曲线Fig.4 Contour curve obtained by evolving 200 times using the δ∈ and Hε(x) functions defined by the traditional method

由图 3 发现， 使用传统方法定义的δ∈与Hε(x)函数定义的水平集方程运算速度较慢， 在80次演化后无法得到目标图像的轮廓. 如图 4 所示， 让曲线继续演化， 经过200次演化， 该水平集模型依旧无法完全分割出目标图像的边缘， 耗时超过26s， 速度过慢无法满足实际应用中的使用需求.

为加快轮廓曲线的演化速度， 我们将目标图像压缩至原来的1/16， 及将图像的长和宽均缩小为原始图像的1/4， 得到256×170的灰度图像， 将压缩后的图像作为测试图像重新寻找目标物体的边缘轮廓曲线.

图 5 使用压缩后图像不同演化次数得到的轮廓曲线Fig.5 Contour curve obtained using different evolution times of compressed images

如图 5 所示， 即使使用了压缩后的图像， 在80次演化后依然无法得到目标物体的轮廓曲线， 但对比使用压缩前的图像， 轮廓曲线的演化速度大大提高. 如图 6 所示， 让水平集模型继续演化， 在200次演化后， 曲线内的面积变化小于2%， 可以认为曲线已经演化至目标物体轮廓上. 但由于使用的是压缩过的图像， 图像精度大大降低， 当对目标物体的轮廓精度要求较高时， 传统的距离正则化水平集方法不能快速而准确地寻找到目标物体的边缘轮廓. 本文对传统水平集方法中的δ∈与Hε(x)函数进行改进， 使其能更快速且准确地得到目标物体的边缘轮廓.

继续使用图 1 中的1 024×680的灰度图像作为测试图像.

图 6 使用压缩后图像演化200次得到的轮廓曲线Fig.6 Contour curve obtained by using image compression 200 times after compression

图 7 使用本文改进的δ∈与Hε(x)函数后不同演化次数得到的轮廓曲线Fig.7 Contour curve obtained with different evolution times after using the improved δ∈ and Hε(x) functions in this paper

如图 7 所示， 使用本文改进的δ∈与Hε(x)函数后， 曲线的演化速度大大提高， 且得到的轮廓相较于使用边缘检测算子得到的轮廓更加精确， 轮廓边缘更光滑. 初始轮廓曲线演化了80次后曲线内的面积变化小于2%， 得到了目标物体的轮廓曲线如图 8所示.

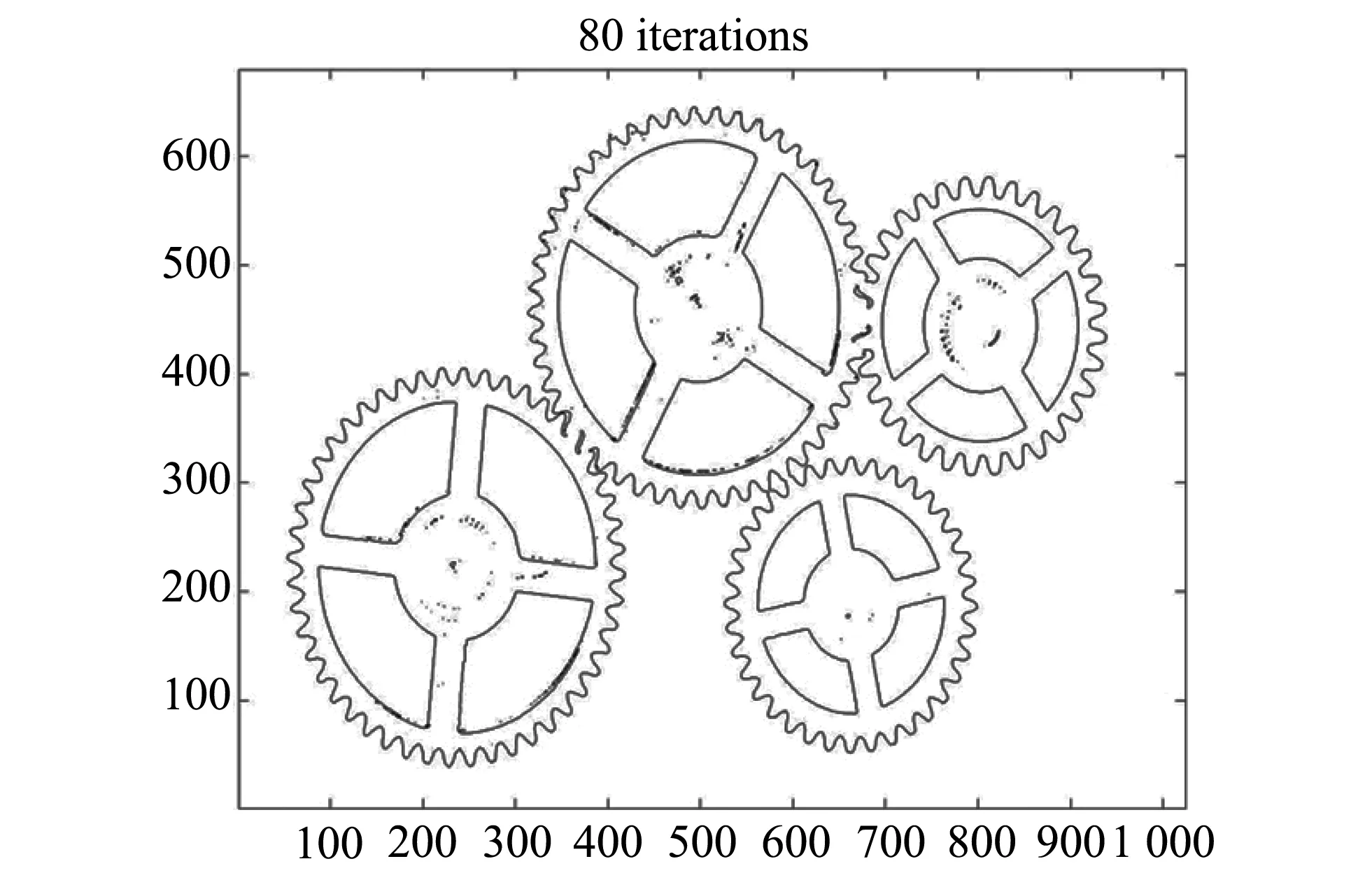
图 8 使用本文改进的δ∈与Hε(x)函数后得到的目标物体的轮廓曲线Fig.8 The contour of the target object obtained using the improved δ∈ and Hε(x) functions in this paper

即使我们对目标物体的轮廓精度要求较低时， 本文的方法相较于文献运算速度更快， 在使用压缩后的图像寻找目标物体边缘时， 本文的方法仅使用7次演化就得到了目标物体的边缘， 如图 9 所示. 不同方法的曲线深化时间对比如表 2 所示.

图 9 使用本文改进的δ∈与Hε(x)函数和压缩后图像得到的目标物体的轮廓曲线Fig.9 Contour curve of the target object obtained using the improved δ∈ and Hε(x) functions and the compressed image

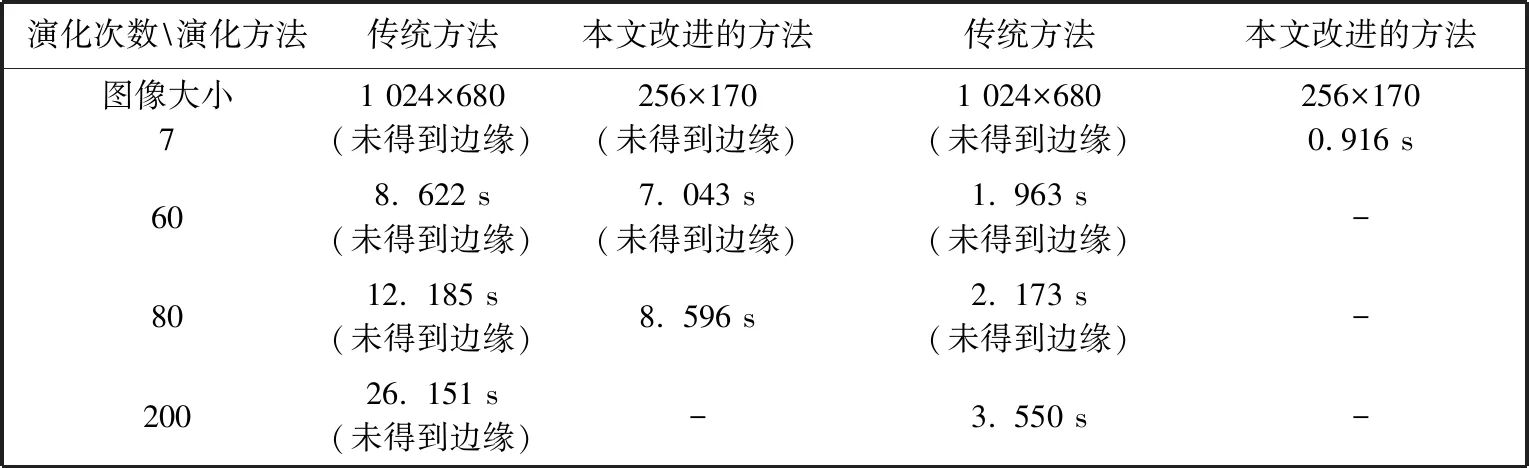
表 2 不同方法的曲线演化时间对比

3 结 论

对图像中目标物体轮廓的提取， 可以提高工业机器人的智能化水平， 可以让其自主地对目标物体进行定位与识别. 本文通过重新定义距离正则化水平集方法的函数， 提高了轮廓曲线演化的速率. 实验表明， 通过对传统的距离正则化水平集方法进行改进， 将寻找目标物体的轮廓时间缩短至原来的1/3， 大大提高了模型的运算速度， 扩大了模型的适用领域.