运载火箭推进剂复杂流动传热问题数值模拟中的模型简化方法

，,，，

(1.中国科学院国家空间科学中心, 北京 100190；2.中国科学院大学, 北京 100190；3.北京宇航系统工程研究所，北京 100076)

0 引言

在运载火箭动力系统总体设计中，越来越多地采用数值模拟方法。通过数值模拟，不仅可以对动力系统设计参数进行优化，还可以与理论设计、试验测量进行交叉对比验证，提高系统的可靠性[1]。由于运载火箭中的流动传热属于经典的流体力学和传热问题，相关的数值计算方法比较成熟，采用现成的商业软件，就可以进行计算，因而得到广泛使用。工程型号设计人员采用数值模拟方法，解决了大量动力系统设计中的问题[2-4]。

但是，在运载火箭改进优化或者是新型运载火箭设计过程中，往往会遇到各种复杂的流动与传热问题。直接建立的数值计算模型过于复杂，多种不同材料和结构耦合，同时出现在需要解决的问题之中。经常出现计算时间太长(数年)、收敛困难、程序调试困难等问题。此时对数值计算模型进行简化，缩短计算时间的同时，保证结果的正确性、实用性，就是一个关键问题。美国Space X公司的Falcon 1火箭在初始的3次试射中均失败，教训惨重。从公布的资料分析，Falcon 1号在设计上的经验教训之一是流体管理方面，推进剂贮箱没有安装防晃挡板。这可能是前两次发射失败的主要原因。之所以不安装防晃挡板，是由于该公司数值模拟研究结果表明没有必要安装[1]。发射失败后，他们找到了计算给出错误结果的原因是没有考虑分离过程中的干扰，数值计算的初始条件设置错误。从第3次发射开始，增加了贮箱防晃挡板，克服了推进剂晃动问题。由此可见，推进剂晃动的数值模拟工作需要相关研究经验作为基础，模型简化需要慎重。否则的话，很可能数值模拟得到与事实相反的错误结论，引起重大的设计错误。

早期的贮箱自生增压设计，都采用集总参数法，大大简化了计算。但缺点也十分明显，这种方法精度非常低，也无法预测飞行过程中具体的压力变化过程[5]。Ariane 5火箭上面级滑行期间压力计算和流动计算分别进行，使用了不同的计算模型[6]。其中，压力变化采用集总参数法进行计算，推进剂分布状态和流动则使用FLOW3D计算。这种简化方法避开了计算量大的难点，但是压力计算精度不够，也无法应用到更加复杂、要求更高的场合。

针对初始条件复杂、飞行过程复杂、边界条件复杂3类具体问题，结合我们十几年的研究经验[7-8]，介绍3种相应的模型简化方法——工程经验法、极限参数法、低维近似法，为推进剂复杂流动与传热的数值模拟提供参考。具体的数值模拟计算方法，可以参考Kassemi等[9]的研究。

1 工程经验法

液体火箭在飞行过程中，上面级可能关闭主发动机作空间惯性飞行(简称微重力滑行)，一段时间之后主发动机二次启动。通过微重力滑行，可以提高运载能力。为了保证主发动机二次启动成功，一般在微重力滑行期间使用较小的沉底发动机工作，让液体推进剂始终保持在沉底位置[1]。我国的空间探测工程要求优化微重力滑行段工作状况,即延长微重力滑行时间，同时尽可能减小沉底发动机推进剂用量。

针对微重力滑行后主发动机二次启动问题，需要通过数值模拟计算微重力滑行期间液体推进剂在贮箱中的分布、气液界面的运动情况。

推进剂流动状态高度依赖于初始条件。飞行过程中运载火箭的振动、姿态控制干扰、主发动机瞬间的关机过程都会影响该时刻的流动状态，该初始流动状态的选择和设置就成为一个关键问题。由于这些因素具有很强的不确定性，而且依赖于具体的工程型号，根据工程经验选择计算的初始条件是一个好的选择。参考工程遥测数据和Berglund等[1]的研究，在某火箭的设计过程中，选用侧向干扰力主推力10%大小作为初始干扰简化计算条件。计算得到推进剂晃动幅值为贮箱半径10%的初始干扰运动，作为微重力滑行期间流动计算的初始条件。

如图1所示，初始干扰在轴向过载作用下形成近似一阶晃动，晃动幅值为0.15m(最高点和最低点落差为两倍幅值，即0.30m，贮箱直径为3m)，t1时刻液体大部分区域速度接近于0，即流体近似处于动能极小，势能极大的状态。其左右两侧自由面附近液体位于极低和极高位置，t1时刻即最大势能时刻。在t2时刻，自由面附近液体竖直方向速度分量达到最大值，而且它们分别位于箱体左右两侧。此时波动的幅值最小，但动能最大；这时刻如果主发动机关机，在惯性作用下将于下一时段形成最大晃幅的波动，t2时刻为最大动能时刻。

(a) t1 (b) t2

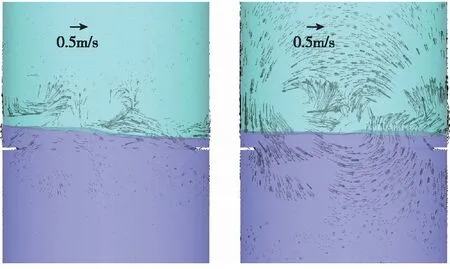
(c) t3 (d) t4图1 液氢贮箱主发动机关机前液面附近的晃动干扰简化，时间t1、t2、t3、t4分别是一个晃动周期内的4个不同时刻(深色为液氢，浅色为增压气体，矢量表示中心截面上流体的速度)Fig.1 Simplification of sloshing near the interface, in the hydrogen tank, before main engine cut-off, t1,t2,t3, and t4 are four separate moments in a sloshing cycle

通过工程经验法，快速得到了后续计算所需要的初始条件，省去了上面级火箭一次飞行段的直接三维非定常数值模拟计算。通常情况下，省去的部分采用10个CPU核计算，需要计算1m左右。

2 极限参数(状态)法

如前所述，主发动机关机过程也给推进剂流动带来了不确定性和复杂性。发动机关机过程中，1s～2s内，上面级过载从几个g快速过渡到10-3g的微重力状态。进入微重力时刻的流动状态是未知的，可以是前面所述晃动周期中的任意时刻，具有不确定性。此时，可以用极限参数(状态)法进行简化，分别有最大动能关机、最大势能关机两种极限状态。在保证主发动二次启动成功问题中，最大势能关机为最危险工况。此时推进剂在微重力滑行中运动最为剧烈，沉底困难。选用最大势能时刻作为开始微重力滑行数值模拟计算的初始时刻进行简化，满足主发动二次启动设计要求。

尽管如此，由于微重力滑行期间流动的复杂性，工程中通常需要进行保守设计，此时可以按照可能的最危险状态，进行沉底方案设计。假设经过长时间微重力滑行后，推进剂全部位于贮箱顶部，如图2所示，然后施加沉底力作用。通过三维非定常直接数值模拟，得到保守的沉底力大小和沉底时间。

图2 液氢贮箱推进剂沉底前的极限状态，液氢全部位于贮箱顶部Fig.2 Extreme status of the hydrogen propellant in the tank, liquid hydrogen all occupying the upper side of the propellant tank

3 低维近似法

上面级液氢贮箱在微重力滑行期间，在多种因素联合作用下，贮箱压力逐渐下降。引起贮箱压力下降的因素包括气枕温度/密度重新分层，气液界面传热、相变，贮箱壁面传热。由于推进剂干扰流动、非对称壁面传热、非轴对称调姿干扰的存在，贮箱压力对这些因素都很敏感，只能进行三维非定常直接数值模拟计算，才能够获得准确的压力下降预测，从而指导增压输送系统的优化设计。

最直接的三维非定常数值计算模型，几何模型上包括推进剂、金属贮箱、贮箱外表面的泡沫隔热层，时间上从上面级发动机一次工作段开始计算数百秒，然后主发动机关机，进入微重力滑行段。上述完整的几何和时间模型会遇到多方面的困难。1)几何模型复杂，推进剂、金属贮箱、泡沫分别是m、mm、cm 这3个尺度，网格数量大，网格质量差，程序很难收敛。2)即使程序收敛，计算时间也会很长，预计比只考虑推进剂建模、只计算微重力滑行期间的简化模型长10倍。如果采用10个CPU核计算，需要计算1a左右。这个时间对于运载火箭的任务适应性是很不利的。

采用只对推进剂建模，只计算微重力滑行期间的简化模型，可以大大节省计算资源。由此带来两个新的难点，一个是如何获得准确的初始温度分布，另一个是如何确定合适的热流边界条件。可以用低维度模型解决这两个难点。

首先，上面级主发动机一次工作段，流动主要是气枕区注入氢气，液氢从下面流出，气枕温度分布主要由氢气注入和推进剂液位下降共同决定，可以简化成轴对称流动与传热问题。因此，可以建立二维轴对称简化模型，初始条件由任务加注情况给定，快速计算得到主动飞行段末了时刻气枕的温度分布。然后以这个温度分布，作为微重力滑行段三维直接数值计算模型的初始条件，计算得到相应的压力下降过程。采用上述模型简化方法，计算得到的某飞行工况微重力滑行段开始时刻的气枕温度如图3所示。

图3 轴对称简化模型计算得到的某火箭液氢贮箱，微重力滑行开始时刻的温度分布(底部为液体推进剂，上部分为氢气)Fig.3 Temperature distribution in a launcher hydrogen propellant tank, at the beginning of microgravity flight, calcul-ated from an axial symmetry simplified model

贮箱和泡沫层的传热效应可以通过对流传热边界条件进行描述。为了获得较为准确的传热边界条件，与上面模型简化计算的方法类似，可以用低维近似法计算得到推进剂在贮箱壁面处的传热边界条件，单独对贮箱和绝热泡沫层进行建模。采用二维平板模型，分别对与载荷舱接触的顶部贮箱，内部与气枕接触、外部与地球或太空辐射换热的中上部贮箱等各部分贮箱单独计算，得到贮箱外表面泡沫平衡温度。然后假设泡沫温度沿贮箱厚度方向呈线性分布，计算得到热流密度，将该热流密度通过等效对流换热边界条件。

边界温度计算结果如图4所示，对与载荷仓接触的顶部贮箱，内侧采用气枕等温边界条件，外侧载荷舱300K辐射条件，计算得到泡沫外表面温度变化过程，最终平衡温度在270K附近。这样就得到了简化三维非定常计算模型所需要的热边界条件。

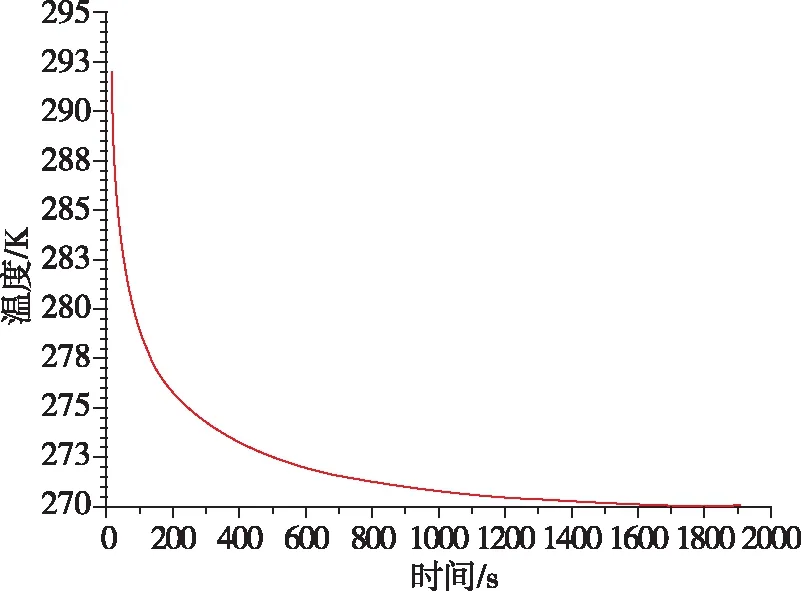
图4 二维平板简化模型计算得到的某火箭液氢贮箱在微重力滑行开始前的泡沫外表面温度变化Fig.4 Temperature variation at the outer side of the tank foam, before microgravity flight, calculated from a two-dimension simplified plane model

4 结论与讨论

结合运载火箭上面级微重力滑行期间的复杂流动和传热问题，总结了3种数值计算模型简化方法。这些模型简化方法可以加速数值模拟计算，同时，是否保持了工程型号设计需要的计算精度，需要与具体工程数据进行对比分析，进一步确认。

工程经验法适用于初始条件影响因素复杂，不确定因素多，直接数值模拟困难的情况。这时，通过火箭飞行数据和理论分析，结合工程人员的经验，给定一个合适的初始条件，不需要对长时间飞行进行数值计算，大幅减少了计算时间。

极限参数法应用于系统存在短时间的非线性变化，其变化过程(如主发动机关机等)复杂，变化的最后状态不确定的情况。通过分析该时刻状态的极限情况，设置相应的极限状态参数，进行保守设计计算，解决工程型号设计需求。

低维近似法适用于推进剂流动和传热，虽然复杂，但是具有对称性特征，可以通过低维模型简化，计算得到需要的初始条件和边界条件，大大简化核心计算模型。

必须指出，以上3种模型简化方法具有很强的经验性，运用时须十分慎重。理论计算科研人员需要加强和工程设计人员的讨论和沟通，尽可能对简化模型计算的结果与地面试验、相关飞行遥测数据进行比较验证，以保证简化模型的正确性。