拓扑优化结果的多视图参数化几何重构方法

2019-04-08胡三宝刘继鹏韩忠磊

数字制造科学 2019年1期

关键词：圆弧多边形视图

周涛，段薇，胡三宝，刘继鹏，韩忠磊

(1.武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉 430070；2.武汉理工大学汽车零部件技术湖北省协同创新中心，湖北武汉 430070；3.武汉船舶通信研究所，湖北武汉 430079)

拓扑优化在机械结构设计中应用越来越广泛，其数值计算大多基于有限元理论，得到的结果存在棋盘格现象、边缘呈明显锯齿状，不便后续处理，需要产品设计师以拓扑优化结果为参考，根据工艺和经验构造参数化模型，限制了拓扑优化的应用。

三维拓扑优化结果重构方法主要经历了等值面方法、曲面重构方法和参数化曲面重构方法3个阶段。

(1)等值面方法用等值面密度构造三角面片(或其他类型面片)并拼接成曲面，主要用于显示拓扑优化结果，存在锯齿状边缘，Lorensen等[1]提出的移动立方体等值面法(MC)应用广泛。

(2)曲面重构方法主要有网格平滑滤波和基于隐式函数的方法。等值面曲面仍有锯齿状，可用网格平滑法进行平滑，如拉普拉斯平滑[2]。隐式函数主要有泊松曲面和径向基函数。这两种方法主要用来显示曲面细节，加工成本较高。

(3)参数化曲面重构方法主要有基于特征分割和基于视图的曲面重构方式。

特征分割是通过实体的曲面信息或轮廓信息，将需要重构的实体分割出来进行拟合或调整[3-4]。基于视图的参数化曲面重构在拓扑优化结果重构中应用较多。在二维拓扑优化结果中，大多利用直线圆弧或几何模板对轮廓进行规整[5-6]。在基于切片视图的曲面重构中，陈思等[7]和Tang[8]采用NURBS和B样条曲面对切片数据进行重构，需要协调实体的复杂度和可加工性。在基于多视图的曲面重构中，William[9]和Shane[10]用形状模板逼近三维实体的二维轮廓，最后通过拉伸二维轮廓等操作重构曲面，重构曲面简单，但对组合图形的识别效果不好。

等值面方法和曲面重构方法主要用于优化结果的显示，没有考虑零件加工的工艺难度。参数化曲面重构考虑了曲面加工性，但采用B样条曲面、双四次曲面函数等方法构造的几何特征工艺成本较高。单视图方式只适合于二维的情况，对于三维结构由于不能识别曲面其他方向视图的几何信息，重构三维几何出现困难。

笔者采用多视图重构方法对拓扑优化结果进行重构。通过三视图、局部视图和坐标变换识别曲面任意点的坐标信息，结合考虑了加工工艺的整圆、椭圆和直线圆弧组合图形，重构出便于加工和几何建模的三维模型。可提高拓扑优化结果可加工性，节约工艺成本，便于尺寸/形状优化。

1 基于多视图构造三维参数模型

1.1 多视图构造3D参数化模型的数学基础

三维模型主要有线框模型、表面模型和实体模型，笔者采用实体模型描述实体全部的几何信息和拓扑关系。二维视图是三维实体在投影面投影生成封闭的轮廓线。其中三视图为同一坐标系下既相互独立、又相互关联的投影坐标系统。

三视图中的空间点可通过视图坐标获取。局部视图轮廓信息可通过坐标变换转化到三视图坐标系，有绕坐标轴旋转和平移变换，对三视图轮廓进行拉伸、旋转和布尔等操作生成实体[11]，如图1所示。实体的盲孔轴线与x轴夹角为θ，图1(a)为对齐的三视图，取点a(xa,ya,za),b(xb,yb,zb),c(xc,yc,zc),d(xa,yd,zd)，主视图的斜盲孔为椭圆，主视图拉伸xa-xb得到实体c，同理得实体d和e，实体f=c∩d∩e。图1(b)为局部坐标系下局部视图对齐，取点e、f、g和h，同上得实体j。实体j变换到三视图坐标系下，如图1(g)所示，实体f减变换实体j得实体k。

图1 多视图到三维实体

1.2 方向视图的构造

方向视图描述的是结构的二维轮廓。首先要从拓扑优化结果(MC等值面)点云构造出二维轮廓。

根据优化结果确定三视图、局部视图和特定截面视图的投影平面，基于MC三角片产生均匀曲面点云，将全部或部分点云投影到投影平面，用Alpha Shape算法[12]识别二维轮廓。

以图2(a)为例，两正方体内孔分别为通孔和盲孔，孔的轴向沿x轴。采用正投影，正方体1取正视图平面x=0为投影面，全部点云投影到投影面，即令x=0。正方体2将坐标系沿x轴平移到盲孔底面，取此坐标系的正视图平面x=0为投影面，在投影坐标系下，取x>0的部分点云投影到投影面。平面点云和二维轮廓如图2(b)所示。

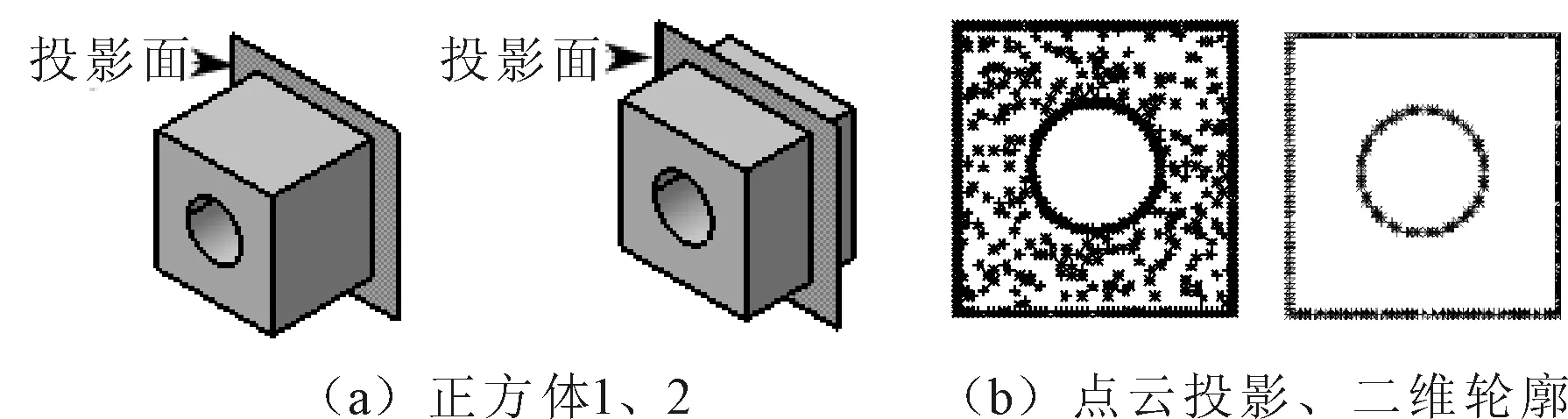
图2 有孔的正方体点云投影与二维轮廓识别

1.3 二维轮廓重构评价标准

将平面轮廓点列{Si=(xi,yi),i=1,2,…,N0}坐标转换为极坐标(ρi,θi)，极点/极轴为平均点/x轴。特征强度定为li=ρi/ρmax。以特征强度为y轴，点序列为x轴，绘制特征强度曲线，特征强度极大值点数目为特征点数目N(p)，若N(p)>1，找到相同数目的特征点T，T={Tj,1≤j≤N(p)}并据此将轮廓分段。每段轮廓点列采用直线和圆弧近似，并构造直线圆弧选择函数选择近似边，组合为多边形。其中特征点数N(p)等于近似多边形的顶点数p。其轮廓分段为：

Sg={Sg1,Sg2,…，SgN(p)}

Sgj={Si,Tj≤i≤Tj+1,

j=1,2,…,TN(p)-1}

SgN(p)={Si,i≥TN(p)||i≤T1}

(1)

若N(p)=1，采用整圆近似，若N(p)=2，分别用椭圆近似和分段近似两种方式，若N(p)>2，分段近似。多边形为整圆、椭圆和直线圆弧组合图形，但圆弧会增加多边形的复杂度，因此圆弧和直线的选取需要可控。

多边形近似评价标准压缩比、最大误差、灵敏值和误差平方和不能协调多边形顶点数最小化和近似误差最小化。根据张鸿宾等[13]的误差惩罚函数构造能控制直线和圆弧边选取的惩罚函数。

近似多边形中圆弧/直线边数为C(p)/L(p)。轮廓点Si到近似边的距离为该点的误差ei，轮廓分段误差e(Sgj)定义为属于该分段的点的误差平方和，采用圆弧/直线近似的轮廓分段误差为ec(Sgj)/el(Sgj), 其表达式如下：

ec(Sgj)/el(Sgj)=∑i∈Sgji(e2i)

(2)

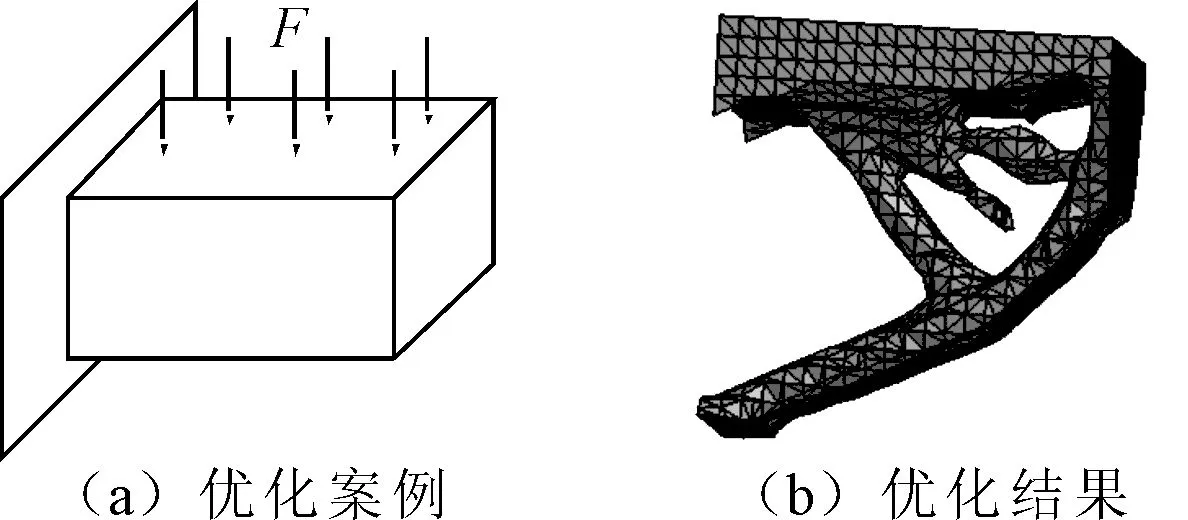
e(Sgj)=ec(Sgj)ec(Sgj)+eclf

el(Sgj)ec(Sgj)+eclf>el(Sgj)

(3)

eclf为轮廓分段选择因子，可以控制直线和圆弧的选取。近似多边形和轮廓点的误差e(p)定义为轮廓分段误差的和，即：

e(p)=∑N(p)j=1e(Sgj)分段近似

∑N0i=1(e2i)整圆椭圆

(4)

近似多边形与轮廓点的允许误差设为t，近似压缩比为m, 惩罚函数为P(e)，评价函数为J(p)。cf/lf是圆弧/直线边系数，其值越大，圆弧/直线边优先级越低。

m=N0N(p)N0<100

100N(p)N0>100

(5)

P(e)=exp((e-t)/m)-1exp(1)-1

(6)

J(p)=cf·C(p)+lf·L(p)+P(e(p))

(7)

式中：N0为点列数。

1.4 二维轮廓重构

(1) 内轮廓凹点和外轮廓处理。特征强度极大值作为特征点能识别凸点，不能识别凹点。拓扑优化结果的内轮廓整体呈现凸多边形，通过平滑即可滤去微弱凹点影响。明显凹点是优化不彻底部分，用下述算法删除，具体步骤如下：

Step1：简化轮廓曲线；

Step2：识别简化多边形凹点并删除；

Step3：简化多边形内外偏移2 mm(可调)，偏移环内的点为可处理的轮廓点。

去除外轮廓规整点，其余点形成独立的分割点列，分割点列和规整点列的特征点数和作为外轮廓的特征点数。

(2) 轮廓重构案例。二维轮廓重构流程为：

Step1：内轮廓凹点处理和外轮廓处理；轮廓点均匀线性插值，绘制特征强度曲线；

Step2：特征强度曲线多尺度平滑，取最大特征点数n，特征点数定为1～n。对每个特征点数找近似多边形；

Step3：对特征点数1～n，找最佳近似多边形，J(p)允许值为Jtol，若J(p)大于Jtol，返回Step2，增加特征点个数重新计算；

轮廓误差和噪声会干扰识别特征点，用多尺度移动平滑窗口平滑滤除。轮廓点列以0.08密度均匀线性插值，移动窗口大小为点数的0.02～0.20；cf和lf取1，eclf取1，Jtol取500，重构案例如图3所示。

获得轮廓最大特征点数10的特征强度曲线平滑滤波如图3(b)所示。其中整圆近似的J(p)值为330.124 2；特征点数为4时，J(p)最小，为4.404 9，小于Jtol。

图3 轮廓重构

1.5 轮廓后处理

邻边形式为直线和直线、直线和圆弧、圆弧和直线、圆弧和圆弧，用公切圆弧和公切线连接，C1连续。根据部件尺寸和加工工艺确定合适的倒圆角半径，制作公切圆弧半径表。直线和圆弧相离时公切圆弧半径要查表校正，其余的公切圆弧半径cr统一确定，近似圆弧半径为CR。

以直线圆弧相交为例说明确定公切圆过程，如图4所示，图4(a)黑点为特征点，白点为非特征点，虚线为近似圆、近似直线和辅助线。近似圆弧分段的轮廓点列的时针方向为近似圆弧方向WC。过渡圆弧的时针方向为过渡圆弧方向Wt。

图4 圆弧和直线过渡连接

两相邻边由3个特征点分割，依次为A1、A2、A3，其中A1、A2和圆心的连线与圆交于a1、a2，A3在直线的投影点为a3。直线与圆的交点为B1、B2，其中弧长B1A2

表1 部分邻边连接情况

2 算法实例

拓扑优化案例和优化结果如图5所示。

图5 重构实例

轮廓点插值密度取0.08，移动窗口大小为点数的0.02～0.20；cf和lf取1，eclf取1，Jtol为500。重构过程如图6所示，选yz视图和xz视图进行轮廓重构，如图6(a)和图6(b)所示，以yz视图和xz视图为基准，对称拉伸50 mm，得到图6(c)的实体，对齐布尔交，得到图6(d)的实体。xy视图对重构结果的影响不大，会显著增加曲面加工难度。