自动驾驶汽车横向跟踪控制方法研究

陈治莹,聂琳真,管家意

(武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070)

近年来，自动驾驶汽车成为社会广泛关注的对象。由于汽车系统复杂，运行工况多，自动驾驶汽车如何跟踪轨迹成为学术界研究的重难点。

自动驾驶轨迹跟踪控制主要分为纵向跟踪控制和横向跟踪控制。纵向控制指对汽车车速的控制，主要是对油门和刹车的控制[1]。横向控制主要是对方向盘的控制，使汽车行驶时处于期望轨迹上[2]。相较于纵向跟踪控制，由于安全性等问题，横向跟踪控制更为复杂和重要，对算法要求相对较高。笔者主要针对自动驾驶汽车轨迹跟踪中横向跟踪控制问题进行研究。

在横向跟踪控制研究中，Wu等[3]基于汽车动力学模型，设计状态反馈控制器，并利用模糊增益规划调节输入输出；Falcone等[4]利用模型预测控制(model predictive control,MPC)分别就汽车非线性模型和汽车时变线性模型设计了两类控制器，并给出仿真模型和实车实验结果； Choi等[5]基于视觉导航，考虑车辆的转向延迟和侧滑，以航向误差作为PI控制器输入，实车测试表明所建立的PI横向控制器具有较好的跟踪精度和乘客舒适性；Emirler等[6]设计了参数自调整的PID横向控制系统，并通过仿真验证表明，该控制器在环形道路和曲线道路均具有较好的横向跟踪效果。Hessburg等[7]设计了基于模糊规则的横向控制器，并在相同测试条件下对线性二次型以及PID横向控制方法进行对比，研究表明该模糊控制方法处理车辆动力学的非线性问题具有显著优势。Zhao等[8]针对车辆换道和车道保持的横向运动设计了多模型的模糊控制器MMFC(a multi-model fuzzy controller)，该多模型的模糊控制器包括4个车速区域的模糊控制器；Akca等[9]基于进化的Takagi-Sugeno模糊控制ETS(evolving takagi-sugeno)建立驾驶员模型实现自动驾驶汽车的纵横向综合控制；Rasterllia等[10]基于模糊逻辑开发了一种串联结构的横向控制器，在实车上对该控制器进行了不同车速的测试。

笔者主要研究车辆根据决策规划输出的期望轨迹和车辆当前姿态、位置、车速等信息计算方向盘转角，转化成控制信号，输出给执行机构控制车辆，以实现自动驾驶汽车平稳精准的跟踪期望轨迹。通过仿真分析总结纯追踪跟踪控制方法的特点和使用范围。

1 纯追踪模型搭建

1.1 纯追踪模型控制方法

纯追踪模型是一种基于几何的计算方法，其难点是确定合适的预瞄距离，以达到较优的跟踪效果。由于其算法简单、易于实现，在车辆跟踪控制中得到广泛应用。纯追踪横向跟踪控制模型结构原理如图1所示。

图1 纯追踪横向跟踪控制模型结构

如图1所示，该模型包括预瞄距离求解、坐标转换、纯追踪模型和车辆模型等部分。其中，根据当前车速vc求解出预瞄距离ld；由预瞄距离ld、车辆当前坐标(Xc,Yc)和期望轨迹点(X,Y)搜索出预瞄点(Xp,Yp)；通过坐标转换大地坐标系下的预瞄点(Xp,Yp)转换到车辆的局部坐标系xoy下，并求解出预瞄方向角η；纯追踪模型根据预瞄方向角η和预瞄距离ld求解出前轮转角δ。

1.2 纯追踪模型算法研究

车辆行驶时受到多个方向力的作用，但在车速较低或车辆做直线运动时，车辆受侧偏力较小，可以忽略不计，为简化模型，忽略轮胎受到的侧偏力。纯追踪轮胎转向模型如图2所示。

图2 纯追踪的转向几何学模型

在图2中，研究对象为汽车前轮转角δ与汽车预瞄点(xp,yp)。设车辆质心与预瞄点的曲率半径为R0，车辆转向半径为R，预瞄点和质心距离为ld，预瞄方向为角η。则关系式如下：

R=R0sinβ

R0=ld2cosθ

θ=180-(η+β)

(1)

1.3 纯追踪模型的坐标转换

以车辆坐标系为参考坐标系，通过坐标转换求解预瞄方向角η。其中规定预瞄方向角η以绕x轴逆时针旋转为正，反之为负；坐标转换后，得到预瞄方向角η。坐标转换如图3所示。

图3 坐标转换

坐标转换过程包括坐标平移和坐标旋转。坐标平移是将期望轨迹的预瞄点坐标系从大地坐标系XOY平移至车辆质心XtOtYt，平移之后的坐标与原始坐标之间的关系为：

Xtp,Ytp=(Xp-Xc,Yp-Yc)

(2)

通过旋转XtOtYt坐标系与车辆坐标系xoy重合，可将期望轨迹上预瞄点(Xtp,Ytp)转化至车辆坐标系中，旋转之后的坐标点(xp,yp)与平移之后的坐标点(Xtp,Ytp)之间的数学关系可表征如下：

xp

yp=cosψsinψ

-sinψcosψXtp

Ytp

(3)

式中：ψ为车辆航向角;(xp,yp)为坐标转换之后期望轨迹上预瞄点(Xp,Yp)在车辆坐标系中的坐标点。

2 横向跟踪控制模型仿真分析

为验证所构建横向跟踪模型的跟踪效果，利用CarSim和Simulink搭建汽车横向跟踪模型，并选取典型仿真工况对模型进行仿真验证。

2.1 仿真环境和仿真模型的搭建

2.1.1 构建仿真试验环境

如图4所示双移线存在直线道路和两个方向相反的紧急弯道，能较好验证汽车横向跟踪控制模型在直线、紧急弯道以及变曲率路况的跟踪特性。因此采用双移线试验路况作为典型的仿真验证路况，具体仿真试验路况参数，参照ISO/3888技术报告和GB6323-86标准。

图4中各参数值为：S0=50 m；S1=15 m；S2=30 m；S3=S4=25 m；S5=30 m；S6=50 m。变道距离D=3.5 m；标杆宽度B1=1.1b+0.25；B2=1.2b+0.25；B3=1.3b+0.25，其中b为车辆宽度。

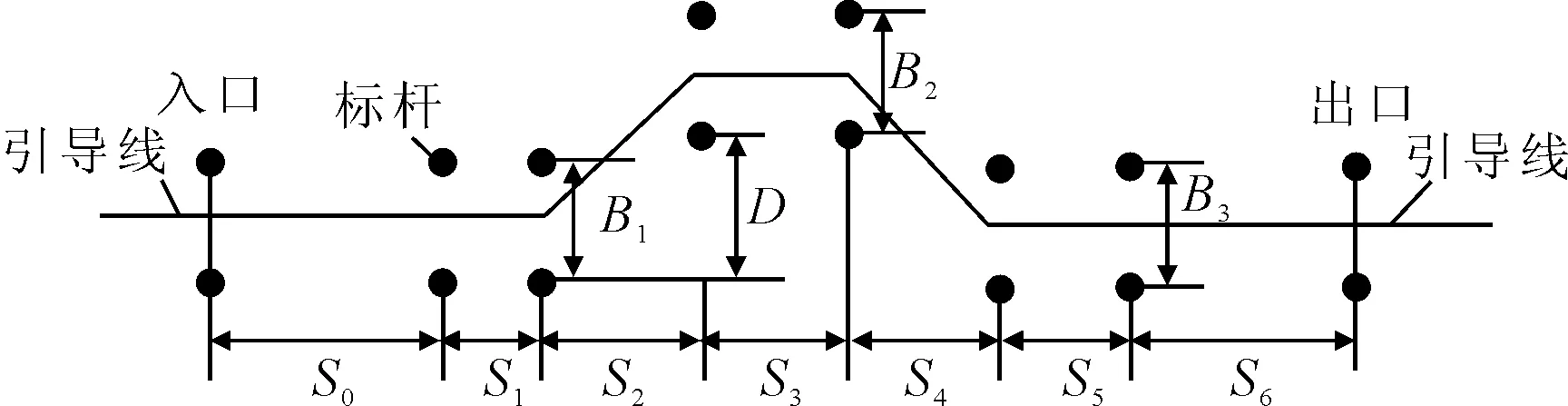
图4 双移线仿真道路轨迹示意图

根据相关标准，在CarSim中构建双移线仿真路况，并根据路径规划准则规划出期望轨迹。CarSim中的双移线仿真路况和期望轨迹曲线如图5所示。

图5 双移线仿真场景及轨迹曲线

2.1.2 仿真模型

根据上述所建立纯追踪跟踪控制模型，在CarSim中搭建仿真环境模型，在Simulink中搭建基于纯追踪的横向跟踪仿真模型。

图6为CarSim/Simulink联合仿真模型，图7为纯追踪横向跟踪控制模型。其中纯追踪横向跟踪控制器以车辆横纵坐标位置、车速和方位角作为输入，方向盘转角作为输出。

图6 CarSim/Simulink联合仿真模型

图7 纯追踪横向跟踪控制仿真模型

2.2 模型仿真分析

为分析纯追踪模型的跟踪效果，选取横向跟踪偏差、横摆角速度和侧向加速度作为评价指标。横向跟踪偏差反映了横向跟踪精度，横摆角速度和侧向加速度反映车辆平顺性好坏。

图8为纯追踪控制方法跟踪双移线的实际轨迹与期望轨迹，可以看出在直线道路上横向跟踪偏差较小，在急弯部分，跟踪偏差变大，且车速越快偏差越大。其中在高速工况下紧急弯道环境下，横向跟踪偏差较大。但都小于0.2 m，满足自动驾驶汽车横向控制安全性的需求。

图8 纯追踪模型跟踪双移线的实际轨迹与横向跟踪偏差

3 结论

针对无人驾驶横向控制问题，对纯追踪模型进行研究。选取双移线为跟踪轨迹，然后基于CarSim和Simulink进行联合仿真。仿真结果表明，该纯追踪模型在曲率较小、车速较低的工况下，跟踪精度高；在高速急弯工况下，跟踪偏差增大，但能满足自动驾驶汽车横向控制安全性的要求。