大规模多输入多输出系统中基于匹配博弈的导频分配算法

冯文江， 李 乐， 代才莉,2

(1. 重庆大学 通信工程学院， 重庆 400044； 2. 重庆电子工程职业学院 通信工程学院， 重庆 401331)

大规模多输入多输出(MIMO)系统在基站侧配置了大量可控天线单元，利用空间自由度(DoF)来提高能量效率和系统容量[1].基于随机矩阵论(RMT)的分析表明[2]，随着基站天线数趋于无穷大，小区内用户间的干扰和不相关噪声逐渐消失.而大规模MIMO技术依赖于发射机和接收机所获的信道状态信息(CSI)，通常采用基于导频的数据辅助技术来进行信道估计[3].由于正交导频资源有限，所以小区间导频复用产生的导频污染[4-5]将影响信道估计的精度，进而降低上行接收检测和下行预编码的性能.抑制导频污染的主要途径包括合理分配导频、设计信道估计算法、采用预编码[6-9].相关研究包括：文献[10-11]中提出一种相邻小区间异步传输的时移导频分配方法，能够有效抑制导频污染，但会导致数据与导频之间产生相互干扰；文献[12]中提出一种智能导频分配算法，可为信道质量最差的用户分配干扰最小的导频，以降低系统的导频污染；文献[6,13]中将小区划分为中心区和边缘区，使各小区的中心区用户复用相同导频，给边缘区用户分配正交导频，以牺牲中心区用户的部分性能为代价来减少导频规模；文献[14]中将时移与小区划分相结合，从时域和空域的角度来降低导频复用度和受干扰角度，从而降低了导频污染；文献[15]中提出基于用户到达角(AOA)的导频分配方案，但要求AOA的扩展很小，不符合实际；文献[16]中提出一种预编码方案，通过多小区联合处理的方法来减轻小区间的干扰，但由于信息交换的开销较大而造成频谱效率降低；文献[17]中提出一种基于空间分割的盲算法以抑制小区间的干扰，但其复杂度较高；文献[18]中针对大规模多输入多输出频分双工(MIMO FDD)系统的下行链路传输，提出一种综合优化导频训练时间、导频功率、数据功率的迭代能效资源分配算法，以使能量效率和频谱效率最大化；文献[19]中分析了导频长度对系统性能的影响，给出了大规模MIMO FDD系统中基站天线数增加时导频长度的选取准则.

本文根据匹配博弈论[20]的思想，提出基于匹配博弈的导频分配(PA-MG)算法，将导频分配过程抽象为用户与导频之间的博弈匹配.在用户侧，依据用户效用函数生成对导频的偏好列表，并向排列最优的导频发出申请；在基站侧，根据导频效用函数生成对用户的偏好列表，将对应的导频分配给列表中排列最优的用户，从导频分配的角度抑制用户间的干扰，降低用户间潜在的导频污染，使得上行链路中基站能够根据导频信号获得更加准确的信道估计，从而提升系统的上行链路可达速率.

1 系统模型

图1所示为一种简化的多小区多用户大规模MIMO系统模型，包括L个正六边形小区，每个小区中心配备一个基站，每个基站配置M根天线，且各天线之间不存在空间相关性，可同时为小区内多个用户提供服务，小区半径为R.假设每个小区随机均匀分布K(M≫K)个单天线用户，将位于小区j的用户k与小区i的基站天线之间的信道传播向量[6]模型化为

(1)

式中：g〈j,k〉,i为M×1维小尺度衰落向量，服从独立同分布，且服从均值为0、方差为IM的复高斯分布[6]，即g〈j,k〉,i～CN(0,IM)；β〈j,k〉,i为大尺度衰落系数，同一基站不同天线的β〈j,k〉,i相同，且与用户有关，具体表达式为

图1 系统模型Fig.1 System model

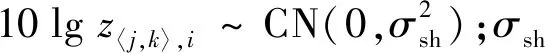
(2)

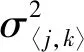
当M→∞时，式(2)可简化为

(3)

由此获得小区j中用户k的上行链路可达速率为

(4)

式中：μs为导频开销造成的频谱效率损耗；E[·]为数学期望.

2 基于匹配博弈的导频分配算法

将导频分配等效为最大化系统的上行链路可达速率，即

(5)

PA-MG算法包括两步，具体描述如下：

(1) 在用户侧，以各小区用户分配导频后接收的信干噪比作为用户效用函数，每个用户根据自身效用函数生成对导频的偏好列表，并向排列最优的导频发出分配申请；

(2) 在基站侧，以能够达到的上行链路可达速率作为导频效用函数，根据导频效用函数降序的排列生成对用户的偏好列表，并将对应的导频分配给列表中排列最优的用户.重复用户申请及导频分配过程，直到完成所有用户的导频分配.

需要说明的是，在执行PA-MG算法前，用户应向基站上传自身位置和导频发射功率等信息，以便在执行PA-MG算法过程中基站之间能够交换信息，从而协作完成导频分配.

2.1 用户效用函数

设计的用户效用函数如下：

(6)

由式(6)可见，当给用户〈j,k〉分配导频φi时，接收的信干噪比越高，用户的效用函数越大.

2.2 导频效用函数

设计的导频效用函数如下：

Uφi(〈j,k〉)=lb(1+U〈j,k〉(φi))+

(7)

式中：Ω(φi)为已分配导频φi的用户集合；O〈j′,k′〉={〈j″,k″〉:p〈j′,k′〉=p〈j″,k″〉}{〈j′,k′〉}，为除〈j′,k′〉之外使用相同导频的用户集合.

由此可见，导频效用函数包含两部分：第1部分是申请导频φi的用户可达速率；第2部分是假设给小区j的用户k分配导频φi后，系统中已分配导频φi的用户可达速率的总和.

2.3 算法流程

在描述算法流程之前，首先给出匹配矩阵M的定义和构造方法.M是一个L×K阶矩阵，其元素mjk=φi(j=1,2,…,L;k=1,2,…,K;i=1,2,…,S)表示给小区j的用户k分配导频φi.未分配导频时，M中元素的初始值为0.

PA-MG算法的流程如下：

(1) 初始化.选择由L个小区构成的蜂窝系统的中心小区，为该小区内所有用户随机分配正交导频序列，并将已分配导频的用户加入匹配矩阵M.

(2) 用户生成对导频的偏好列表.由用户效用函数(式(6))计算用户〈j,k〉对可用导频序列集合S的效用函数值，其中同一小区内的导频不复用，在可用导频序列集合中剔除小区j内已分配的导频序列；按照用户效用函数值降序的排列生成对可用导频序列的偏好列表

U〈j,k〉={φ1,φ2,…,φS} (j∈L,k∈K)

(3) 用户竞价.用户〈j,k〉向排列靠前的一组导频子集φi发出申请.

(4) 基站生成对用户的偏好列表.由导频效用函数(式(7))计算所有申请导频φi的效用函数值，并根据导频效用函数值降序的排列生成对请求用户的偏好列表

Uφi={〈j,k〉,…,〈m,n〉} (j,m∈L;k,n∈K)

其中，同一小区内的导频不复用，即若匹配矩阵M的小区j中存在用户已分配导频φi，则将导频φi和用户〈j,k〉从各自偏好列表中剔除.

(5) 基站决策(导频分配).根据U〈j,k〉和Uφi执行匹配博弈，将对应的导频序列分配给偏好列表中排列最优的用户，并将已分配导频的用户加入M中.

(6) 重复执行以上步骤(2)～(5)，更新用户效用函数及其偏好列表和导频效用函数及其偏好列表，直到完成所有用户的导频分配.

2.4 算法的收敛性分析

在多小区多用户大规模MIMO系统中，总的用户数L×K远大于导频数S，但因同一小区内的导频不复用，故导频数S应不小于单小区的用户数K，博弈是一对多匹配博弈，即一个导频匹配多个不同小区的用户.

(1) 当导频数等于单小区用户数时，算法结束的条件是已为所有用户分配导频.根据算法流程，由于未限制导频复用次数，意味着每个导频必然在每个小区复用，且所有导频的复用次数相同，即小区数均为L，最后形成了每个导频与每个小区用户两两匹配.

(2) 当导频数大于单小区用户数时，单小区内所有用户完成导频分配后还会剩余导频资源.根据算法流程，剩余的导频将根据分配原则分配到其他小区或复用.此时的某些导频复用次数将减少，但由于导频复用次数无限制，所以最终所有用户必然会完成导频匹配.

由此可见，PA-MG算法是收敛的.

此外，将本文的PA-MG算法与文献[4]中的CS(Classical Scheme)算法、文献[20]中基于潜博弈的导频分配(PG-PA)算法以及文献[21]中的WGC-PD(Weighted Graph Coloring Based Pilot Decontamination)算法相对比可见：CS算法随机分配导频，小区间无协作；PG-PA算法以最小化用户间的干扰为目标，采用潜博弈分配导频，能够降低导频污染，但仅适用于小区用户较少的场景，且复杂度高；WGC-PD算法引入用户间潜在的导频干扰参数，结合贪婪思想寻找潜在的干扰最小的用户并为其分配干扰最小的导频，以提高用户的最小信干噪比，但牺牲了潜在的导频干扰小的用户性能；而PA-MG算法以系统上行链路可达速率最大为目标分配导频，并均衡了用户能够达到的性能与分配导频后产生的干扰，既不会牺牲小区间干扰小的用户的性能，也兼顾了小区间干扰大的用户的性能.

特别地，本文从多小区多用户大规模MIMO系统整体的角度分配导频，相比于分区域导频分配，所涉及的问题更多.执行PA-MG算法时，假设小区用户随机分布且移动范围可控，但在实际中，小区用户位置移动过大时将可能发生小区切换，因此，本文采用定时监控来反馈用户位置信息，并结合用户的移动、分布来评估算法的性能.一旦超过某一阈值，则应重新执行PA-MG算法，并按需调整分配导频.但是，针对用户快速移动而导致小区间频繁切换的问题，采用PA-MG算法重新分配将使导频分配次数增加，从而导致算法的时间复杂度增大.

3 仿真结果与分析

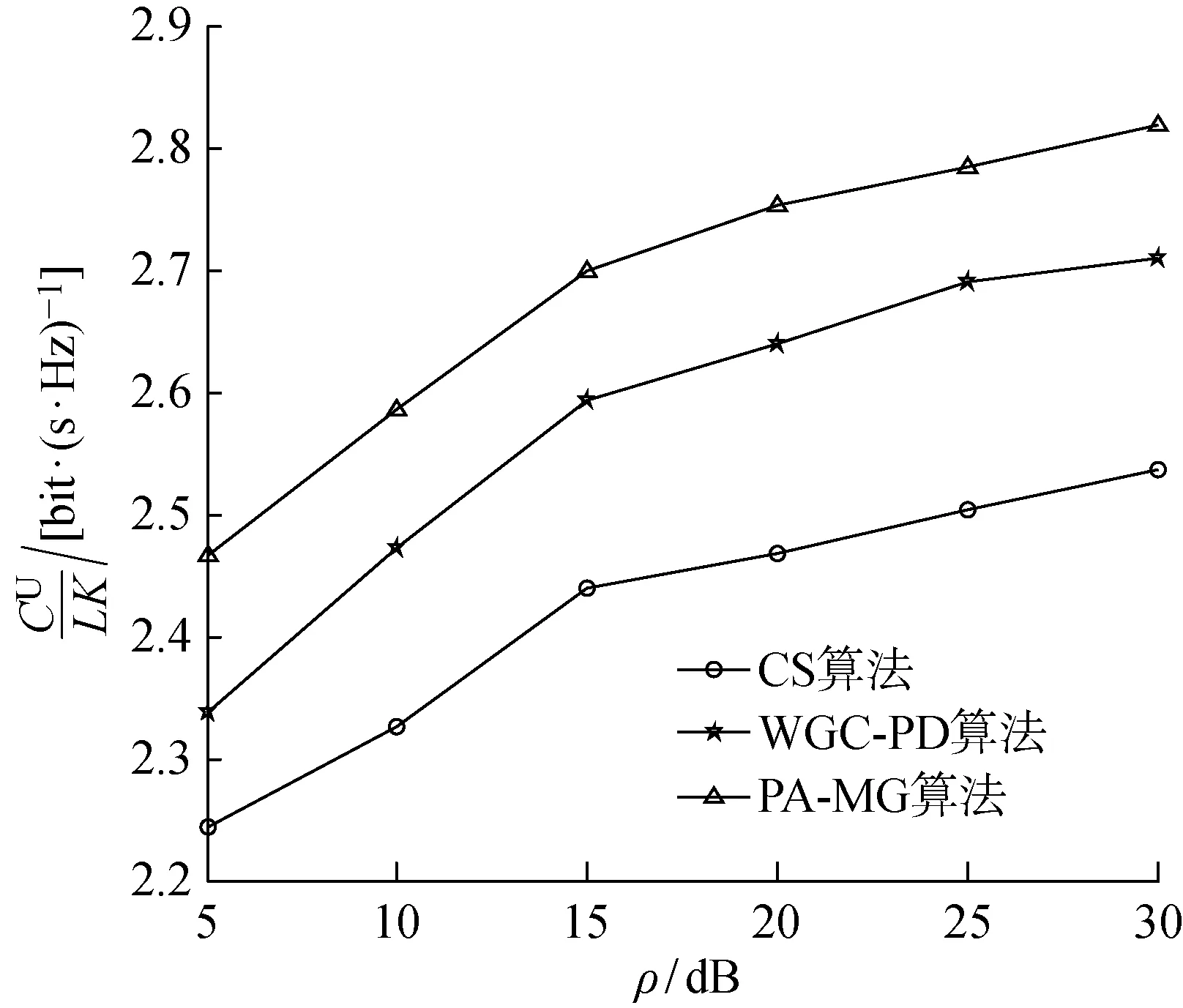
运用Monte Carlo仿真方法分析PA-MG算法的性能.利用图1中的多小区多用户大规模MIMO系统模型，各小区基站配备M(10

将PA-MG算法与CS算法、PG-PA算法和WGC-PD算法进行对比仿真，所得单小区用户数K=6,7时的上行链路用户平均可达速率CU/(LK)对比如图2所示，图3所示为4种算法的收敛时间随用户数变化的情况.综合图2和3可以看出：当小区用户较少时，采用PG-PA算法所得上行链路用户平均可达速率相对较高，但随着用户数增加，算法的收敛时间迅速增加，时间复杂度很高，无法适用较多用户数的应用场景；而PA-MG算法比WGC-PD算法的上行链路用户平均可达速率高，而收敛时间仅略有增大.

图2 上行链路用户平均可达速率Fig.2 Average uplink achievable rate per user

图3 算法收敛时间随用户数变化的情况Fig.3 The convergence time varies with the number of users

考虑到PG-PA算法的时间复杂度太高，在仿真较多用户时，本文选用CS算法、WGC-PD算法与PA-MG算法进行对比，图4所示为3种算法的上行链路用户平均可达速率随基站天线数变化的情况.由图可知，当基站天线数增加时，3种算法获得的上行链路用户平均可达速率都有所提高，这是因为随着基站天线数增加，热噪声和小尺度衰落效应逐渐消失.在同等条件下，PA-MG算法优于其余2种算法，获得了更大的上行链路用户平均可达速率，对导频污染的抑制效果显著.

图4 上行链路用户平均可达速率随基站天线数变化的情况Fig.4 Average uplink achievable rate varies with the base station antenna number

图5和6所示为M=512时上行链路用户信干噪比和上行链路可达速率的累积分布函数CDF的变化曲线.由图可知：PA-MG算法优于CS算法；相比于WGC-PD算法，虽然PA-MG算法的低SINR的用户相对较多，但高SINR的用户以及能够获得高可达速率的用户分布更多，总体而言，执行PA-MG算法时用户的SINR分布相对均匀，能够获得较高的上行链路用户平均可达速率.

图5 上行链路用户信干噪比的累积分布函数Fig.5 CDF of users’ uplink SINR

图6 上行链路用户可达速率的累积分布函数Fig.6 CDF of users’ uplink achievable rate

图7所示为上行链路用户平均可达速率随阴影衰落标准差σsh的变化情况.由图可知，随着σsh增大，3种算法的上行链路用户平均可达速率都有所降低，这是因为σsh的增大会导致大尺度衰落因子增加，进而影响SINR和用户可达速率.但由图7还可以看出，相比于其他2种算法，PA-MG算法的上行链路用户平均可达速率的降幅更低，对阴影衰落的鲁棒性更好.

图7 上行链路用户平均可达速率随σsh的变化情况Fig.7 Average uplink achievable rate varies with σsh

图8 上行链路用户平均可达速率随传输功率的变化情况Fig.8 Average uplink achievable rate varies with the power

图8所示为上行链路用户平均可达速率随传输功率ρ的变化情况.由图可知，随着导频传输功率增大，3种算法的上行链路用户平均可达速率都有一定程度的提高.当ρ=30 dB时，PA-MG算法相比于WGC-PD和CS算法的上行链路用户平均可达速率分别提高了 0.1 和 0.3 bit/(s·Hz).

4 结语

本文以最大化系统的上行链路可达速率为目标，提出了一种基于匹配博弈的导频分配算法PA-MG.其核心思想是：在用户侧，根据用户效用函数生成对导频的偏好列表，并向列表最优的导频序列发出分配申请；在基站侧，根据导频效用函数生成对用户的偏好列表，将对应的导频分配给偏好列表中排列最优的用户.仿真结果表明，PA-MG算法在保证导频开销较低的前提下能够有效降低导频污染，提高系统的上行链路可达速率，且各用户的信干噪比分布较均匀，对阴影衰落效应的鲁棒性更强.