模具型腔Bezier曲面精加工刀具直径自动获取方法研究*

梅 益，陈丽娅，杨幸雨，孙全龙

(贵州大学 机械工程学院，贵阳 550025 )

0 引言

随着Bezier曲面大量运用在压铸模成型型面中，其加工的质量和效率直接影响整体模具品质和生产成本。传统的加工工艺设计基本上由有经验的技术人员完成的，加工工时长，成本高，不合理的工艺设计方案给企业带来大量时间和成本的浪费[1]。在数控铣削精加工阶段，为了获得零件的准确形状、精确尺寸和良好的表面质量，往往要用合适的刀具进行精加工，刀具直径的选取是直接影响曲面加工质量的最重要工艺设计之一[2]。

国内外针对孔、槽等规则特征的识别及加工工艺获取的研究较多，花锋[3]针对槽特征在NX环境下的特征识别方法和加工工艺获取的推理机制进行了研究；刘红军等[4]对基于NX特征识别的典型孔槽类零件数控加工技术进行了研究；刘晓军等[5]对板腔特征识别及工艺获取进行了相关研究。但是，国内外针对自由曲面的特征识别及工艺获取的研究较少，尤其是针对模具中常见的Bezier曲面的特征识别及加工工艺获取研究更是鲜见文献报道。

本文经过研究提出了基于NX环境下开发了一个面向Bezier曲面的可变轴铣精加工刀具直径自动获取功能模块，该模块可实现对模具型腔中Bezier曲面进行识别，并且针对识别出的Bezier曲面自动推荐合理的精加工刀具直径参数，辅助工艺设计人员选择刀具。

1 Bezier曲面特征识别方法

Bezier曲面是Bezier曲线向曲面的直接扩展。Bezier曲线是通过一组多边形的顶点来定义的，其顶点称为控制点。第一点和最后一点固定作为Bezier曲线的起点和终点，其余的点用于控制曲线的形状和阶次。

Bezier曲线的参数向量表达式为：

(1)

式中，Pi为各顶点的位置向量，Bi,n(t)为n次的伯恩斯坦基函数。

图1 三阶Bezier曲线

设Vij(i=0,1…m；j=0,1.…n)为(m+1)×(n+1)个空间点列，则m×n次Bezier曲面定义为：

(2)

其中，Bi,m(u),Bj,n(w)是m次、n次的伯恩斯坦基函数。

图2为Bezier曲面的控制点网络，图3为图2控制点网络下的Bezier曲面，直观反映了两者之间的几何关系。

图2 3×3次Bezier曲面控制网络

图3 控制网络下3×3次Bezier曲面

基于以上对Bezier曲面的定义可知，识别Bezier曲面的关键在于识别Bezier曲线，而Bezier曲面的轮廓边界曲线就是Bezier曲线，因此可以选择基于边界曲线的特征识别方法对实体模型中的Bezier曲面进行识别。基于边界曲线的特征识别方法是从实体模型中提取与特征相关的几何拓扑信息，并与属性库中的预定义的特征类型相匹配，从而实现特征实体的识别。

在NX环境中，模型中特征的边界表示信息很容易获得，可以通过NX提供的二次开发接口NX/OPEN API封装的NX操作函数直接获得。通过UF_MODL_ask_curve_ data函数可以查询模型中边界曲线的数据信息，并且在NX属性库中预设了Bezier曲线的属性，当查询到提取的曲线的数据信息符合Bezier曲线属性时便可认定其为Bezier曲线，通过遍历几何体的方式就可以找到模型中全部Bezier曲线。仅有Bezier曲线的几何信息还不足以判断Bezier曲面，可以通过UF_BREP_ask_topology函数查询，当查询到其中2条相邻Bezier曲线从属于同一曲面特征时，可判断对应曲面为Bezier曲面，拓扑信息在UF_BREP_topology_s结构体中保存，其识别结果是模型中Bezier曲面以不同颜色标记，以告知本模块加工目标，同时给出Bezier曲面的阶次及控制点网络等基本信息，其识别流程图如图4所示。

图4 Bezier曲面特征识别流程

2 可变轴铣精加工刀具直径选择

对压铸模型腔Bezier曲面的有效识别是实现可变轴铣精加工刀具直径自动获取的基础，而建立刀具直径选择的规则模型则是刀具直径自动获取的关键。

2.1 直径选择的基本准则

由于球头铣刀在曲面铣削加工中应用最为普遍[6]，模块以球头铣刀为研究对象进行基本准则的推理。其底部为球形，铣削过程中，铣削刃和工件接触面的法线始终通过刀具的中心，使得刀具的行距计算和干涉避免计算简单化，数控编程相对简单，对加工对象的适应能力强。用残余高度h来衡量曲面加工的精度，球头立铣刀表面加工情况如图5所示。

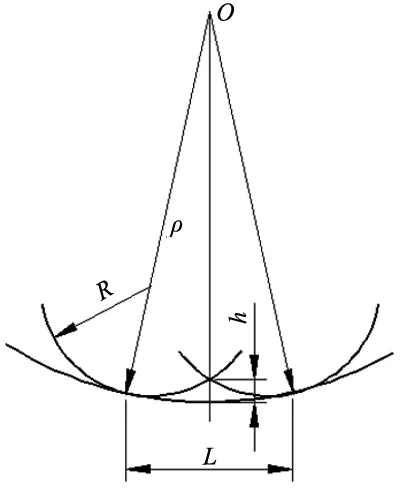
图5 凹曲面残余高度

在实际计算当中，一般ρ远大于h，因此由图5推导出残余高度h计算公式如下[7]：

(3)

式中，ρ为曲面在垂直于刀具进给方向的的法曲率半径，R为刀具半径，L为球头铣刀在当前凹面区域的加工步距。

由以上公式分析得，①球头铣刀的刀具半径必须小于曲面的法曲率半径，即R<ρ，否则刀具发生干涉，影响曲面的加工质量。②在R<ρ的前提下，刀具半径R越大，则残余高度h越小，表示表面加工精度越高。③假设残余高度h为定值时，加工刀具直径R越大，则加工步距L就越大，提高曲面加工的效率，减少加工程序量。由分析可知，在不发生干涉的情况下，应尽量选择大刀具精加工，既能提高加工质量同时也能提高加工效率。

2.2 刀具直径选择的约束研究

2.2.1 曲率干涉对刀具直径的约束

在球头铣刀加工Bezier曲面时，存在着一种干涉，刀具接触点处工件表面的曲率大于刀具回转面的曲率，即曲率干涉。而Bezier曲面，由于其局部区域几何性质的约束，无曲率干涉加工所确定的刀具直径通常较小，用小直径的刀具加工曲面上较平坦的区域，则会导致曲面加工效率较低。因此，有必要对Bezier曲面进行分区，在各个分区域，选择无曲率干涉最大刀具直径加工分区域，实现刀具的组合，相比传统曲面单一刀具加工实现提高曲面精度和加工效率的要求。

利用NX面分析函数库中的半径分析函数将图6的实体Bezier曲面零件进行分区，分区数量为5，分区效果如图6，图中右侧为不同分区曲率半径ρmin值的变化范围。

图6 Bezier曲面分区效果示例

由图6分析可知，各分区选择不同的刀具直径进行组合加工，各分区刀其直径Di应满足以下约束：

Di≤2min{ρmin}i

(4)

式中，min{ρmin}i代表第i分区中所有点ρmin值中的最小值。

2.2.2 分区曲面碰撞干涉对刀具直径的约束

另外一种干涉发生在相邻分区曲面轮廓边界线处，分区曲面轮廓边界线是相邻两分区刀具加工的极限位置，即分区曲面碰撞干涉，其干涉对刀具直径的选择影响极大。当无曲率干涉刀具加工分区面时，不会发生干涉，但是当刀具加工到相邻分区曲面轮廓边界线处，两分区曲面ρmin值大的分区曲面刀具加工极有可能对相邻分区曲面产生碰撞干涉，如图7所示。

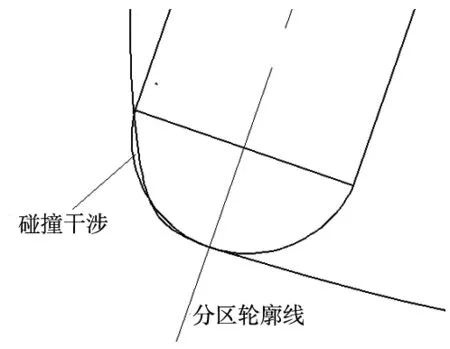
图7 分区曲面碰撞干涉示例

为避免刀具加工发生分区曲面碰撞干涉，再一次约束刀具直径加工Bezier曲面。如图8所示，k分区曲面和k+1分区曲面发生碰撞干涉。图中加工刀具正在加工第k分区，I点为分区轮廓线上的任意一点，L是过I点的任意方向截曲线，经过k分区曲面和k+1分区曲面，M法线是曲面在I点的法线，截曲线经过第k分区和第k+1分区。在M法线上取一点O,以O为圆心作圆，经过I点，且该圆与第k+1分区内的截曲线相切于唯一相切点H，确定该圆的直径为φθ，φθ称为I点在该方向截曲线上的分区曲面碰撞干涉直径。

图8 分区曲面碰撞干涉直径确定

在分区曲面轮廓边界线上I点的各方向截曲线会产生一组θ值，确定θmin作为I点的最小碰撞干涉直径，由于在分区轮廓线上存在无数个加工点，在加工第i分区曲面时，为了避免分区曲面碰撞干涉，刀具直径Di满足以下约束条件，即

Di≤min{θmin}i

(5)

式中，min{θmin}i代表第i分区曲面轮廓边界线上所有点θmin值集合的最小值。

2.3 建立刀具直径选择的规则模型

在提出组合刀具加工Bezier曲面的基础上，将刀具直径选择基本准则和刀具直径约束条件结合，构成新的刀具直径选择规则模型。

假设将Bezier曲面分为n个曲面区域，每个曲面区域的球头铣刀加工直径为D1，D2，D3...Dn，z为n个曲面区域刀具直径之和。选取刀具直径之和的最大值作为刀具直径选择的设计目标，则目标函数为：

(6)

约束条件为：

(7)

求解该模型时，在各分区曲面的刀具直径满足式(7)的基础上，实现刀具直径之和的最大值，自动求解各分区曲面加工最大刀具直径，实现多刀具的自动组合精加工。

2.4 多刀具直径组合精加工算法

在识别Bezier曲面，对Bezier曲面进行分区域的基础上，结合刀具直径约束条件，由规则模型获得的各分区曲面的最大加工刀具直径，其值是理论值，结合实际加工中企业的刀具库中的刀具直径，选择刀具库中接近最大刀具直径理论值进行精加工。具体流程如图9所示。

图9 刀具直径确定流程

3 实验验证

3.1 实验参数

以文中的Bezier曲面模型为模拟加工对象，并与传统曲面加工工艺策略加工的效果进行对比，以验证分区曲面多刀具直径加工Bezier曲面的优越性以及刀具直径选择规则模型的有效性。

在图6中，设置分区数量为5，根据直径规则模型获取各分区曲面刀具直径理论最优值，由于各企业刀具库情况不同，常用的球头铣刀直径为D4、D5、D8、D10、D12、D16等，因此实际加工刀具直径需再确定，如表1所示,表中单位均为mm。

表1 各分区曲面刀具直径及实际刀具直径确定

Dt—刀具直径理论最优值；Dn—实际选择刀具直径。

传统单一刀具直径加工Bezier曲面，刀具直径不超过Bezier曲面的最小曲率半径，因此，确定传统不分区Bezir曲面精加工的刀具直径为6mm。本模拟实验以表1推荐的球头铣刀直径Dn对Bezier曲面不同分区曲面进行精加工，同以6mm的球头铣刀直径对全局Bezier曲面进行传统精加工。

3.2 Bezier曲面模拟精加工过

确定两种工艺方案模拟加工Bezier曲面的铣削类型为往复铣，行距为0.1mm。由图10与图11可看出分区加工与不分区加工Bezier曲面加工刀轨存在明显差异，为偏差模型的建立奠定了基础。

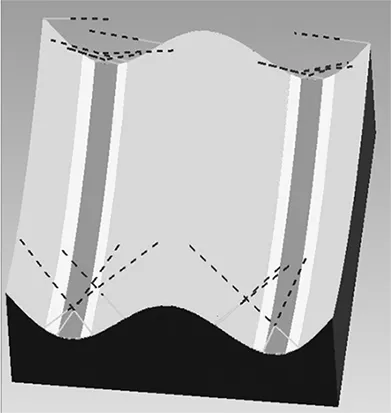
图10 分区加工Bezier曲面刀轨

图11 传统不分区加工Bezier曲面刀轨

3.3 Bezier曲面精加工偏差模型

保存两种工艺模拟加工后的Bezier曲面为IPW模型，将两个IPW模型分别与理想模型进行重合，度量两种加工工艺下Bezier曲面与理想曲面的偏差，以此来衡量Bezier曲面的表面加工质量。

图12 分区加工IPW模型与理想模型重合图

均匀的在重合图上取6条截面曲线，每条截面曲面上根据等弧长的方式取50 个点，度量全局曲面300个点位置IPW模型和理想模型的偏差，偏差图如图13所示。

图13 分区Bezier曲面全局偏差值

3.4 实验结果对比及分析

采用偏差绝对值的平均值的数学方法分别处理两个偏差模型的偏差值，平均值越小，说明Bezier曲面加工的残余高度越小，Bezier曲面加工IPW模型越接近理想模型，表面加工质量越好，数学表达公式如下：

(8)

式中，μ为一条截面曲线上各点的偏差值，σ为该截面曲线偏差值的绝对值之和的平均值。

对分区Bezier曲面IPW模型与理想模型的300个偏差值的平均值进行统计，见表2，a为图13中至上往下的截面曲线序号，b为平均值表示栏，σ为平均值。

表2 分区Bezier曲面偏差模型的平均值

由表2各截面曲线上点的σ值计算分区Bezier曲面加工全局的σ值为0.00315mm，以同样方式计算出不分区Bezier曲面上每条截面曲线上点的σ值为0.0036mm，0.0043mm，0.0043mm，0.0038mm，0.0040mm，0.0046mm，计算出不分区Bezier曲面加工全局的σ值为0.0041mm。0.00315mm<0.0041mm可知分区加工Bezier曲面在加工精度上优于传统不分区加工Bezier曲面，同时也证明了刀具直径选择规则模型的有效性。

4 结论

本文在NX环境下开发了可有效识别模型中Bezier曲面的功能模块，在此基础上，提出通过分区加工的新方法来加工压铸模成形型面Bezier曲面，并且建立了精加工刀具直径自动获取的推理机制，实现多刀具组合加工Bezier曲面。模拟实验结果表明，应用分区加工新方法和刀具直径选择规则模型推荐的刀具直径组合加工Bezier曲面相比传统单一刀具直径加工Bezier曲面在加工精度上有一定地提高。