类X-51A飞行器非定常湍流精细模拟
2019-04-08余华峰刘宏康陈树生阎超
余华峰, 刘宏康, 陈树生, 阎超
(北京航空航天大学航空科学与工程学院, 北京 100083)
一直以来高超声速飞行器因其重要的军事意义而受到世界各军事强国的广泛关注。进入21世纪以来,以超燃冲压发动机为动力的吸气式高超声速飞行器逐渐成为了高超声速飞行器中最为热门的研究领域之一。美国相继进行了X-43A[1]和X-51A[2]2款飞行器的飞行演示实验并取得成功,预示着高超声速飞行器技术在工程实用化方面取得了重大进展[3]。
吸气式高超声速飞行器由机体和推进系统高度一体化组成,其构型往往较为复杂。如美国的X-51系列飞行器包含了乘波体构型机身,吸气式冲压发动机和控制舵面等部分。而在飞行器从亚声速到高超声速飞行的过程中,存在较大迎角的爬升状态,此时飞行器前体压缩面侧缘、局部机身突起及控制舵面会诱导产生大范围的流动分离,形成复杂的分离涡结构。分离涡结构具有强烈的非定常特性,会对飞行器气动性能产生明显影响:一方面分离涡干扰破坏了舵面随迎角线性变化的气动特性,严重影响飞行器的操控性能;另一方面,分离涡脱落的低频脉动有可能与飞行器材料的结构固有频率一致引发飞行器共振,严重时甚至会造成飞行器的结构损坏。
飞行器大迎角分离流动对于数值计算方法提出了很高的要求。目前工程应用最为广泛的雷诺平均(Reynolds-Averaged Navier-Stokes,RANS)方程建立于附体边界层类型流动,对于分离流动预测精度低,难以满足精细模拟的需求[4]。直接数值模拟(Direct Numerical Simulation,DNS)虽然可以精细模拟分离流动,但目前还无法应用于高雷诺数的实际工程领域。近年来,随着计算能力的不断提升,大涡模拟(Large-Eddy Simulation,LES)以及RANS/LES混合方法被广泛应用于分离流动的数值模拟。其中分离涡模拟(Detached-Eddy Simulation,DES)类方法是目前工程领域应用最为成熟的RANS/LES混合方法之一。其在近壁区采用RANS模型,在分离区则类似于LES方法的Smagorinsky模型[5],已经在诸多复杂的工程应用中得到检验[6-7]。
国内外针对吸气式高超声速飞行器开展了一系列数值模拟研究。X-51A飞行器设计过程中曾采用CART3D和OVERFLOW软件进行了大量数值计算[2];邓艳丹等[8]建立了一个类X-51A模型,对其气动特性进行了初步研究;罗文莉等[9]研究了一种吸气式高超声速飞行器模型在大迎角下的气动特性。然而,这些研究内容大多采用RANS方法,无法获得非定常特性以及精细湍流。而近年来航空航天领域对此愈加关注,对复杂工程外形的湍流数值模拟提出了更高的要求。因此有必要开展高超声速飞行器的精细化湍流模拟研究。本文选取类X-51A外形飞行器作为研究对象,针对其在超声速大迎角状态下存在的大范围非定常分离流动现象,采用延迟DES(DDES)方法开展了精细化湍流数值模拟研究。分析其在大迎角下的分离流动特点、非定常气动特性以及壁面压力脉动规律。
1 数值方法与验证
1.1 控制方程
守恒形式的三维可压缩Navier-Stokes方程表示为
(1)
式中:Q为守恒变量;F(Fv)、G(Gv)和H(Hv)分别为3个坐标方向的无黏(黏性)通量。一般来说,Navier-Stokes求解时分别独立离散时间和空间。本文黏性通量(Fv,Gv,Hv)采用中心格式,而无黏通量(F,G,H)则采用考虑物理传播特性的Roe格式[10]。界面左右变量采用5阶WENO插值[11]得到。时间推进则采用LU-SGS格式[12],为了保证时间精度,选取双时间迭代进行计算。
1.2 DES类方法
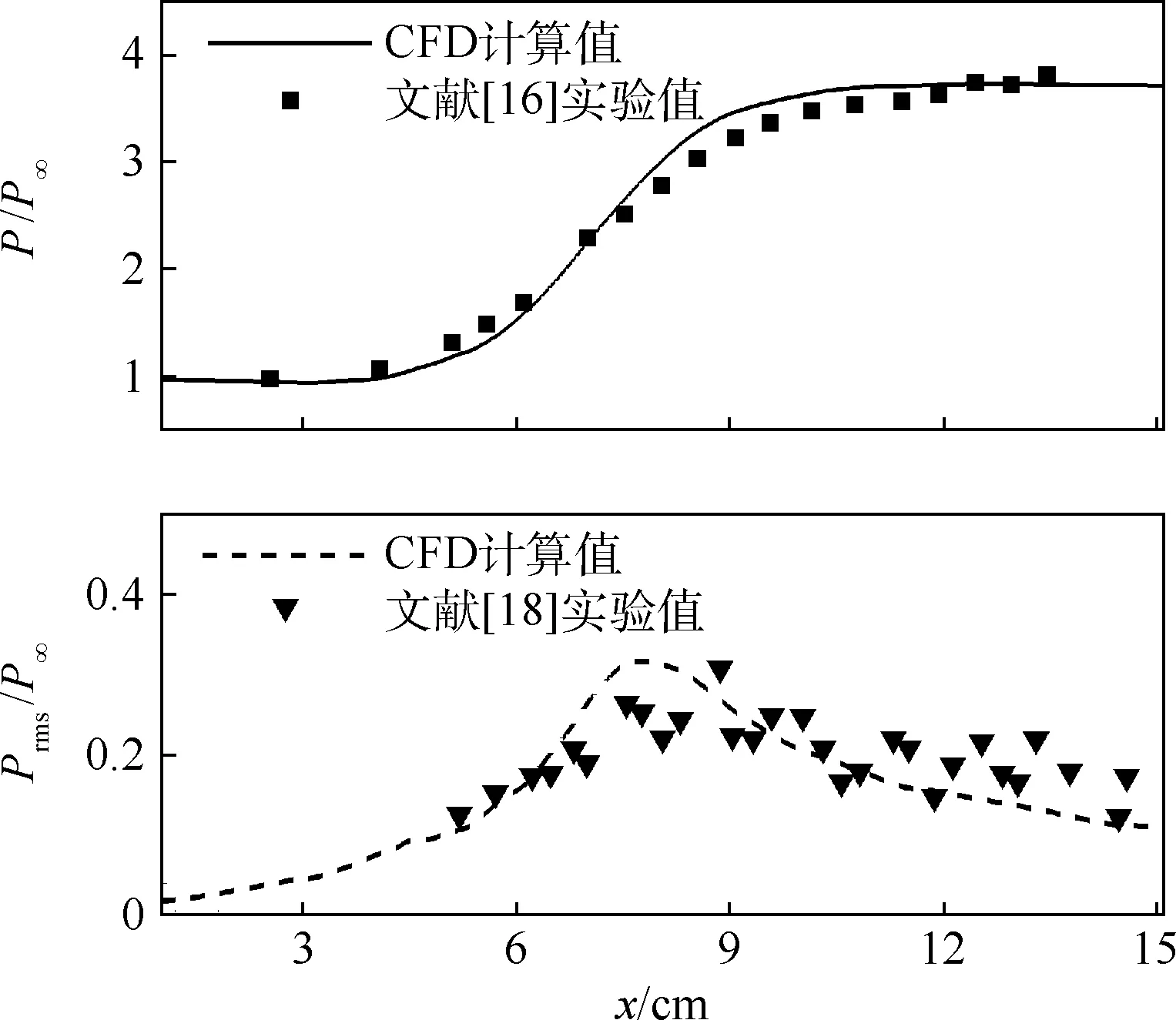
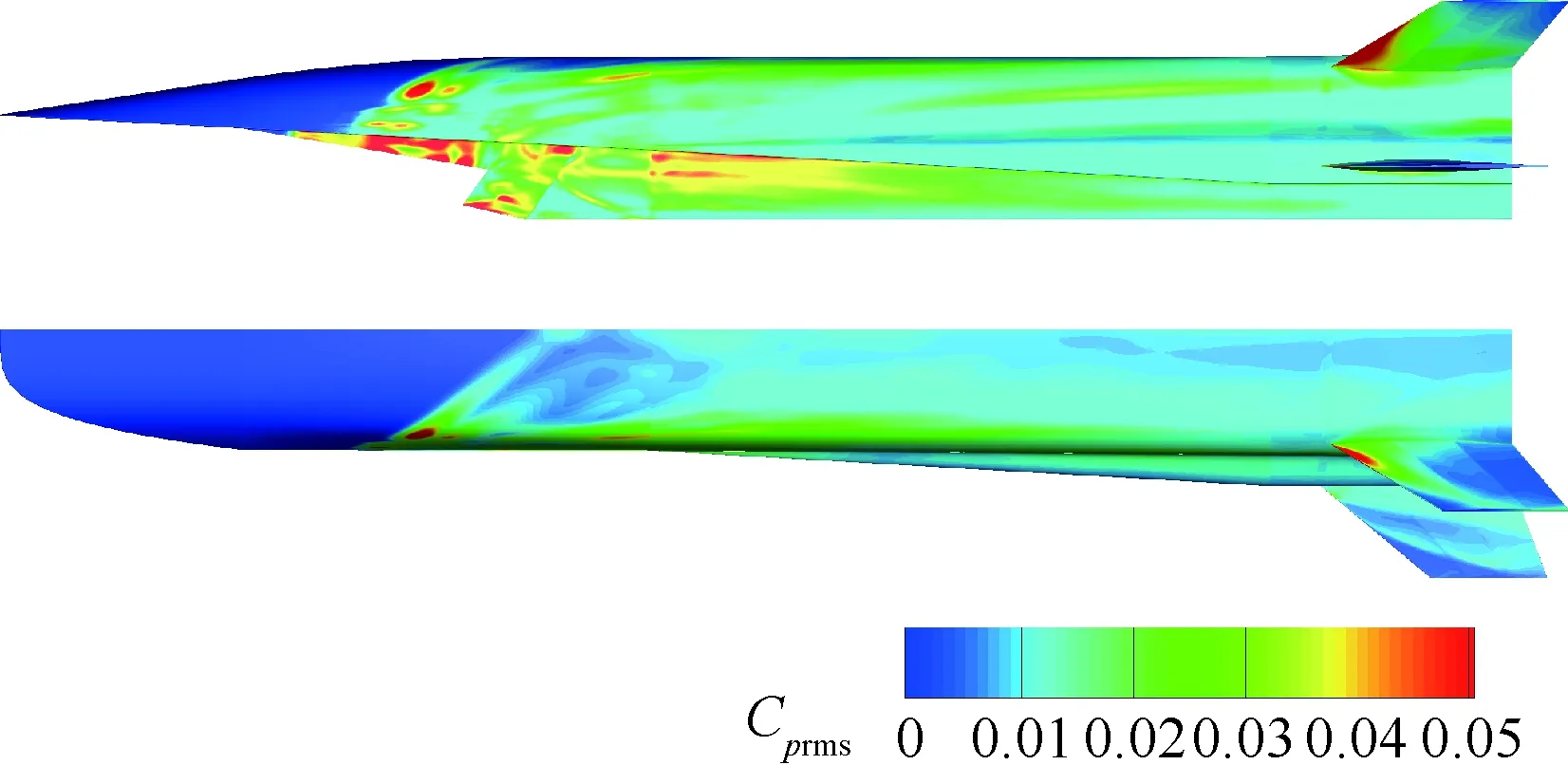
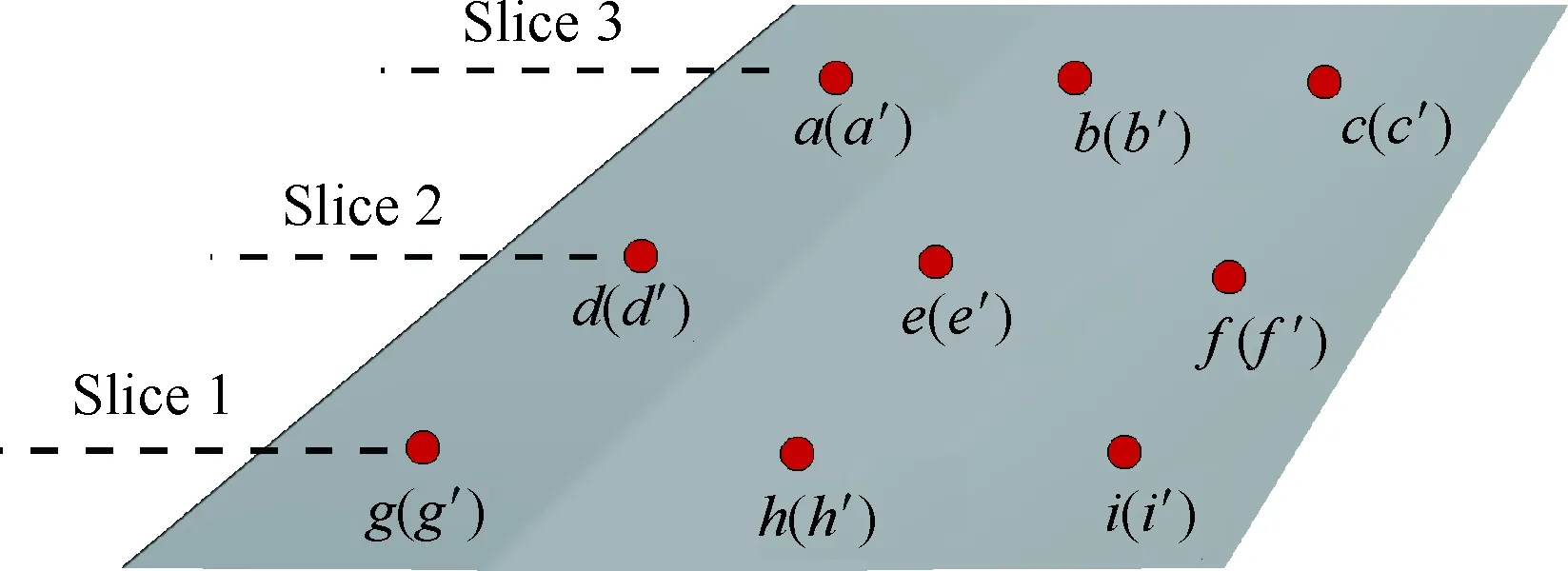
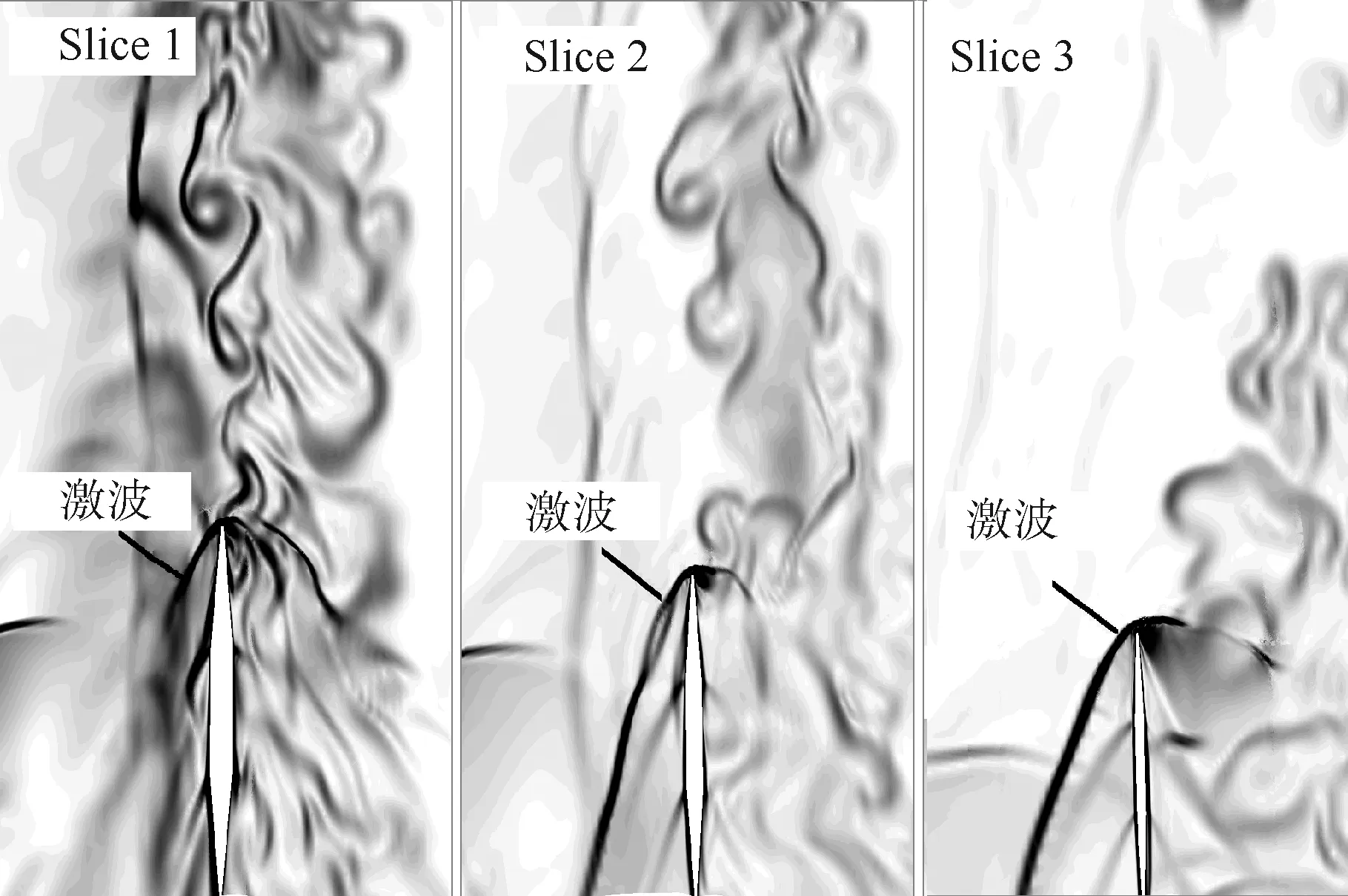
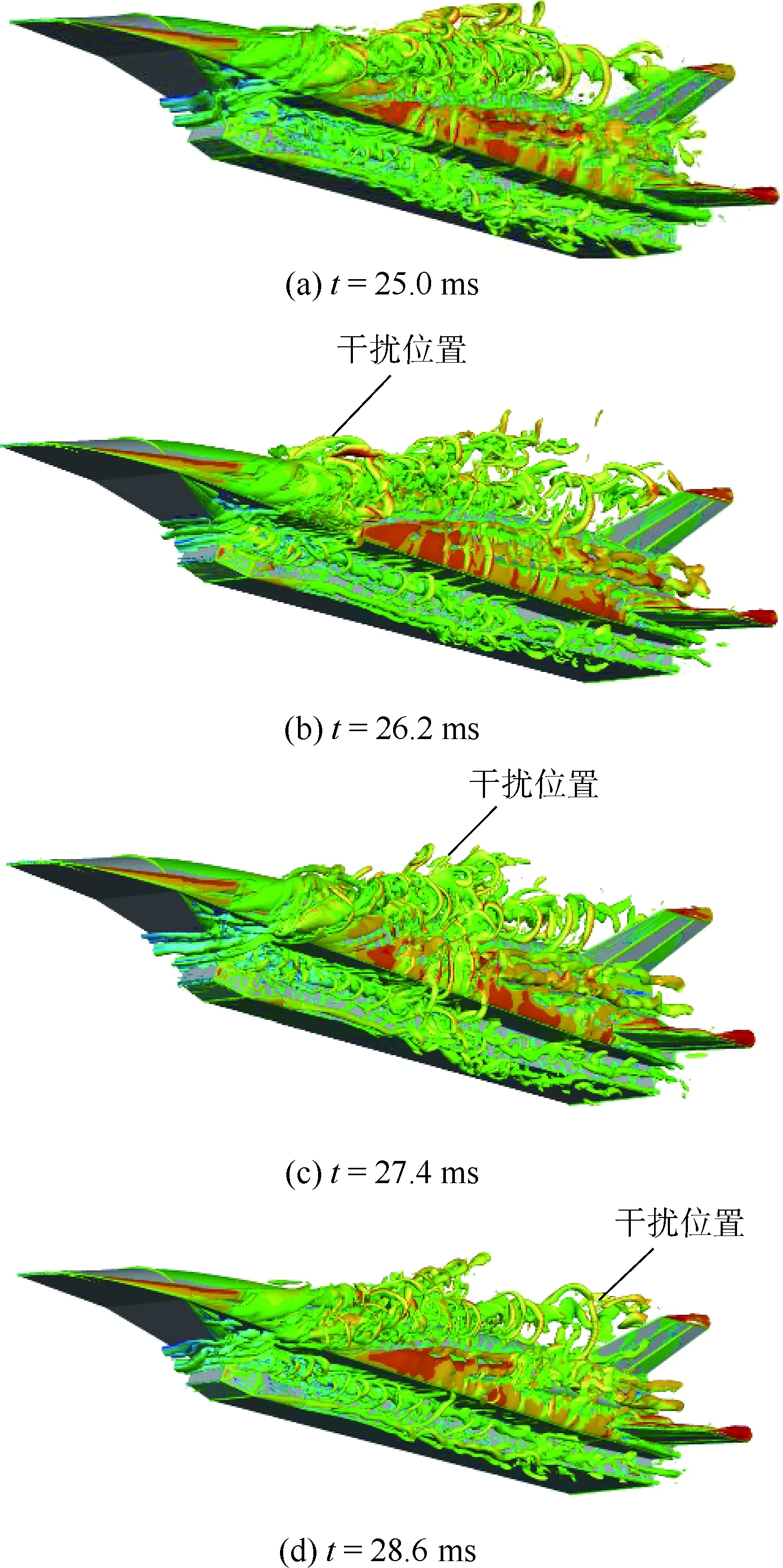
Spalart等[13]在1997年最早提出基于SA(Spalart-Allmaras)方程[14]的DES方法,其主要思想是在湍动能方程的耗散项中引入DES长度尺度LDES=min(dw,CDESΔ),其中dw为当前网格单 元中心到最近壁面的法向距离,网格尺度Δ=max(Δx,Δy,Δz),系数CDES通过算例标定,取为0.65。在壁面附近,流向与展向网格尺度一般远大于到壁面的距离,所以dw 为了验证数值方法的可靠性,本文选取斜坡空腔算例验证方法对于超声速分离再附流动的模拟能力。表1给出了算例的计算状态。关于该算例,前人做了详细的实验研究,获取了丰富可靠的实验数据。Settles等[16]给出了剪切层速度型和壁面压力系数分布;Hayakawa等[17]分析了湍流相关参数;Shen等[18]则研究了壁面压力脉动规律。计算网格如图1所示,上游和下游网格点数分别为40×55和560×155,展向长度50.8 mm,均布60网格点,总网格量为534万。通过调节上游长度确保空腔边界条件与实验一致,两侧采用周期边条。数值格式按照之前所述设置,物理时间步长为0.5 μs,总统计时长为20 ms。 首先给出某一时刻的密度梯度如图2所示,表明本文采用的模拟方法能够精细地模拟流动分离再附的结构。图3给出4个不同站位的剪切层速度型,CFD计算值和文献[16]实验值接近,较好模拟了剪切层的发展过程,其中x和y分别为来流流向距离和垂直来流向上的法向距离,空腔高度D=2.54 cm,U/U∞为当地流向速度与来流速度的比值。图4给出的是沿斜坡的壁面压力时均值以及脉动均方根,P、P∞、Prms分别为当地时均压力、来流压力和当地压力脉动均方根。对比发现无论是时均量还是脉动量都与实验吻合,表明本文计算所得的壁面压力信息具有一定可信度。因此,本文方法对于超声速分离流动模拟具有较高的精细度和准确度。 表1 计算状态Table 1 Computational condition 图1 计算网格Fig.1 Computational grid 图2 瞬时密度梯度云图Fig.2 Instantaneous density gradient contour 图3 剪切层速度型Fig.3 Velocity profiles in shear layer 图4 沿斜坡的时均压力和压力脉动均方根Fig.4 Mean and root mean square of pressure fluctuation along ramp 本文首先建立了一种类似于X-51A外形的飞行器模型,如图5所示。超燃冲压发动机安置于乘波体构型机体的下侧,飞行器前体压缩面同时也是发动机进气道的组成部分。该模型尺寸与文献[2]中给出的数据接近,能够反映X-51A这类吸气式高超声速飞行器的基本气动特征。本文主要研究飞行器纵向气动特性,模型左右对称且不考虑侧滑,所以采取半模计算。计算采用对接结构网格,对称面网格如图6所示。在网格生成时尽量满足DES类方法的要求,图7展示了部分壁面网格分布情况。由图可知在飞行器进气道入口附近以及飞行器背部等可能存在的分离流动区域保证网格具有良好的正交性、各向同性及足够分辨率,以满足相应的物理分辨率。而网格分辨率的选取主要参照斜坡空腔验证算例。在验证算例中,关键分离再附区的单位网格长度取L=0.2 mm,以空腔高度D=25.4 mm作为参考长度,则相对网格尺度Δ=L/H=0.007 87。类比至X-51A飞行器,以尾舵高度H=250 mm作为参考长度,因此单位网格长度保证在1~5 mm的量级。最终,计算网格的总网格量约为3 500万。 高超声速飞行器大迎角飞行状态主要存在于初始爬升阶段以及最终降落状态。在爬升阶段飞行器马赫较低,迎角相对较大,此状态下流动结构更加复杂。本文选取飞行器爬升阶段的一组状态参数作为计算状态,马赫数Ma=2.5,飞行高度h=18.5 km,迎角α=10°,单位雷诺数为5.84× 106/m。计算时的物理时间步长取为2 μs,计算总时长50 ms,确保流动充分发展且有足够长时间进行统计平均。 图5 计算模型Fig.5 Computational model 图6 飞行器计算网格Fig.6 Computational grids of vehicle 图7 壁面计算网格Fig.7 Wall surface computational grid 图8首先给出瞬时流场结构图(Q=200/s2等值面)。可以观测到在10°迎角下,流场中主要的漩涡结构来自于飞行器侧缘的绕流。前体压缩面附近的气流绕过侧缘卷起强烈的脱体涡。该脱体涡的漩涡破裂点相当靠前,破裂后仍保持足够强度一直向后发展,同时伴随着众多小的涡环结构的生成和耗散。此外还可以看出“V”型尾舵两侧受到干扰情况明显不同,相比之下,水平尾舵则基本没有受到干扰。这将会导致2个舵面的气动特性明显不同,具体在后面进一步分析。由于进气道入口位置的扰动,飞行器底部侧面的流动已经表现出强烈的湍流特性,存在大量的壁面湍流结构。 图9展示了流向3个不同站位的密度梯度云图,观察侧缘附近涡结构沿着流向发展的过程。x=1.5 m截面处于压缩面根部位置,此时在压缩面侧缘附近存在一个明显的分离区,但是其影响范围被限制,飞行器背部流动仍然附体;当发展到飞行器中段x=2.7 m位置时,分离区逐渐扩大,在正迎角的影响下向飞行器背部发展,有逐渐演化为脱体涡结构的趋势;在x=3.9 m位置,涡结构与 “V”型尾舵发生干扰,进而对舵面的气动性能产生影响。 图8 瞬态流场结构(Q=200/s2)Fig.8 Structure of transient flow field (Q=200/s2) 图9 瞬时密度梯度截面Fig.9 Instantaneous density gradient slices 由于分离涡的干扰,导致舵面气动性能发生了改变,比如舵面气动力系数的线性关系被破坏。为了验证这一现象,本文计算了相同状态下迎角由1°增至13°过程中飞行器舵面的气动特性。 图10给出了2个舵面的升力系数(CL)、侧向力系数(Cs),可以明显看出当迎角增大至10°以后,“V”型尾舵力系数存在明显的非线性特征,而水平尾舵则不存在这一情况。其他力系数也表现出相同的特性,限于篇幅在此没有一一给出。 侧缘卷起的脱体涡还具有明显的非定常特性,其与舵面的相互干扰会导致舵面气动力强烈振荡,可能会带来机械共振及疲劳破坏等问题。为了评估舵面力系数的脉动强度,对其进行归一化处理,显示脉动量占平均量的百分比。给出归一化后的整机和尾部舵面的脉动升力系数如图11所示,CLavg为各部件升力系数的统计平均值。受到分离涡干扰的“V”型尾舵升力系数脉动幅值达到了15%左右,明显大于整机和水平尾舵力系数的脉动幅值。 图10 尾舵升、侧力系数随迎角变化Fig.10 Variation of lift and side force coefficient of tail rudder with angle of attack 图11 升力系数脉动曲线Fig.11 Lift coefficient fluctuation curves 吴子牛等[19]指出高超声速飞行器在20~40 km高度范围内的压力脉动现象会导致飞行器表面出现局部大载荷,诱导抖振响应导致结构破坏,缩短飞行器使用寿命;同时脉动压力会造成严重的气动噪声。因此,有必要对于飞行器壁面压力脉动情况进行研究。 飞行器整体壁面压力脉动均方根分布如图12所示,Cprms为整机压力系数均方根值。飞行器前体流动附体,因此压力脉动强度不高。接近进气道入口位置,压力脉动幅值发生突越,由第2.2节瞬时流场的分析可知在该位置绕过压缩面侧缘的流动发生了分离。分离区内存在明显的非定常流动,且分离点和再附点不稳定,这些均会导致脉动压力增大。同时分离反作用于激波导致自激振荡,造成强烈低频高幅值脉动压力。相比之下,飞行器后半部分侧面的压力脉动相对减弱,与该区域主导的涡强度弱于压缩面附近的结论吻合。再观察飞行器背部,沿着侧缘分离涡的发展路径有较强的压力脉动,而靠近对称面附近区域已经远离分离涡干扰,压力脉动也相对小许多。 尾部2个舵面的非定常干扰情况相对更加复杂,图13更加清楚地展示2个舵面迎风和背风面的压力系数脉动分布情况,其中左侧为背风面而右侧为迎风面。具体有以下几个特点:①2个舵面的高压力脉动位置均处于舵前缘根部位置,主要原因是舵前缘产生脱体激波,与机身壁面附近的分离涡相互干扰,在高马赫数飞行状态下,激波较为贴体,甚至会与边界层发生干扰。激波/边界层干扰会诱导高强度压力脉动。②迎风侧压力脉动强于背风侧,主要是因为背风侧激波与壁面距离较远,不容易发生激波干扰。③“V”型尾舵的压力脉动高于水平尾舵,原因是“V”型尾舵受分离涡干扰更加强烈;可以看到“V”型尾舵背风侧高脉动区沿着舵面向上发展,对应分离涡在该位置的发展路径逐渐远离机身。 飞行器的典型蒙皮结构共振频段为100~ 500 Hz[20]。当压力脉动主频接近这个频段,其危害将会十分严重。高超声速飞行器飞行过程中由于湍流脉动、分离涡脉动和激波/边界层干扰等原因,存在不同频段的压力脉动。因此需要通过功率谱分析压力脉动的频率分布情况。图14给出了本文在计算模型“V”型尾舵上布置的监测点位置,其中括号内带上角标表示处于相同位置背风面。另外,为了方便观察“V”型尾舵附近流动结构,给出监测点所在3个截面的密度梯度云图如图15所示。由图15可知,不同截面处脱体涡与 舵前缘激波的干扰位置不同:Slice 1截面脱体涡与舵前缘激波正面干扰,导致舵根部迎、背风面的激波不稳定;在Slice 2截面迎风面激波受到的扰动相对减小;Slice 3截面前缘激波受涡干扰明显减小。 图12 整机压力系数脉动均方根云图Fig.12 Contours of root mean square of pressure coefficient fluctuation for complete vehicle 图13 尾舵压力系数脉动均方根云图Fig.13 Contours of root mean square of pressure coefficient fluctuation for tail rudders 图14 “V”型尾舵监测点Fig.14 Monitoring points on “V” shape tail rudder 图15 “V”型尾舵不同高度瞬时密度梯度截面Fig.15 Instantaneous density gradient slices of “V” shape tail rudder at different height 接下来通过图16给出了2 组监测点的压力功率谱密度(PSD)对比曲线。监测点数据采样频率为250 kHz,总采样点数为15 000,采用Burg算法进行功率谱估计。图16(a)对比了舵前缘处6个监测点a(a′)、d(d′)、g(g′)的功率谱,由图可知,a和d点迎风侧脉动能量明显强于背风侧,主要原因是迎风面激波较背风面更贴近壁面,而激波不稳定导致的压力脉动强于背风面涡结构干扰的压力脉动。相比之下处于舵前缘根部的g和g′,两点则具有接近的压力脉动强度,主要是因为舵前缘根部两侧激波受干扰强度接近。此外值得注意的是,g和g′,两点压力脉动存在明显的主频Fz=289 Hz,该频率与蒙皮材料的响应频率接近,可能对结构造成影响。图16(b)进一步展示了 “V”型尾舵根部沿流向g(g′)、h(h′)、i(i′)6个监测点的频谱。随着位置后移,压力脉动强度降低,相应的低频区域的主频在200~300 Hz的范围内,强度逐渐减弱。 图16 不同位置功率谱密度对比Fig.16 Comparison of power spectrum density at different locations 从监测点功率谱分析可知,尾舵前缘根部位置存在低频高强度脉动,针对该现象有必要进一步分析。图17展示了25.0~28.6 ms之间4个不同时刻的瞬时流场涡结构图。如图中标志所示,该段时间内,从压缩面开始产生一个展向涡结构,该结构与沿流向发展,在“V”型尾舵前缘根部位置大部分被耗散。这样的发展周期一直贯穿整个模拟过程,且频率约为208 Hz,这与舵前缘根部监测点的压力脉动主频较为吻合,可以认为该流动结构是低频脉动的主要来源。显然该周期干扰现象的源头在前体压缩面附近。图18展示了对应时刻的压缩面附近对称面马赫数分布云图。在该计算状态下,压缩面存在分离区,而分离区前缘边界不稳定,导致经过压缩面的流动周期性改变。实际上,如果飞行马赫数较低,没有达到超燃冲压发动机起动的要求,进气道入口往往会存在明显的分离泡,严重时会导致内流道产生明显振荡。显然,这样的非定常流动现象不仅会造成内流道结构的破坏,可能也会影响到飞行器外部结构。 图17 四个不同时刻Q等值面(Q=400/s2)Fig.17 Iso-surface of Q-criterion at four different moments(Q=400/s2) 图18 四个不同时刻压缩面附近对称面马赫数云图Fig.18 Ma contours of symmetry plane near compressed surface at four different moments 本文采用DDES方法对类X-51A外形高超声速飞行器大迎角爬升状态进行了非定常湍流精细数值模拟。 1) 在爬升阶段,较大的迎角会诱导飞行器侧缘发生分离以及脱体涡的形成,并且对于尾部舵面等部件产生干扰。 2) 受到分离涡的干扰,尾部“V”型尾舵表现出明显的非线性气动特性;同时舵面气动力脉动幅值明显增强。 3) 分离涡的存在导致飞行器壁面压力脉动显著增强;在舵前缘根部位置存在200~300 Hz的高幅值低频脉动,该现象由前体压缩面附近分离区不稳定导致,可能会造成结构破坏。1.3 算例验证




2 计算结果和分析
2.1 模型与网格



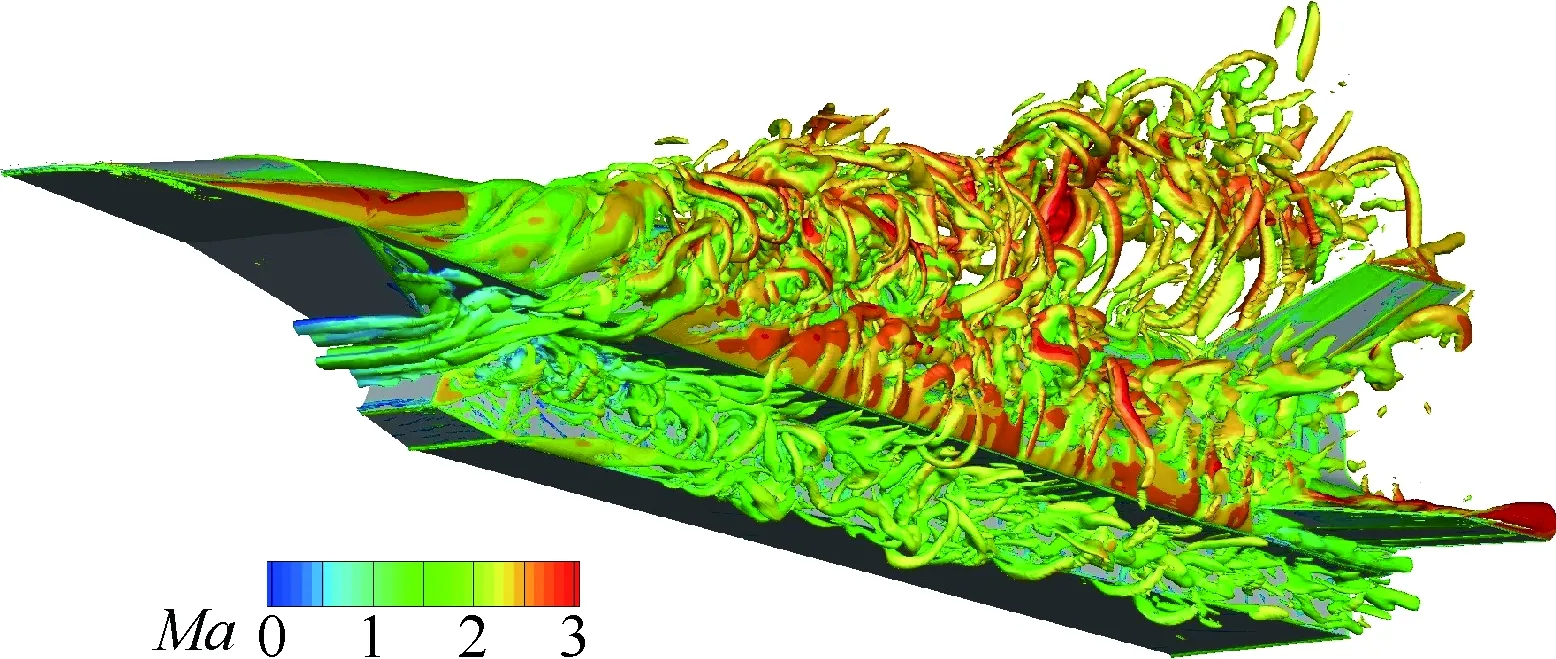
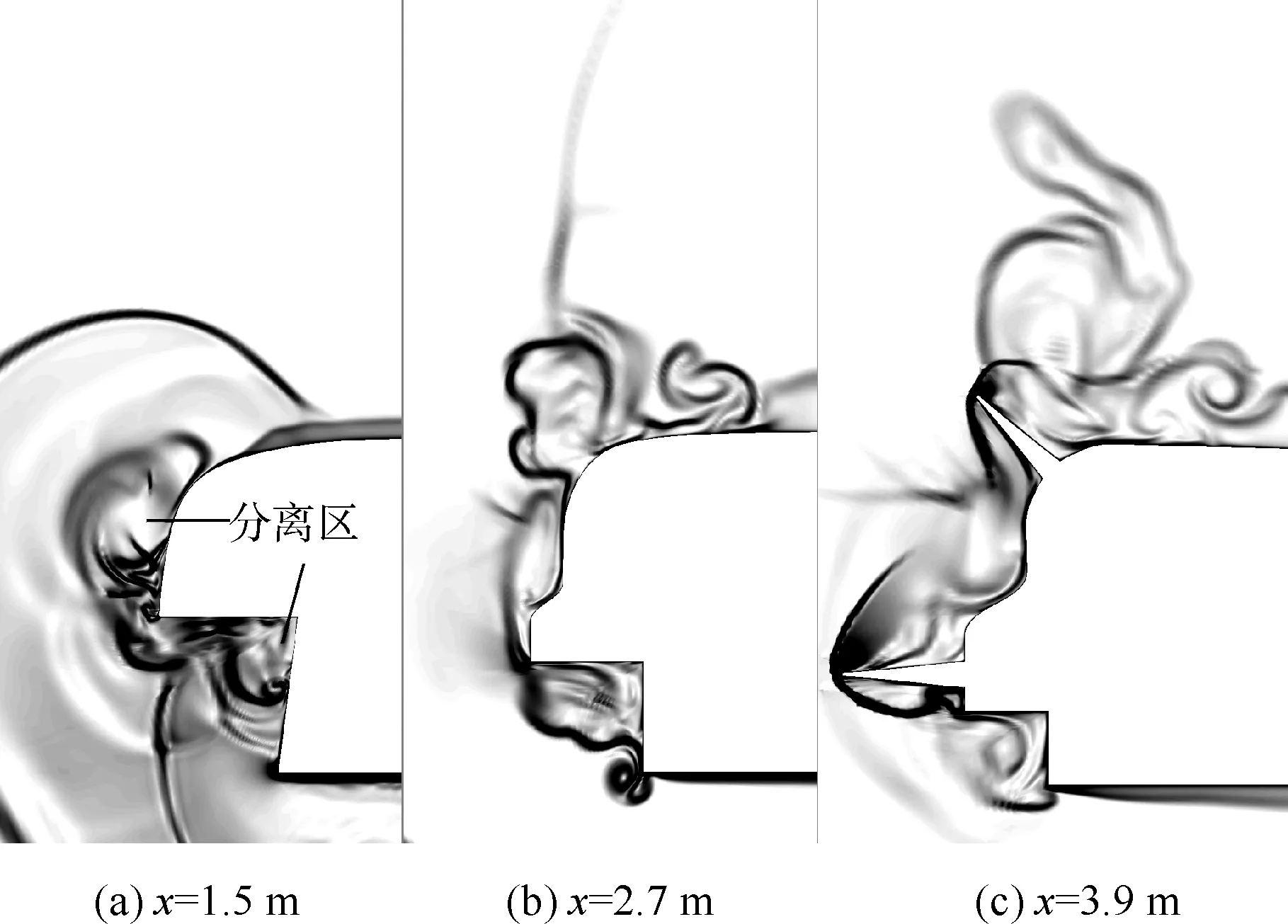
2.2 瞬时流场
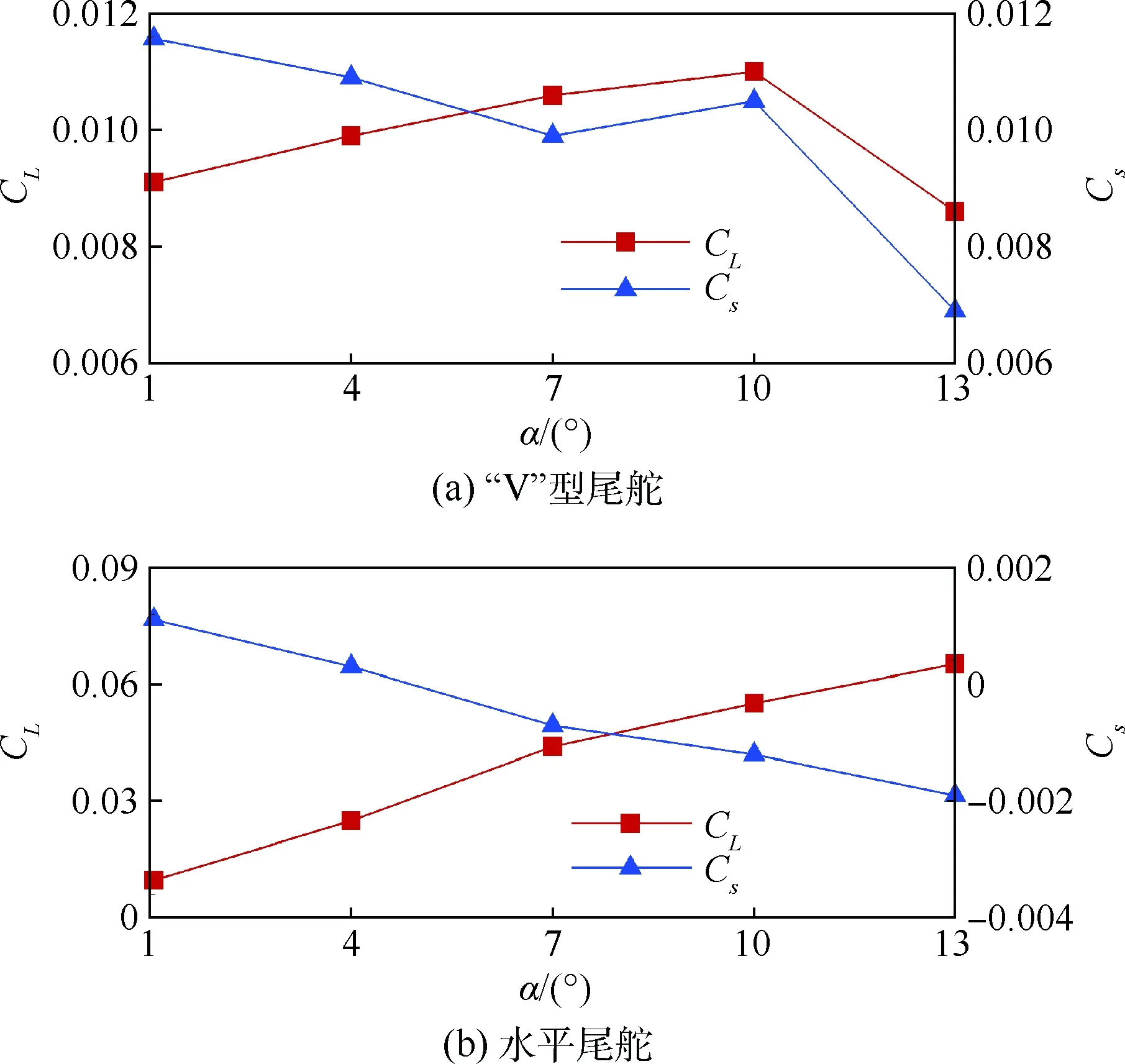
2.3 气动特性
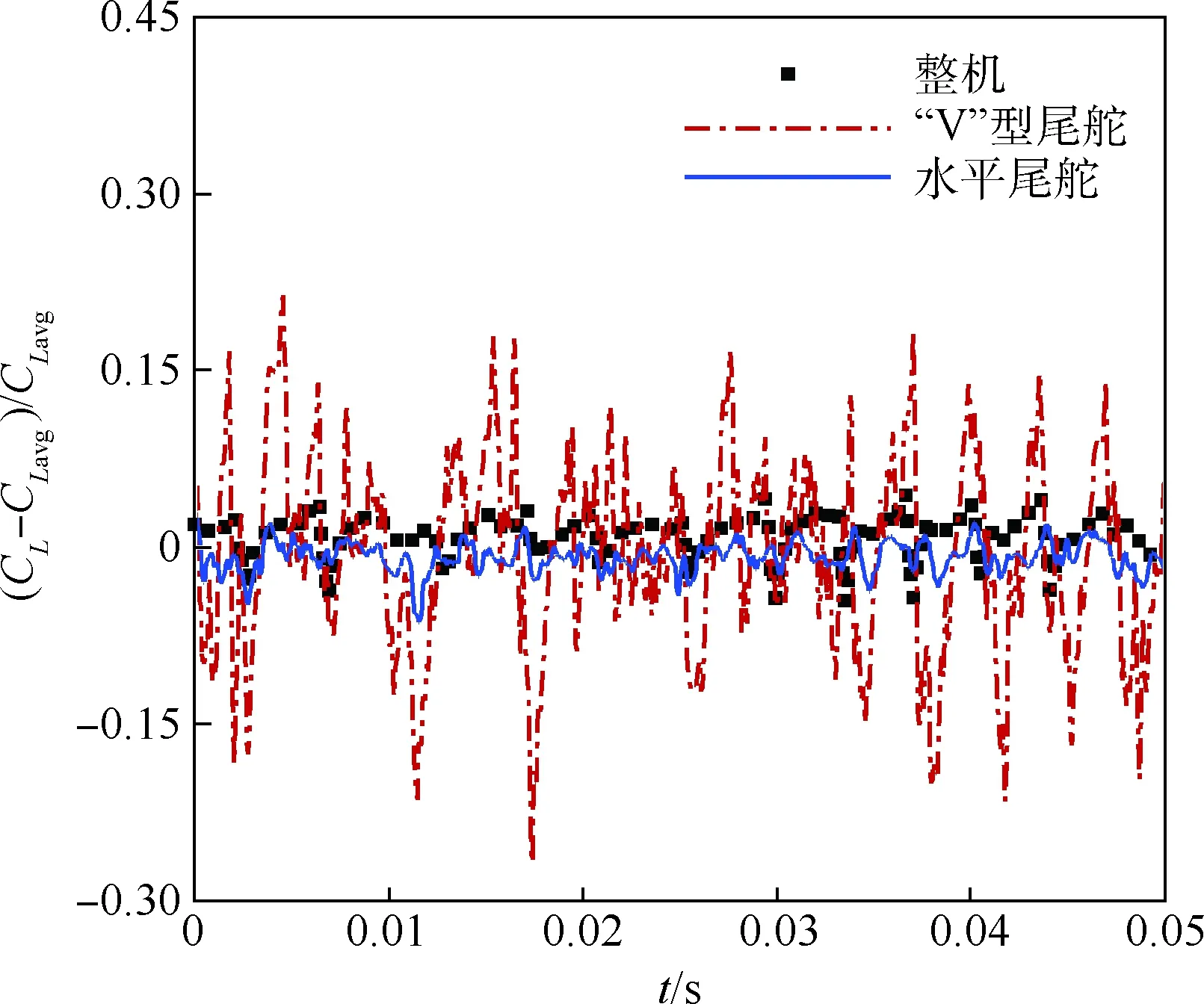
2.4 压力脉动



3 结 论
