卫星姿态控制系统执行器微小故障检测方法

李磊， 高永明， 吴止锾， 张学波

(航天工程大学航天信息学院, 北京 101416)

卫星是目前应用最为广泛的航天器，卫星的姿态控制系统故障会导致严重的后果，其中执行器由于长期处于工作状态中很容易发生故障，因此卫星姿态控制系统的执行器故障诊断问题很有研究价值。很多故障在早期表现很微小[1]，通常会被系统扰动噪声掩盖，因此微小故障的检测对于故障的早期诊断有重要意义。

基于解析模型的方法，尤其是观测器方法，在卫星姿态控制系统故障诊断中取得了很多成果，也是目前研究最为活跃的方法[2-3]。基于解析模型的故障诊断易受到扰动干扰，为解决这个问题，文献[4-5]研究了鲁棒观测器，力图使观测器残差对扰动解耦，但是由于扰动无法完全解耦，对于微小故障的检测达不到满意的效果。与鲁棒观测器类似，文献[6-8]提出的学习观测器虽然对空间干扰和测量噪声具有鲁棒性，但是也没有完全与故障残差解耦。文献[9-10]研究了自适应观测器方 法，通过对故障的自适应估计使得观测结果对扰动鲁棒，但是只考虑了输入端的扰动力矩，而没考虑测量敏感器的噪声。

鉴于解析模型难以解决扰动问题，神经网络因为其优秀的非线性建模能力被用于故障诊断。文献[11-12]提出应用神经网络对系统中的非线性部分进行估计，放宽了对系统的匹配条件，但是没有充分利用系统的结构知识；文献[13-15]提出了应用神经网络直接估计故障的方法，但是仍然没有考虑微小故障的检测问题。

干扰观测器[16-17]通常用来补偿控制系统内的模型误差等扰动，参考其补偿干扰的思路，本文提出了一种基于神经网络干扰观测器的微小执行器故障检测方法。利用卫星姿态控制系统内的冗余关系，通过构建干扰观测器对系统内的测量误差、扰动等进行估计，对基于解析模型的故障检测观测器进行扰动补偿，实现对微小故障的检测。并利用Lyapunov理论证明了所设计的干扰观测器的稳定性。

1 问题描述

1.1 姿态控制系统建模

考虑如图1所示的三轴稳定卫星姿态控制系统，其中敏感器为陀螺和星敏感器；执行器为反作用飞轮；控制算法采用非线性四元数反馈控制律。卫星姿态控制系统可以分为运动学子系统和动力学子系统[18]。运动学子系统包括陀螺、星敏感器和运动学过程，反映了卫星姿态角与角速度间的关系；动力学子系统包括反作用飞轮、陀螺和动力学过程，反映了卫星受到的控制力矩与角速度间的关系。仅考虑反作用飞轮可能出现故障的情况。

由四元数描述的姿态运动学方程为[18]

(1)

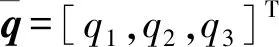
(2)

选取x1=[q0,q1,q2,q3]T为状态变量，则姿态运动学方程可以写成如下所示的状态空间形式：

(3)

式中：u1=[ωx,ωy,ωz]T为运动学输入；y1=[q0,q1,q2,q3]T为运动学输出；φ(x1,u1)为运动学非线性函数。

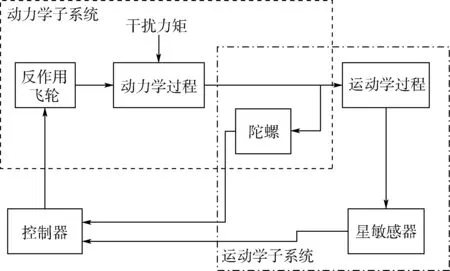
图1 卫星姿态控制系统Fig.1 Satellite attitude control system

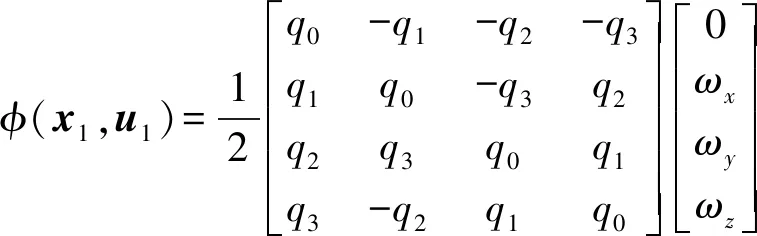
(4)

考虑陀螺的测量误差，则运动学子系统表达式为

(5)

式中：b=[bx,by,bz]T为陀螺的测量误差，包括常值漂移和随机噪声。

将卫星本体看作刚体，则由刚体运动的动量矩公式可得到卫星姿态动力学方程[18]为

(6)

式中：H为卫星的角动量；τ=[τx,τy,τz]T为卫星本体受到的合力矩在本体坐标系中的分量。

(7)

角动量H可以表示为H=IJω，其中IJ为卫星的转动惯量矩阵，通常情况下，卫星的惯性主轴与卫星本体坐标系重合时，则有IJ=diag{IJx,IJy,IJz}。考虑卫星在空间环境中受到的干扰力矩，则式(6)可以写为

(8)

其中：τc=[τcx,τcy,τcz]T为执行器产生的控制力矩；τd=[τdx,τdy,τdz]T为卫星受到的干扰力矩。

选取x2=[ωx,ωy,ωz]T为状态变量，则动力学子系统可以写成如下所示的状态空间形式：

(9)

其中：u2=[τcx,τcy,τcz]T为动力学子系统的输入；y2=[ωx,ωy,ωz]T为动力学子系统的输出；d=[τdx,τdy,τdz]T为干扰力矩；φ(x2)为动力学子系统的非线性函数。

(10)

系统的输入矩阵B、输出矩阵E和扰动分布矩阵C2表达式如下：

1.2 问题分析

在进行问题描述前，做以下合理假设。

假设1假设卫星工作在小角度机动状态下，因此式(3)和式(9)中的非线性函数均为满足Lipschitz条件的Lipschitz函数，即

(11)

假设2不同部件不会同时发生故障。

假设3故障和扰动均有界，且故障的变化速率有界。

考虑2类故障：加性故障和乘性故障。相应的故障模型为

uout=u+f

(12)

uout=(a+f)u

(13)

式中：u为正常信号；uout为故障后信号；f为故障参数，可以是一个突变常数，也可以是一个时变参数；a为某正常参数。

则故障后的动力学子系统模型可以表示为

(14)

式中：uf=[ufx,ufy,ufz]T为飞轮故障向量。

观察式(14)可知，系统中存在模型不确定性、扰动以及测量误差等干扰，因此基于故障观测器的检测方法对于混杂在干扰中的微小故障检测能力很弱。本文的工作即是提出一种基于神经网络干扰观测器的方法对系统内存在的干扰进行估计，并对故障观测器进行干扰补偿，提高故障观测器的检测能力。如图1所示，卫星姿态控制系统可以分为运动学子系统和动力学子系统2个部分。运动学子系统能反映陀螺和星敏感器间的关系，动力学子系统能反映陀螺和反作用飞轮间的关系。因此可以分别利用2 个子系统间的冗余关系对陀螺测量误差和干扰力矩进行估计，进而达到补偿故障观测器的目的。

2 微小故障检测方法

基于神经网络干扰观测器的微小执行器故障检测系统框图如图2所示，q为姿态四元数，r为检测残差。其中利用运动学子系统估计陀螺干扰；利用动力学子系统以及陀螺干扰估计结果，估计干扰力矩；最后用得到的2 个扰动估计值去补偿故障检测观测器。

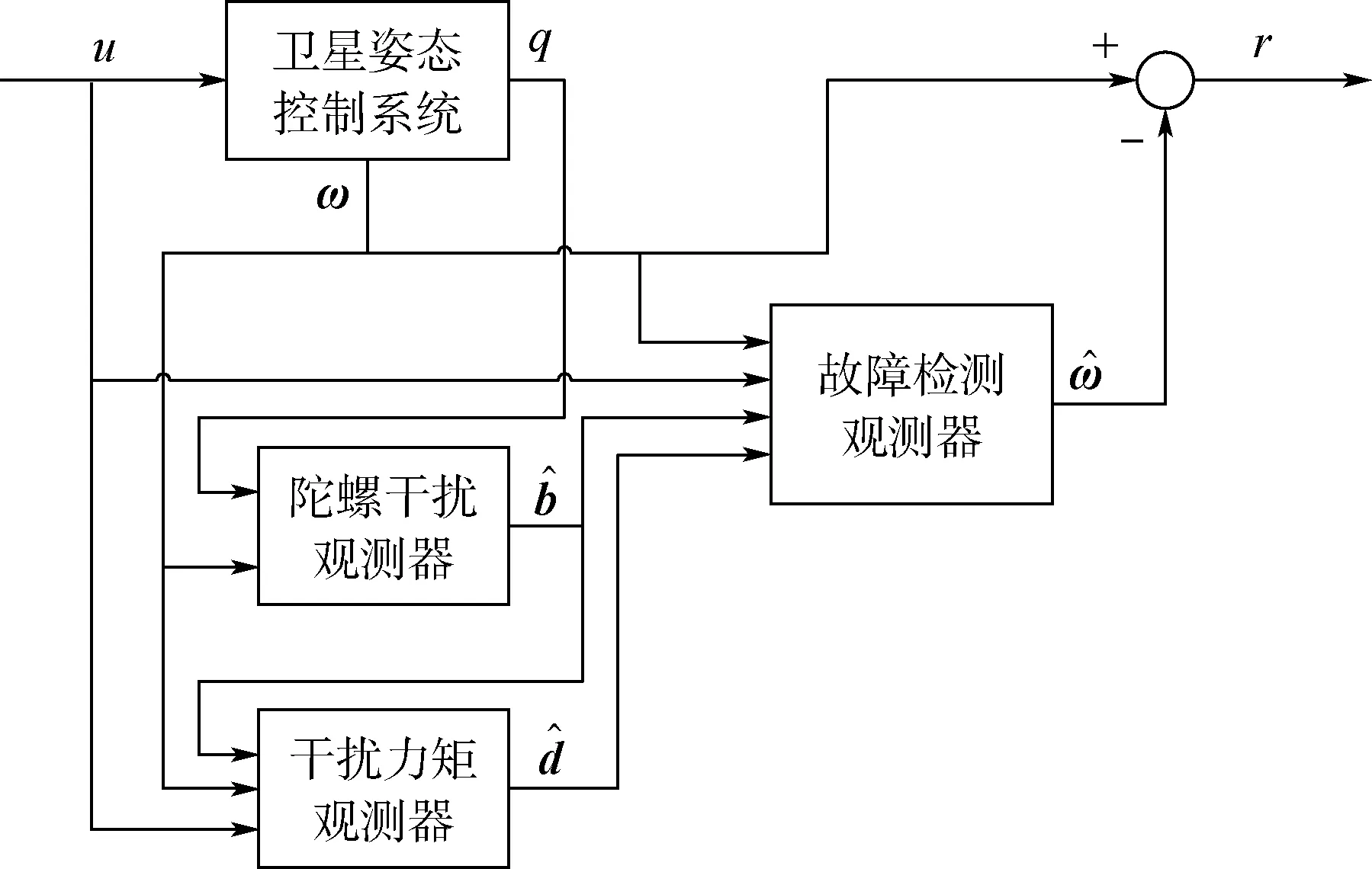
图2 故障检测观测器框图Fig.2 Block diagram of fault detection observer

2.1 基于运动学的陀螺干扰观测器设计

考虑无故障情况下的运动学子系统状态方程式(3)，采用神经网络对陀螺的测量误差进行估计，可以得到的干扰观测器为

(15)

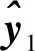
(16)

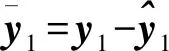
(17)

根据神经网络的逼近特性，存在一组理想权值和阈值使得b可以表示为

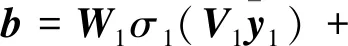
(18)

由式(5)和式(15)可以得到观测误差动态方程为

(19)

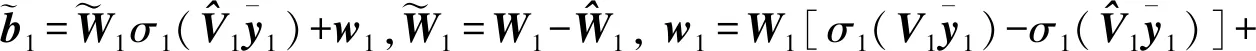
(20)

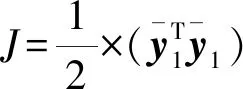
(21)

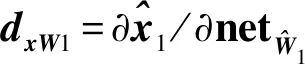
(22)

则得到最终的神经网络权值更新律为

(23)

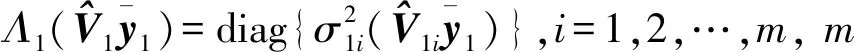
定理1考虑如式(5)的动态系统，构造如式(15)的干扰观测器，以式(19)定义观测误差。如果采用式(23)为神经网络的权值更新律，则观测误差一致有界，且神经网络权值估计误差有界。

证明选择如下正定Lyapunov函数:

(24)

ATP+PA=-Q

(25)

式中：A为Hurwitz矩阵；Q为对称正定矩阵。对式(24)进行微分可得

(26)

式中：g1(x1,u1)=φ(x1,u1)-A，由式(11)可知g1(x1,u1)满足Lipschitz条件。

(27)

将式(11)和式(27)代入式(26)，可以得到

(28)

(29)

式中：

(30)

证毕

2.2 基于动力学的干扰力矩观测器设计

考虑无故障情况下的动力学子系统状态方程式(9)，采用神经网络对陀螺的测量误差进行估计，可以得到如下的干扰观测器：

(31)

(32)

式中：隐层神经元的传递函数σ2(·)与σ1(·)相同。同样地，根据神经网络的逼近特性，存在一组理想权值和阈值使得d可以表示为

(33)

由式(9)和式(31)可以得到观测误差动态方程如下：

(34)

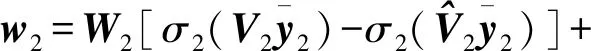
与式(23)类似，给出如下权值更新率：

(35)

定理2考虑如式(9)形式的动态系统，构造如式(31)的干扰观测器，以式(34)定义观测误差。如果采用式(35)为神经网络的权值更新律，则观测误差一致有界，且神经网络权值估计误差有界。

证明过程参照定理1。

2.3 微小故障检测观测器设计

为检测执行器的微小故障，在2个干扰观测的基础上，针对式(9)设计如下执行器微小故障检测观测器：

(36)

得到的观测误差动态方程为

(37)

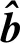
以下定理保证所设计故障观测器的稳定性。

定理3对于给定常数γ0，如果存在矩阵M和对称正定矩阵Q满足：

(38)

证明以运动学子系统故障检测观测器(36)为例，选择如下正定Lyapunov函数：

(39)

对其求导可得

(40)

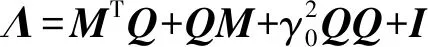
(41)

证毕

3 数值仿真分析

3.1 仿真参数设定

卫星姿态控制系统仿真框架如图1所示。控制器采用非线性四元数反馈算法，比例系数Kp=[40,40,40]T，微分系数Kd=[1 000,1 000,1 000]T。卫星的转动惯量矩阵为IJ=diag{930,800,1 070} kg·m2；初始轨道角速度为ω0=[0,1.2×10-6,0]Trad/s；初始姿态角速度ω(0)=[0,0,7.3]T×10-5rad/s；初始姿态为Q0=[0.978 6,-0.070 4,-0.179 8,0.070 4]T；干扰力矩为τd=[Axsinωdt,Aysinωdt,Azsinωdt]T，其中Ax=1.4×10-5N·m，Ay=1.5×10-5N·m，Az=1.6×10-5N·m，ωd=0.02 rad/s；陀螺常值漂移为8.72×10-5rad/s，噪声为高斯白噪声N(0,10-7)。神经网络的参数选择并没有统一的公式可循，通常参考经验公式并根据具体问题进行粗略设定，然后根据网络的表现情况进行优化。本文略去了参数的优化过程，直接给出了表现较好的一组参数。由式(16)可知，陀螺干扰观测器采用3层神经网络，其中输入层4个神经元，隐藏层14个神经元，输出层3个神经元，学习率η1=η2=20，ρ1=ρ2=1×10-7；由式(32)可知，干扰力矩观测器采用3层神经网络，其中输入层3个神经元，隐藏层10个神经元，输出层3个神经元，学习率η3=η4=10，ρ3=ρ4=1×10-6。

3.2 仿真算例

3.2.1 干扰估计

图3～图5分别为各轴受到的干扰力矩估计情况，ε为估计误差。可以看出神经网络的估计误差在100 s左右收敛到0附近，能够对干扰力矩进行很好的跟踪估计。

图6～图8分别为各轴陀螺的测量误差估计情况，bx、by、bz为各轴陀螺噪声。可以看出相对力矩干扰观测器，陀螺干扰观测器的收敛速度很快，这是因为陀螺干扰观测器中只有陀螺测量误 差为干扰源，而力矩干扰观测器中不仅在输入端存在力矩干扰，还在输出端存在测量干扰。

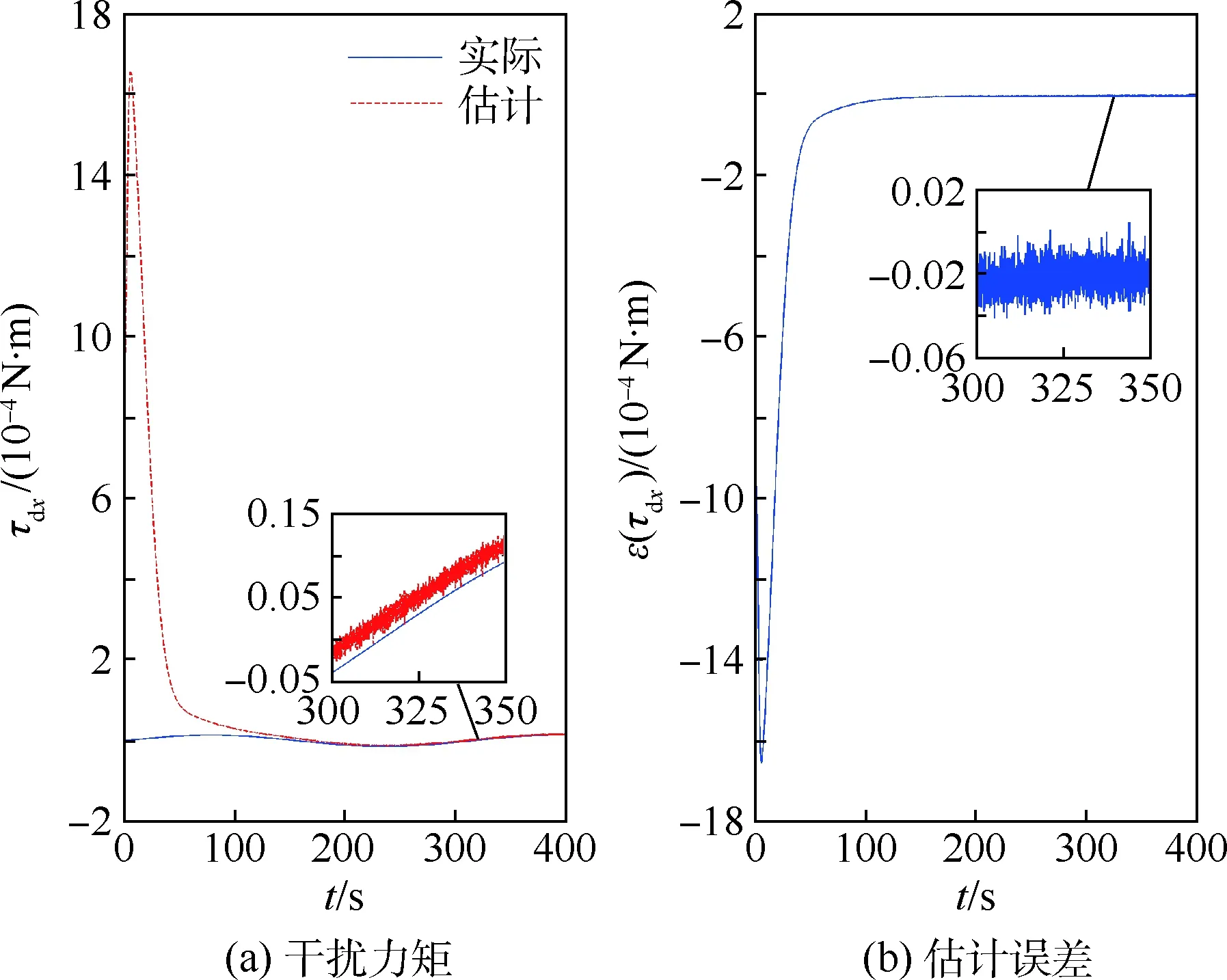
图3 x轴干扰力矩估计Fig.3 Estimated disturbance torque in x axes

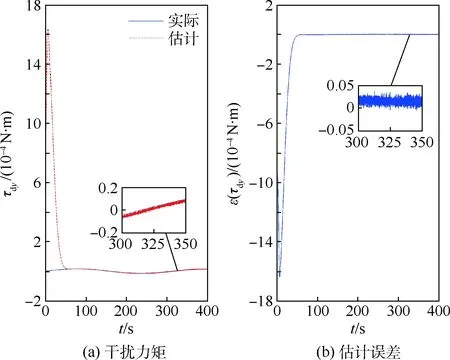
图4 y轴干扰力矩估计Fig.4 Estimated disturbance torque in y axes

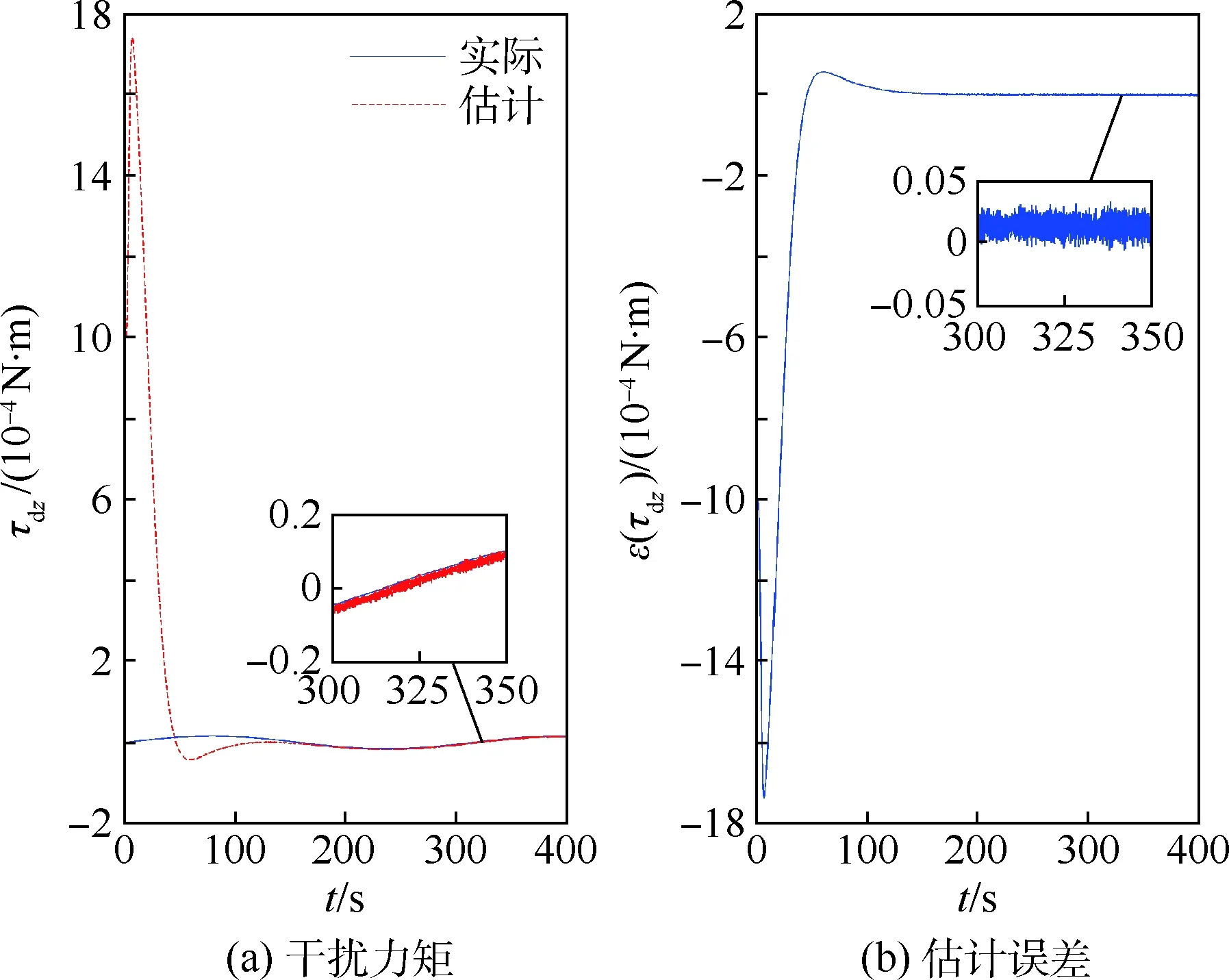
图5 z轴干扰力矩估计Fig.5 Estimated disturbance torque in z axes

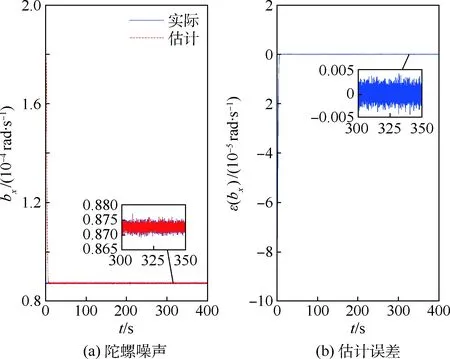
图6 x轴陀螺噪声估计Fig.6 Estimated noise of gyro in x axes

图7 y轴陀螺噪声估计Fig.7 Estimated noise of gyro in y axes

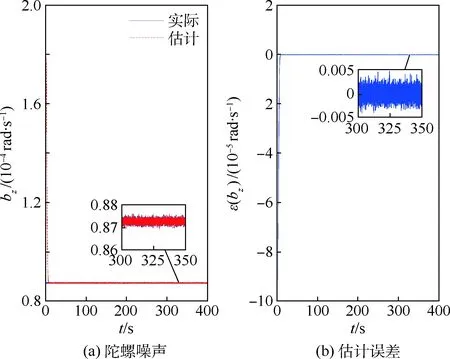
图8 z轴陀螺噪声估计Fig.8 Estimated noise of gyro in z axes

3.2.2 微小执行器故障检测

对3类不同类型故障的检测结果如图9～ 图11所示。其中，图9为对故障参数为uf1=图9(a)、图10(a)和图11(a)的结果显示，不加扰动补偿的情况下，除斜坡故障在幅值增大一定程度后可以被检测外，其他2个故障都被掩盖在扰动产生的残差中。图9(b)、图10(b)和图11(b)的结果显示，进行扰动补偿后，降低了检测阈值，且3个故障均可及时检测出来，其中前100 s为动态调整过程，不做讨论。

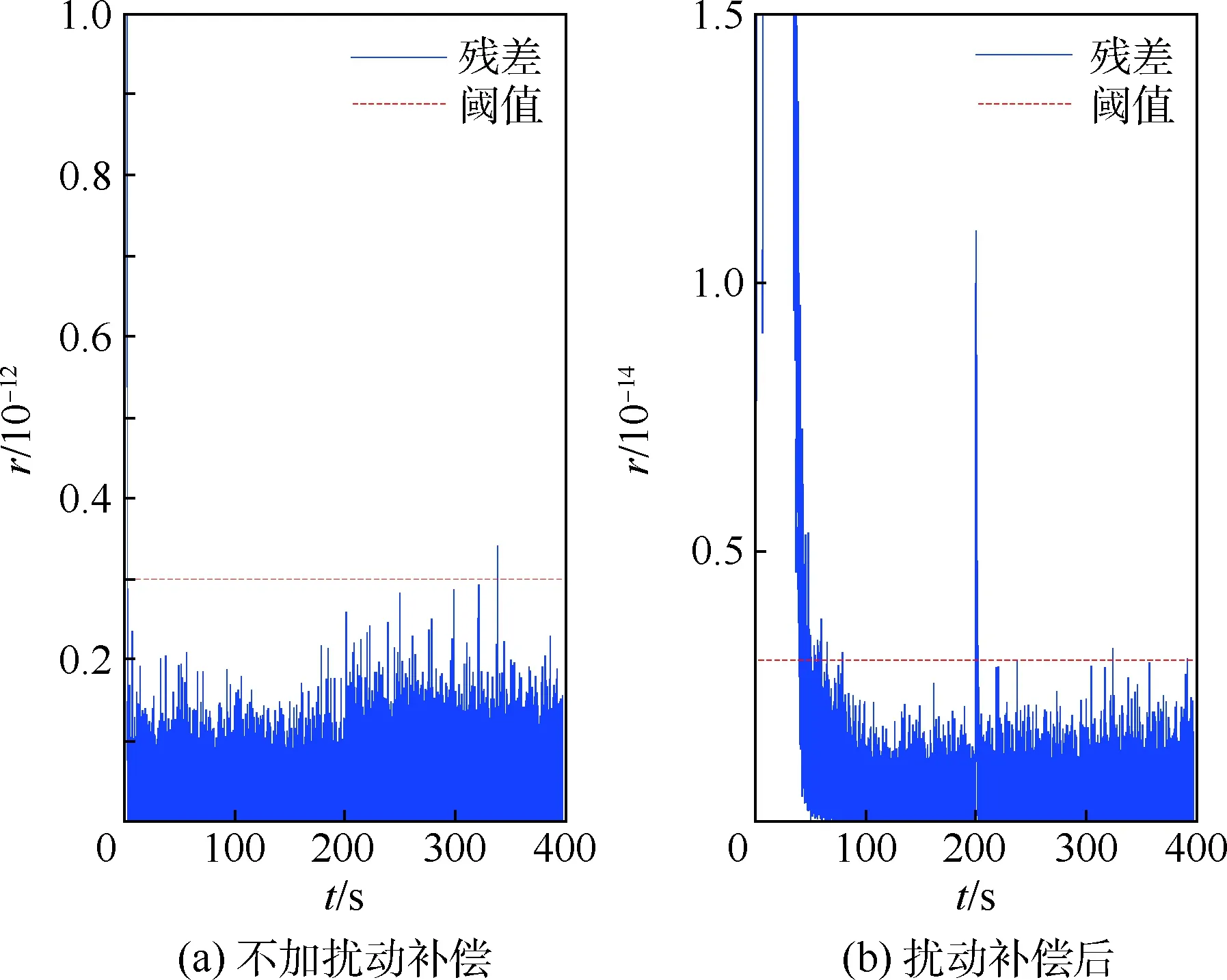
图9 故障案例1检测残差Fig.9 Detection residual of fault case 1

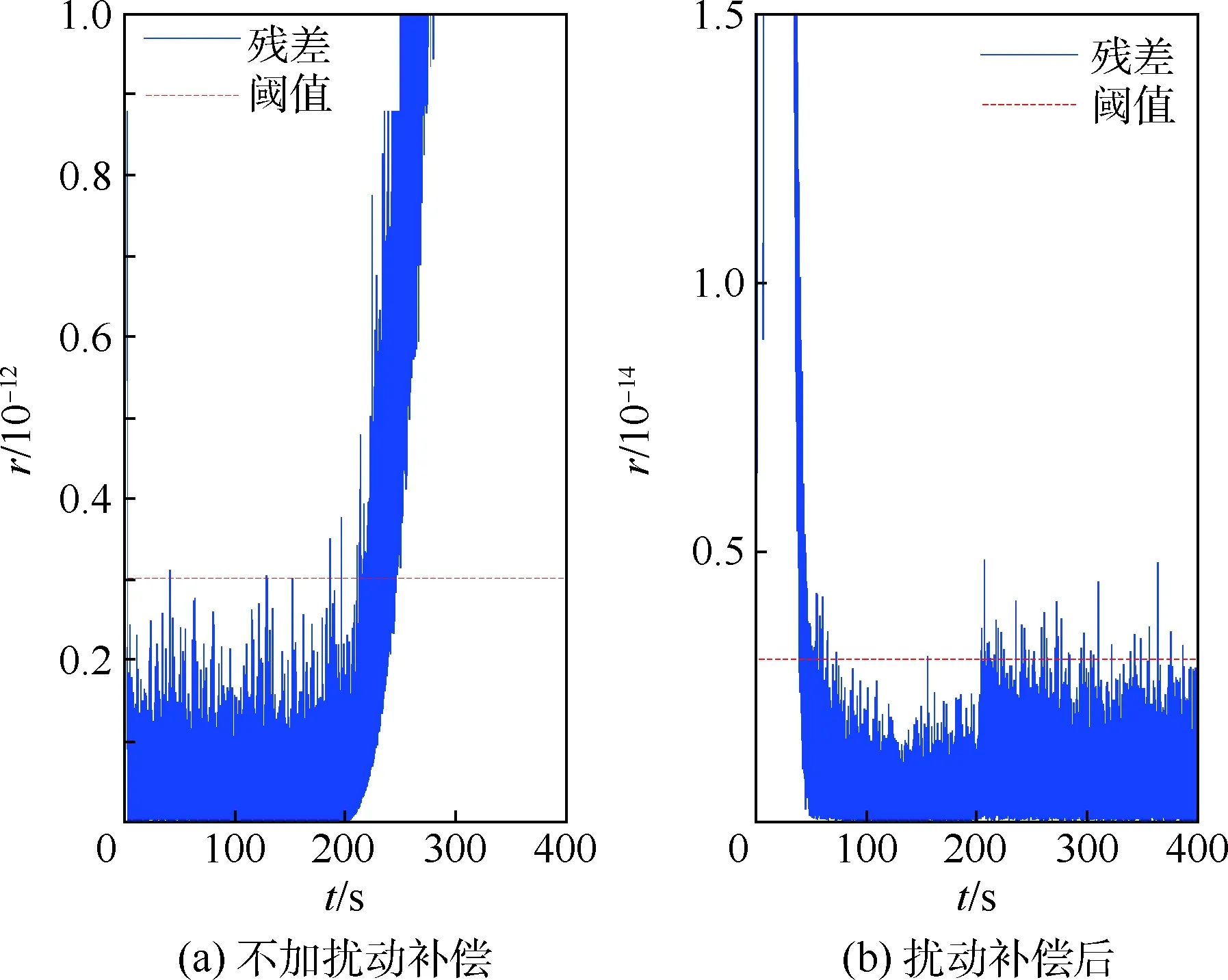
图10 故障案例2检测残差Fig.10 Detection residual of fault case 2

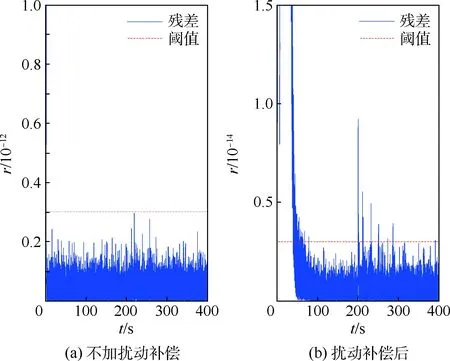
图11 故障案例3检测残差Fig.11 Detection residual of fault case 3

由3个不同故障案例的检测结果来看，该方法解决了微小执行器故障的检测问题，但是不能解决故障的隔离、诊断问题，后续还需要进行故障隔离观测器等工作。

4 结 论

1) 通过利用姿态控制系统内冗余关系设计干扰观测器，对故障检测器进行扰动补偿，从而实现了对微小执行器故障的检测，但是不能进行故障隔离等。

2) 干扰观测器采用神经网络进行设计，证明了采用的自适应权值更新律能够保证观测器的稳定性；证明了扰动补偿下的故障检测观测器的稳定性。

3) 以3 轴稳定卫星姿态控制系统为例，仿真了本文方法对不同类型的微小执行器故障的检测能力，并与未进行扰动补偿的情况进行了对比。