激发跃迁速率对热力学非平衡氮气紫外辐射的影响

吴杰， 余西龙， 段然， 朱希娟， 李霞， 马静

(1. 中国科学院力学研究所高温气体动力学国家重点实验室， 北京 100190; 2. 中国科学院大学工程科学学院， 北京 100049; 3. 光学辐射重点实验室， 北京 100854)

在飞行器再入大气时的热防护问题研究中，高温非平衡空气的辐射加热作用十分重要[1- 4]。而要计算再入高超声速绕流场的辐射首先需要确定热力学非平衡状态下空气中原子、分子的能级分布情况。因为此时原子、分子能量交换的弛豫时间与高超声速的流动特征时间可比拟，所以振动温度、平动温度、转动温度无法达成一致，各自由度能级分布偏离Boltzmann分布。

对于高超声速流动过程中的热力学非平衡分子能级分布，一般认为分子的振动、转动能级满足各自温度下的Boltzmann分布，而电子能级则会明显偏离电子温度的Boltzmann分布，后来也有人认为振转能级也会偏离Boltzmann分布[5]。对于无法用温度简单描述的能级分布情况，目前主要采用碰撞-辐射(Collisional-Radiative，CR)模型计算能级分布[6-7]。CR模型通过计算各类能够影响能级数密度的微观过程速率，从而建立控制方程，来计算各能级分布。求解过程中，认为能级分布计算可以与流场计算解耦，同时假设能级变化处于准稳态(QSS)。影响CR模型精度的最大因素就是对各能级跃迁微观过程速率的描述。许多人通过量子力学ab initio的方法或实验测量的方法获取这些跃迁的速率，但是不同方法得到的速率一般都有巨大差异[8-9]。

1 理论模型

1.1 碰撞-辐射模型

对于不满足Boltzmann分布的分子能级分布，一般采用建立速率方程的方法计算各能级的数密度。速率方程需要考虑影响多种能级的激发、退激过程，包括电子碰撞激发、重粒子碰撞激发、自发辐射跃迁、碰撞离解。

建立速率方程如下：

(1)

式中：Ni为i能级数密度，cm-3；Ne为电子数密度，cm-3；K(i,j)为碰撞跃迁速率，cm3/s；N+为离子数密度，cm-3;K(i,c)为碰撞离解速率，cm3/s；A(i,j)为自发辐射跃迁速率，s-1。

对该方程的求解基于QSS假设，认为各类激发过程的速率一般远大于i能级数密度的变化率，因此认为

(2)

速率方程简化为一般的代数方程，可方便地进行求解。

1.2 碰撞激发速率模型

(3)

式中：m为碰撞粒子质量；T为温度；σ为激发截面积；E为碰撞能量;k为Boltzmann常数。Park[6,11]在1984年公布的NEQAIR代码中使用类氢粒子的非弹性碰撞模型计算了碰撞激发截面积，并得到了激发速率系数。2008年，Park[12-13]基于实验测量数据对激发截面积进行了修正。1999年，Teulet等[14]基于WTCS(Weighted Total Cross Section)方法计算了双原子分子与电子碰撞的激发和离解速率。2006年，Johnston[15]基于Teulet的理论模型，结合最新的实验测量结果选取了一套分子与电子、重粒子碰撞激发、离解的速率系数。

图电子态的碰撞激发速率系数随温度的变化Fig.1 Variation of electron collision excitation rate coefficient from state with temperature

在本文分析的激波管实验中，重粒子的数密度比电子约大3个量级。从图1可以看出，重粒子碰撞激发的效果与电子碰撞同等重要，需要同时考虑[16]。对于不同的速率系数模型，同一状态下的激发速率系数差别是很大的。如果激发速率过大，仿真结果将始终处于平衡状态，无法反映恰当的非平衡效应发生过程。而如果激发速率过小，针对平衡态的仿真结果也将偏离Boltzmann分布，背离真实情况。

2 理论仿真和对比

本文模型仅考虑分子电子能级的Non-Boltzmann分布，认为振转能级均满足Boltzmann分布。

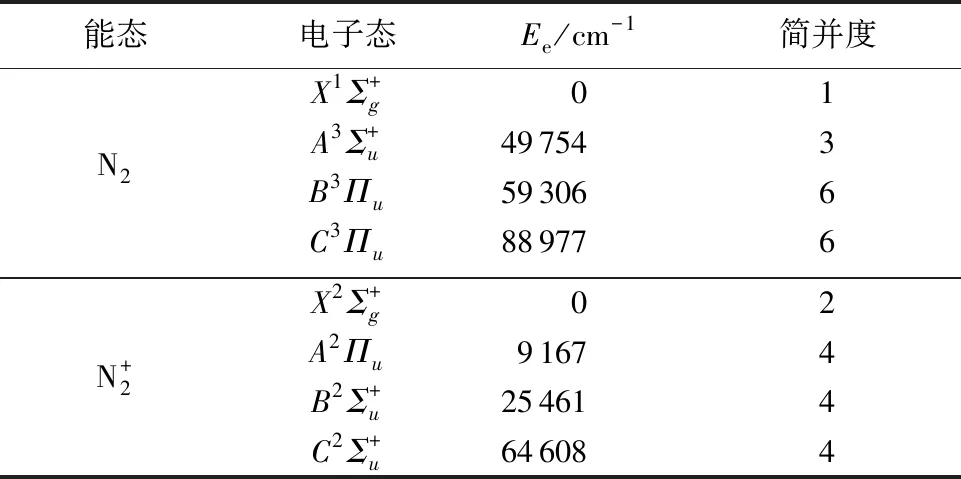
表1 计算考虑电子能态Table 1 Electronic states in calculation

2.1 平衡区辐射光谱

基于流场计算结果，平衡区温度为6 464 K。基于分子电子能级的Boltzmann分布,采用逐线法[17]计算分子的辐射光谱与实验测量结果对比如图2所示。

在380～390 nm的位置，辐射光谱受到激波管中常见的杂质CN的Violet谱带影响，本文假设CN物质的量浓度为8.5×10-6，得到了与实验结果较为匹配的辐射光谱。

采用CR模型对平衡态下的能级分布开展计算，得到能级分布如表2所示，Nie为能级i三温度Boltzmann分布下的能级数密度，Ni为能级i非平衡能级数密度。

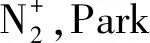
图2 平衡区测量与计算辐射光谱Fig.2 Measured and calculated radiation spectra in equilibrium area

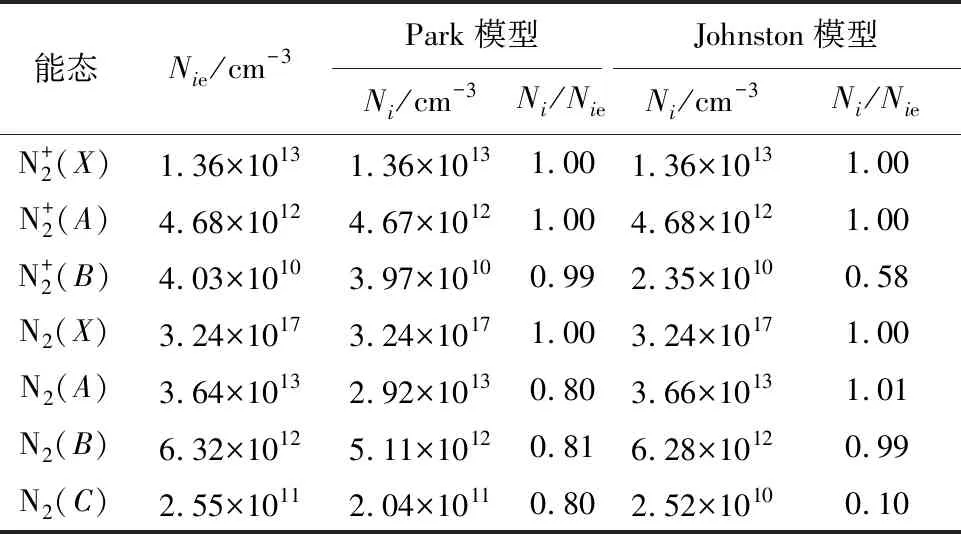
能态Nie/cm-3Park模型Johnston模型Ni/cm-3Ni/NieNi/cm-3Ni/NieN+2(X)1.36×10131.36×10131.001.36×10131.00N+2(A)4.68×10124.67×10121.004.68×10121.00N+2(B)4.03×10103.97×10100.992.35×10100.58N2(X)3.24×10173.24×10171.003.24×10171.00N2(A)3.64×10132.92×10130.803.66×10131.01N2(B)6.32×10125.11×10120.816.28×10120.99N2(C)2.55×10112.04×10110.802.52×10100.10

2.2 非平衡区辐射光谱

在激波管实验中非平衡区域的物理状态下，不同模型碰撞激发速率系数如表3所示。

Park模型认为N2的C3Πu能级由于具有接近离解限的电子能级，其能级分布应该与N原子达到离解平衡，满足Saha方程，不需要参与到速率方程的求解中。因此并没有计算与C3Πu能级相关的激发速率。

按上述能级分布计算的辐射光谱与实验测量结果的对比如图3所示。

2.3 速率系数

表3 不同模型碰撞激发速率系数的计算结果Table 3 Calculation results of collision excitation rate coefficient by different models cm3·s-1

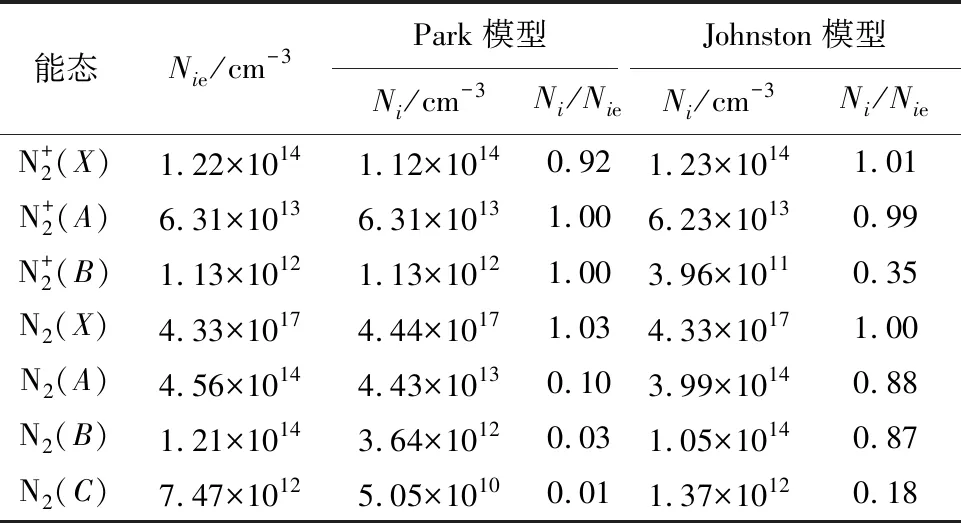
表4 不同理论模型计算的非平衡区分子电子能级数密度

图3 不同理论模型计算的非平衡区域辐射光谱与实验测量结果比较Fig.3 Comparison of nonequilibrium radiation spectra calculated by different theoretical models with experimental measurements

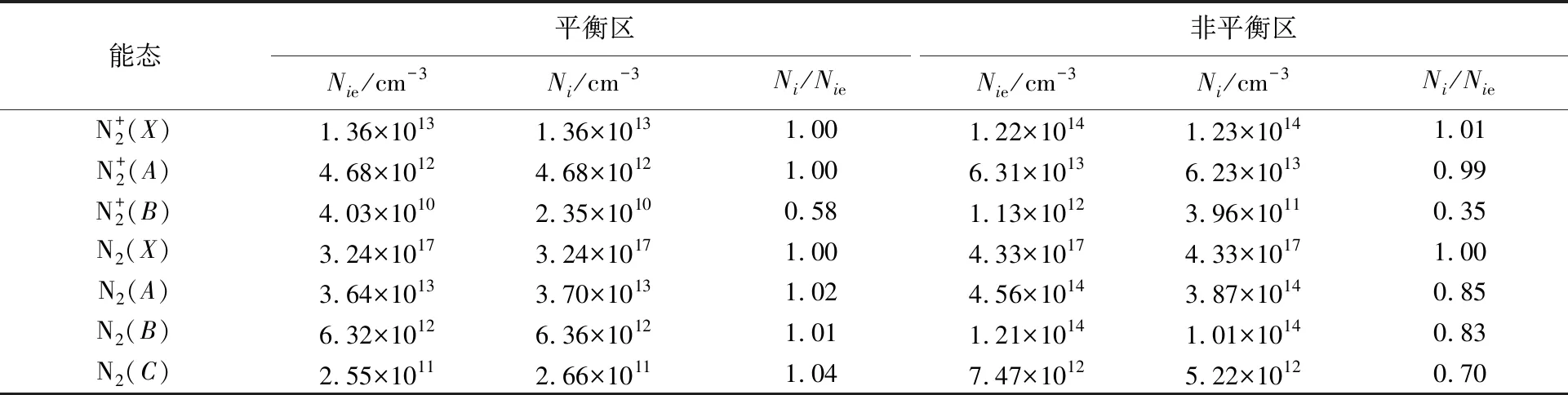
表5 修改后的速率模型计算的分子电子能级数密度Table 5 Molecular energy level density calculated by modified rate model

将Park模型的爱因斯坦系数代入Johnston模型后，在平衡区能够得到Boltzmann分布。在非平衡区按照表5的能级分布，计算得到的光谱如图4所示。

经过修改之后采用Johnston参数的CR模型可以得到更接近实验结果的辐射光谱，尤其在谱带峰值位置与实验测量结果有较好匹配，只在谱带侧翼偏差较大，如300～310 nm波段。

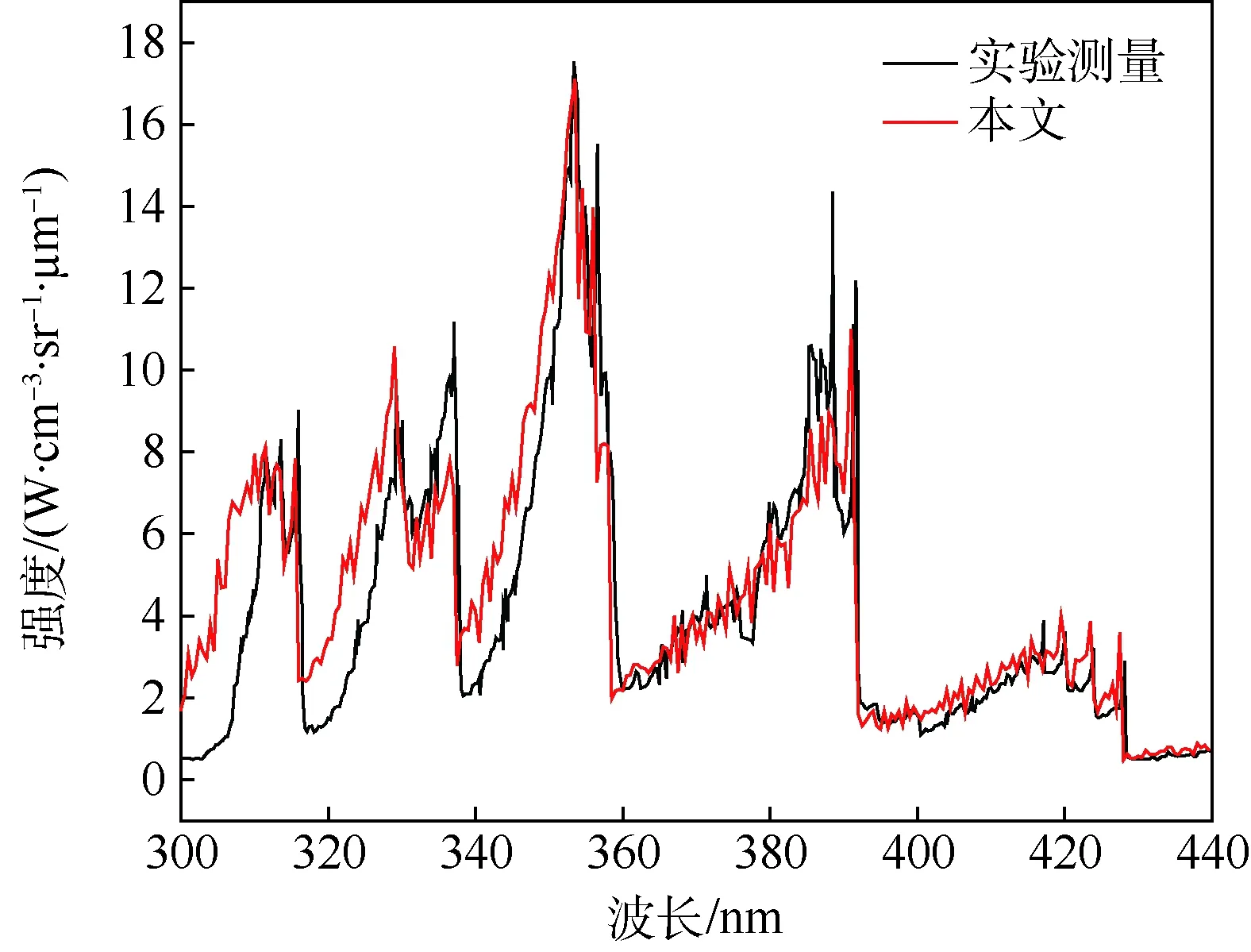
图4 采用修改模型计算的非平衡区域辐射光谱与实验测量结果比较Fig.4 Comparison of radiation spectra of nonequilibrium area calculated by modified model with experimental measurement results

3 结 论

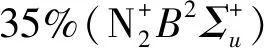
2) 为描述激波中的非平衡过程，需要引入对微观过程精细计算的CR模型，而CR模型的精度就很大程度上依赖于各微观过程速率的精度。通过本文的工作可以发现，Park模型对各类碰撞激发过程的速率都有过高的计算，使得即使在非平衡区域也很难仿真出偏离Boltzmann的能级分布。Johnston模型通过收集各类实验与仿真的激发速率得到相对较好的速率参数集，但是对N2(C)⟹N2(B)+hv自发跃迁过程爱因斯坦系数的错误设置极大地影响了仿真的光谱结果。本文发现，综合Park模型的爱因斯坦系数和Johnston模型的碰撞激发速率可以得到与激波管实验最为匹配的理论计算结果。