基于改进RRT算法的窄通道路径规划
2019-04-07白利征阎鑫齐少璞赵守智
白利征 阎鑫 齐少璞 赵守智

摘 要:RRT算法是一种经典的路径规划算法,但对于存在窄通道的环境,其执行速度较低。本文进行了一些改进,先缩小物体找到粗略路径,再采用双桥测试识别路径附近的窄通道区域,增加其中的采样密度,并采用动态步长,使采样步长随區域和碰撞情况自适应调整,提高了窄通道环境中RRT算法的运行效率。
关键词:快速扩展随机树 窄通道 动态步长 双桥测试法
中图分类号:TP24 文献标识码:A 文章编号:1674-098X(2019)11(b)-0027-02
快速扩展随机树(rapidly exploring random tree,简称RRT)算法是由美国爱荷华州立大学的Steven Lavalle教授在1998年提出的[1],在路径规划中已经获得广泛应用。但在有窄通道的复杂环境中,由于障碍物之间距离狭小,落在窄通道中的采样点相对较少,经典的RRT算法将难以找到路径。
为解决窄通道环境路径规划的难题,国内外已有大量研究。例如Hsu D等人提出了一种桥测试法,首先正态分布生成两个点,若这两个点都位于障碍物中,则检测它们的中点位置,若中点位于自由空间中则认为其处于窄通道中,通过大量的桥测试确定通道的形状以便对其补充采样[2],这种方法缺点是容易把障碍物的拐角和凹陷误认为是窄通道。PARK B提出了一种自适应环境的采样方法,首先把环境划分为大小不一的若干区域,不同区域间采样点数目一致,提取障碍物的边界点,根据边界信息移动采样点使其分布于窄通道中[3]。但这些研究往往对环境的全部状态空间进行采样,存在效率较低、难以增加有效采样点的问题。
1 针对窄通道问题改进的RRT算法
若要提高窄通道环境中的采样质量,需先识别出环境中的窄通道区域,本文参照文献[4]中的星形试验法,采用正交的双桥对采样点进行测试,从而使采样点分布在窄通道中,尽可能不陷入环境中的拐角和凹陷区域。
传统的单桥测试法需执行3次碰撞检测,双桥测试法需执行5次碰撞检测,而且窄通道区域在环境中的占比很小,如果直接对环境整体采样进行双桥测试,那么需要进行巨量的碰撞计算,才能识别出窄通道内的点。可以先将物体等比例缩小,用RRT算法查找出多条可行路径,把路径节点列入集合R中,在R中逐点对原物体进行碰撞检测,将无碰撞的点置入集合F中,再使用双桥法对F逐点进行测试,提取出窄通道内的节点置入集合Z中。
然后对原物体进行RRT路径规划,以一定概率偏向Z中的点和目标位置点采样,由于复杂环境中窄通道区域常和开阔区域并存,在算法执行中应将环境分为若干区域,设置步长随所在区域动态调整。可先大致划分区域,在不同区域设置初始步长,再计算该步长下,F中节点在向外拓展时与障碍物的碰撞概率,根据“开阔区域采用较大步长、窄通道附近区域采用较小步长,不同区域内F中节点在向外拓展时与障碍物的碰撞概率大致相同”的原则调整区域划分和步长。对于某些障碍物较多、边界复杂的区域,可设置步长为随机数,当物体在拓展新节点与障碍物发生碰撞时,以随机的小步长沿采样点方向生成新的节点,再进行碰撞检测,如此可增加障碍物附近的采样概率。
2 仿真分析
由于窄通道环境中RRT寻路耗时很长,限于硬件配置,本文设置了图1所示的简单窄通道环境进行仿真实验,长方形物体共有二维平面的移动加旋转3个自由度,碰撞检测算法采用基于分离轴检测的凸多面体碰撞算法[5]。
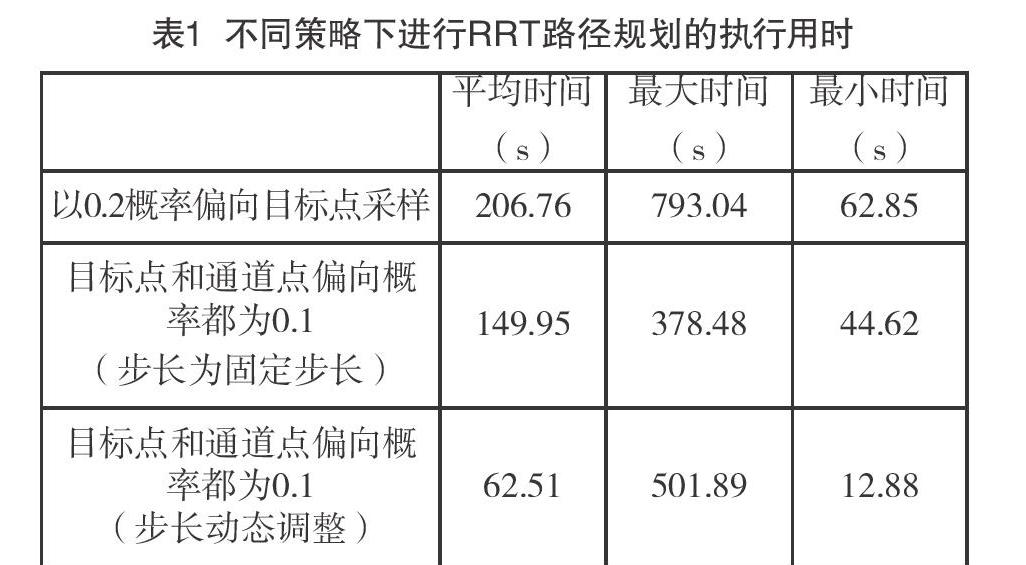
为对比RRT算法改进前后的性能,设定了不同的采样和步长调整策略,各自执行20次RRT算法,得到不同策略对应的执行用时(见表1)。
经典RRT算法只是偏向目标点采样,由于落在窄通道中的采样点很少,所以算法运行时间很长。改进后的RRT算法在识别出窄通道区域后,以一定概率偏向目标点和通道点采样,增加了窄通道内的采样密度,拓展节点时步长随区域调整,由于从开阔区域进入窄通道时对物体位姿约束很强,进入窄通道的过程往往耗时较长,该区域拓展节点发生碰撞时采用随机小步长再次尝试拓展,可以增加障碍物附近的采样,加速从开阔区域进入窄通道的过程。综合利用偏向窄通道的采样和动态步长调整策略,如表1所示,可使RRT算法的规划速度提高很多。
3 结语
针对有窄通道的环境路径规划速度过慢的问题,本文在应用RRT算法时进行了一些简单的改进,主要从识别窄通道和采样步长两方面,增加窄通道及附近区域的采样密度,仿真实验表明,改进后RRT算法的运行时间能缩小很多。但参数设置时还需大量人为调整,例如桥测试的线段长度、不同区域的采样步长值等等。希望未来能结合图像识别手段,自动设置相关参数,使之拥有更好的环境适应能力。
参考文献
[1] LAVALLE S. Rapidly-exploring random trees: a new tool for path planning[Z]. Research Report, 1998: 293-308.
[2] HSU D,JIANG T,REIF J,et al.The bridge test for sampling narrow passages with probabilistic roadmap planners[C]// Proc of IEEE International Conference on Robotics and Automation. New York: IEEE Press,2003: 4420-4426.
[3] PARK B,CHUNG W K. Adaptive node sampling method for probabilistic roadmap planners[C]/ / Proc of IEEE / RSJ International Conference on Intelligent Robots and Systems. Piscataway,NJ: IEEE Press,2009: 4399-4405.
[4] 钟建冬, 苏剑波. 基于概率路标的机器人狭窄通道路径规划[J]. 控制与决策, 2010, 25(12):1831-1836.
[5] 张应中, 范超, 罗晓芳. 凸多面体连续碰撞检测的运动轨迹分离轴算法[J]. 计算机辅助设计与图形学学报, 2013(1):7-14.
