挠性卫星的姿态控制算法

李浩东

摘 要：传统的卫星姿态控制算法未考虑到挠性部件对卫星本体姿态的影响（例如太阳能帆板的振动），为削弱這一不利影响，基于对卫星三轴姿态控制的研究，本文建立了卫星的数学模型并设计了一种考虑了挠性附件影响的PID控制系统。最后对PID控制器进行了MATLAB仿真，仿真结果表明，该PID控制系统对具有挠性附件影响的卫星的姿态有很好的姿态控制效果。

关键词：三轴卫星;挠性太阳能帆板;PID控制

自1957年10月4日，世界上第一颗人造地球卫星"斯普特尼克一号"发射升空后，世界卫星事业蓬勃发展，至今已发射了约6600颗人造地球卫星，应用十分广泛。随着卫星功能的日益强大，星载设备愈来愈多，卫星正不可避免的向大型化的方向发展。为了满足卫星的动力需求、更好的利用卫星，卫星上往往带有大型挠性太阳能帆板、挠性天线等挠性附件，属于一种挠性多体结构 [1]。

挠性附件具有结构大、质量轻、刚度柔的特点[2]，在卫星调整其姿态时，控制力在改变卫星的位置与姿态的同时还可能造成挠性附件振动、多体运动、液体晃动与内外扰动等影响，这些预期之外的作用会与卫星刚性本体的姿态控制发生耦合从而增大了卫星的转动惯量和受到的干扰力矩[3]。但是传统的刚性卫星在其三轴控制系统中未考虑到这样的问题，导致将带有挠性附件的卫星模化为刚体得到的控制律并不能正确控制卫星的动力学行为，并且，挠性体的振动速率与大范围刚体运动的速率呈正比例关系，当刚体运动速率大于等于某一值时，传统的动力学模型的误差较大，甚至完全错误[4]。下面介绍一个典型例子：

1958年，美国第一颗人造卫星“探险者一号”终于在“先锋号”的失败后成功发射，举国欢庆。殊不知，由于该卫星入轨自旋稳定后悬在星体外面的四根鞭状天线的弹性振动，造成系统的机械能部分转化为热能，最终卫星姿态失稳导致翻滚。之后，又有越来越多由于传统卫星控制率的缺陷致使卫星姿态控制失稳的事件发生[5]。

1999年，缪炳祺等在论文中详细介绍了挠性航天器动力学在二十世纪的发展史[6];2016年，张天赫在论文中详细阐述了对刚性卫星、带有挠性簇附件的卫星与挠性链附件的卫星的模块化建模问题并提出了对挠性附件动力学模型的修正[7]。目前，带有挠性附件的卫星的姿态动力学建模的问题已基本得到解决。其实，挠性振动等影响不仅是姿态控制的干扰，还是受控卫星特性的一部分[8]，而传统刚性卫星再设计控制率时忽略了这一特性，导致实际应用时出现了姿态误差，对于这样的姿态控制问题的研究，方兴未艾。并且我们知道，卫星的正常工作在满足轨道条件外往往还须要保持一个稳定的姿态，例如天文卫星的望远镜的朝向、资源侦察卫星的拍摄机和通信广播卫星的天线要对准地球等[9]。

为削弱挠性附件对卫星本体姿态的影响，本文通过引入对挠性太阳能帆板的有限元分析，对刚性三轴卫星的模型进行了修订，构建了一个具有挠性太阳能帆板物理影响的三轴卫星数字模型，同时设计了PID控制器，通过MATLAB仿真表明，该控制器对上述卫星模型进行了有效控制。

一、卫星模型与姿态控制流程

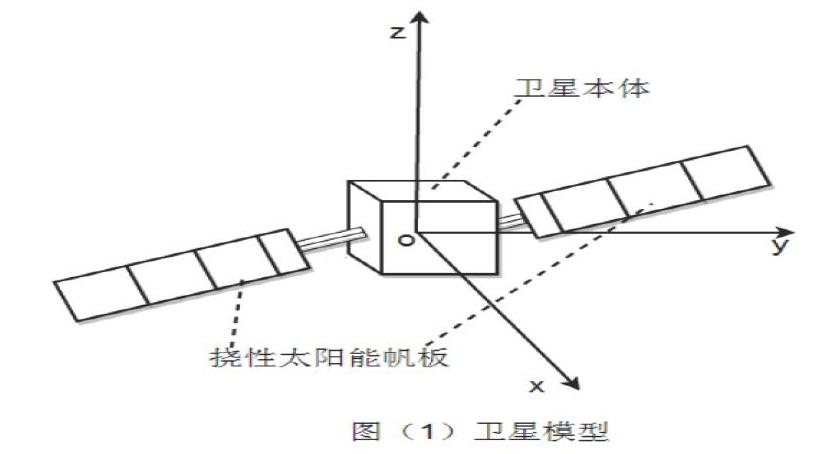
本文构建的卫星模型（图1）包括卫星本体、挠性太阳能帆板等。并且建立了卫星的本体坐标系（原点o与卫星的质心重合）。由于卫星绕x轴旋转为滚转运动;绕y轴旋转为俯仰运动;绕z轴旋转为偏航运动，故x轴为滚转轴;y轴为俯仰轴;z轴为偏航轴。

在建模、控制器设计与仿真时，本文把卫星的本体（不包括挠性太阳能帆板）模化为刚体。而实际中，卫星本体并不只是一个简单的刚体，还有、燃料、天线等挠性体，这些挠性体都会对卫星的姿态控制产生影响。

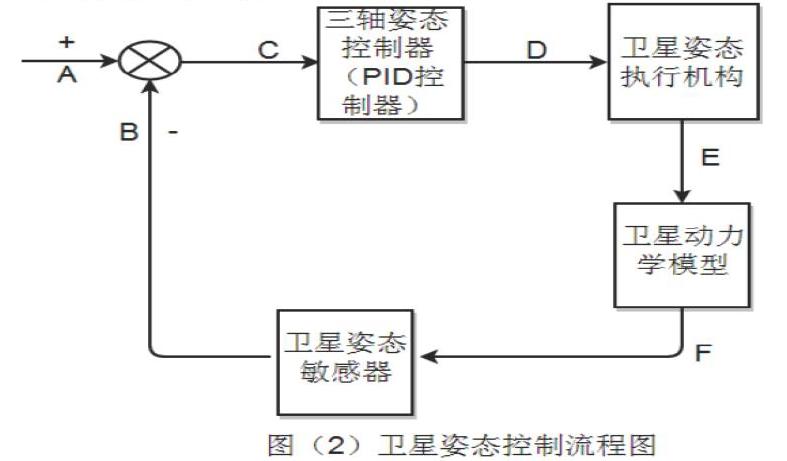
本文采用以三轴期望姿态为输入，实际姿态为反馈的卫星闭环控制模型。具体如图2所示：

图中：

A：三维矩阵形式的三轴姿态指令，即我们对卫星的期望姿态（给定值）。

B：敏感器（测量元件）测量到的卫星实际姿态数据（包含敏感器的误差）。

C：期望姿态与卫星敏感器敏感到的实际姿态间的姿态误差，可以表示为：C=A-B。

D：根据姿态误差，通过PID控制器的运算，得到的控制指令，作为姿态执行机构的输入。

E：执行机构输出的控制力矩，也是卫星动力学模型的输入。

F：卫星的真实姿态，是卫星敏感器的输入，也是闭环控制系统的被控量。

在输入三轴期望姿态指令后，PID控制器会根据期望值与敏感器得到的实际姿态间的误差姿态，计算输出三轴控制指令，三轴控制指令会输入姿态执行机构，并由执行机构产生相应方向的控制力矩。这些控制力矩是卫星动力学模型的输入，并由动力学模型得到卫星真实姿态。这时，卫星的姿态敏感器会对卫星姿态的各方面数据（如偏转角）进行精确的测量，随后得出卫星实际的姿态数据（包含测量误差）。将期望姿态与敏感器得到的实际姿态进行比较，计算出姿态误差并根据此误差进行新一轮的控制，直到预期姿态与实际姿态间的姿态误差满足一定的范围，达到期望的姿态。

二、卫星敏感器

在卫星的闭环控制流程中，卫星姿态敏感器肩负着测量卫星的真实姿态并得到三轴姿态数据的任务，即输入F（卫星的真实姿态）输出B（实际姿态数据）（图2），是至关重要的一环。本文列出并比较了几种常见的卫星姿态敏感器（表一）。

为了更好地敏感卫星的真实姿态，满足卫星对姿态敏感的要求，在同一个航天器上往往把多种敏感器进行组合，以综合不同敏感器的不同优点。本文也进行了组合： 以数字式太阳敏感器为主要的敏感装置，将激光谐振式陀螺仪作为备份。由于数字式太阳敏感器能够避免太阳能帆板等反射的太阳光干扰，而且功耗低、精度高、寿命长，故可以持续地对卫星的真实姿态进行准确测量，使误差在可控范围之内。但是，当卫星处在地球阴影区时，此敏感器无法接受到来自太阳的信号，无法工作，使闭环系统无法运行。然而，当这种情况发生时，我们将使用激光谐振式陀螺仪。该敏感器精度高、寿命长、重复性好、动态范围宽，也可以持续而准确地进行测量，并且很好的弥补了数字式太阳敏感器无法在地球阴影区工作的不足。所以，我们将数字太阳敏感器和激光陀螺仪进行组合。

三、卫星的执行机构

在闭环控制流程中，卫星的执行机构是卫星姿态控制力矩的具体执行者。在得到由PID控制器計算出的三轴指令后，执行机构会根据该指令输出控制力矩，对卫星姿态进行控制，让卫星姿态向给定值靠近。表二列出了几种执行机构并对他们进行了比较。

和卫星的姿态敏感器一样，为了追求更好的姿态控制效果，输出更准确的控制力矩以及更长的卫星在轮工作时间，在同一个航天器上往往有多个执行机构组合在一起。本文给出的组合是：以动量交换式执行机构中的动量轮为主要的执行装置，把喷气推进器作为备份。动量轮可以不断地从太阳电池获得能量，持续性很好，而且精度稳定度高、寿命长、轻而小、能耗低，在三轴方向上都安装上动量轮后，可以对卫星进行稳定而准确的姿态控制，性能优良。但它并不完美，因为在运行过程中，如果卫星受到强的干扰力矩，动量轮就容易达到饱和，这就要求必须有卸载装置辅助动量轮的工作，喷气推进器就扮演着这样的角色。这样一来，一般情况下的小范围扰动由动量轮负责，只有在遇到大范围扰动需要卸载或需要变轨时才用到喷气推进器，推进器的喷气周期大大延长，对氧气的消耗也大大减少。尽管推进器储备的气体有限，仍可以使用较长时间。所以这样组合比较合适。

四、有限元分析

有限元分析，是一个用数学方法模拟复杂的物理系统，求解复杂问题的工具。将一个复杂的结构近似成许多简单而又相互作用的单元，并通过对这些单元以及单元间节点的分析得到整个系统的模拟结果。由于实际上对许多工程问题的分析难以得到准确解，而有限元分析可以对复杂的系统进行高精度的模拟，所以得到了十分广泛的应用。ANSYS是一款功能强大的有限元分析软件，在此不做详细介绍。本文先用CATIA对卫星的尺寸、结构等参数进行了建模，随后将模型导入ANSYS并输入卫星的模型参数。ANSYS会模拟出卫星太阳能帆板的28阶模态，但由于其中的低阶振动不易衰竭影响较大，而高阶的很快衰竭，本文只考虑低阶振动。

五、卫星的动力学模型

随着卫星事业的不断发展，卫星上附带的挠性附件逐渐趋向复杂，系统中的自由度之间不可避免地存在着耦合作用。这种非线性的特点使得卫星动力学模型的求解非常麻烦，为了简化，本文在进行建模时认为自由度之间是正交的。

本文用牛顿-欧拉向量力学建模法并结合有限元分析进行卫星动力学建模。其它常用的方法还有凯恩（Kane）方程等。本文将卫星简化为一个带有挠性太阳能帆板的刚体，建立了如图3所示的坐标系。

图中：

O1-X1Y1Z1为卫星的惯性坐标系;

Ob-XbYbZb为卫星的本体坐标系，其原点是形变前卫星整体的质心;

Ok-XkYkZk为挠性太阳能帆板的坐标系。

Mt是卫星整体上n个质点中任意一个，由于本文将本体视作刚体，Mt处的卫星形变位移为零，其在惯性系的位置可以用向量表示。Mk是卫星挠性太阳能帆板上m个质点中任意一个，由于太阳能帆板是挠性体，Mk处存在形变位移，其位置可以用向量表示。Mt、Mk相对惯性系的线速度为

式中四个向量的物理意义如图3所示，表示卫星本体的绝对角速度。由于、一经确定即为常量，导数为零;卫星的形变位移在实际情况下是一个小量，可认为。故（1）（2）式又可以写成

由（3）（4）得到卫星的总动量为

式中MA是卫星整体的质量。由于Ob是形变前卫星整体的质心，Ob处整星的转动惯量为零，可得，则（5）式可以写为       由牛顿第二定律可得

式中是卫星受到的总主动力。由模态展开定理可得，其中（i=1，2L）是有限元分析得到的挠性附件的振型矩阵。是挠性附件的模态坐标，由于模态中的低阶振动不易衰竭影响较大，而高阶的很快衰竭影响较小，为简化运算，本文只考虑前三阶的振动。设A1为本体系到惯性系的转换矩阵，A2为挠性系到惯性系的转换矩阵，A3为挠性系到本体系的转换矩阵，则（7）式又可以写为

本文定义是挠性太阳能帆板在惯性坐标系中的平动耦合系数，是在挠性系中的平动耦合系数。可得卫星的平动方程为

由于实际中卫星既平动又转动，本文还推导了卫星的转动方程。设是卫星相对惯性坐标系的角动量，卫星受到的相对惯性坐标系的力矩，则有

约去卫星转动过程中的小量后，化简可得到

式中矩阵、（向量积），I是整星的转动惯量。本文定义是挠性太阳能帆板在惯性坐标系中的转动耦合系数，是在挠性系中的平动耦合系数。则卫星的转动方程为

式（10）与（13）即卫星的动力学方程。

在实际的操作中，还要进行卫星的运动学建模。这是由于卫星姿态敏感器所测得的三轴姿态角及角速度都是相对卫星本体坐标系而非惯性系的，所以需要运动学模型通过转换矩阵进行姿态的解算将姿态信息转换到惯性坐标系中，以满足姿态控制器的要求。

六、卫星控制器设计

在卫星姿态的控制器方面，本文采用PID控制算法，即比例（P）积分（I）微分（D）控制。其输入输出关系可由式（14）所示。式中是PID控制器的输出，是输入，是比例系数，、分别是积分系数、微分系数。

PID是一种应用广泛的控制算法，它简单易懂，实时性好;虽然它得不到精确的模型，但是精巧、复杂的设计结果往往并不比简单的PID更为优越，因为卫星的姿态控制需要实时性极好的控制器，若要得到精确的模型则需要一定时间。在PID的使用过程中，参数的整定是其中的核心步骤，当一个PID控制器完成安装后，参数的合适与否直接关系到系统的性能好坏。

PID参数整定的常见方法有经验法、响应曲线法、衰减曲线法、模糊控制、神经网络、遗传算法等[12]。本文采用响应曲线法进行PID参数整定，具体步骤如下：1、在MATLAB中断开闭环控制的反馈通道，并反复输入单位阶跃信号，进而得到响应曲线。2、曲线中可以得到时间常数、延时时间系数、输入输出的阶跃值和最大值最小值。3、利用相关公式得到PID的相关参数。本文拟定的参数是KP=0.8824;TI=160;TD=40，在此参数下，用MATLAB进行了卫星姿态角及角速度的仿真，如图4、图5所示。

本文模拟的控制时间为500s左右。卫星受到干扰后，卫星真实姿态角（俯仰角）最大误差为2°左右，期望值为0°;真实姿态角速度（俯仰角）的最大误差为0.84°/s左右，期望值为0°/s。由上图可以看出，在控制器的控制下，卫星的真实姿态角与真实姿态角速度都取得了明显的收敛效果，在450s后，卫星的姿态角与姿态角速度成功达到稳态，稳态精度分别是（1.3×10-3）°和（2.3×10-5）°/s，由此可见，本文设计的PID控制器对本文设计的卫星模型有良好的控制效果。

七、結语

本文的研究内容是削弱挠性附件对卫星本体姿态的影响。首先，本文简单介绍了：1、带有挠性附件的卫星模型2、闭环姿态控制流程3、常见的卫星姿态敏感器与执行机构。随后，本文针对挠性太阳能帆板进行了有限元分析，并构建了一个考虑到太阳能帆板挠性影响的动力学模型。最后，本文设计了一套PID控制器，并在拟定参数下用MATLAB进行了卫星姿态角及角速度的仿真，并取得了良好的姿态控制效果。由于本文考虑了挠性结构对卫星姿态的影响，故本文设计的姿态控制算法具有一定的实际应用价值。

参考文献

[1] 朱承元，杨涤，杨旭.大挠性多体卫星的自抗扰姿态控制系统设计[J].航天控制，2004， 22（6）：25-31.

[2] 吴云洁，李琛，马征.基于自抗扰滑模的三轴挠性卫星姿态控制[J].系统仿真学报， 2015， 27（8）：1831-1837.

[3] 刘刚，钟超，何益康，等.有大型挠性附件的卫星姿态线性鲁棒控制器设计研究[J].上海航天， 2017，34（2）：150-160.

[4] 蒋建平.大挠性多体结构卫星刚柔耦合动力学研究[D].国防科学技术大学研究生院， 国防科学技术大学， 2004.

[5] 马兴瑞等著.航天器动力学：若干问题进展及应用[M].科学出版社，2001.

[6] 缪炳祺， 曲广吉， 程道生.柔性航天器的动力学建模问题[J].中国空间科学技术，1999， V19（5）：35-40.

[7] 张天赫. 柔性航天器模块化动力学建模及模型修正[D].哈尔滨工业大学，2016.

[8] 胡乔木编.中国大百科全书：教育[M].中国大百科全书出版社，1985.

[9] 贾玉红等编.航空航天概论（第四版）[M].北京航空航天大学出版社，2017.

[10] 田菁， 吴美平，胡小平.三轴磁强计姿态确定[J].国防科技大学学报，2001， 23（5）：17-21.

[11] 胡玉琛.卫星姿控系统中的飞轮[J].国外导弹与宇航，1980（10）：23-28.

[12] 鹏程主编.自动控制原理（第二版）[M].高等教育出版社，2016.

[13] 黄宜庆.PID控制器参数整定及其应用研究[D].安徽理工大学，2009.