基于MABC-SVR的边坡安全系数预测模型
2019-04-04刘阳郝建斌魏兴梅
王 芬,刘阳,郝建斌,魏兴梅
(长安大学地质工程与测绘学院,陕西 西安 710054)
由于边坡所处的地质条件具有高度复杂性和非线性的特征,边坡变形的破坏机制也极其复杂,边坡的安全系数与各个不确定变量之间很难利用线性或非线性显式函数表达。因此,利用一种可靠的数学模型来反映具有高度非线性边坡破坏机制的方法成为众多学者研究的热点问题。遗传算法、蚁群算法、人工蜂群算法、粒子群算法和支持向量机等各种人工智能计算方法相继出现,以解决非线性的边坡工程问题。如吕文杰等[1]选择二进制编码的遗传算法搜索最危险滑裂面,尤其对于复杂边坡,搜索效果较好;徐飞等[2]采用蚁群优化算法对支持向量机参数进行了选择优化,提出了蚁群优化最小二乘支持向量机模型,并利用该模型进行了边坡稳定性分析;刘佳等[3]采用自适应智能搜索机制对人工蜂群算法进行了改进,以此来搜索最危险滑动面,求解边坡的最小安全系数,并通过实际工程算例验证了该方法的可靠性。
单一的智能算法不能准确地建立非线性程度较高的边坡极限状态方程,而支持向量机学习能力较强、灵活性更高,可在人工智能算法的基础上,搜索支持向量机的最优参数,从而获得更准确的预测模型。如马文涛[4]结合遗传算法和粒子群算法,对最小二乘支持向量机的最优参数进行搜索,结果表明遗传算法搜索效率较低,粒子群算法可达到快速全局优化的效果;李浩瑾等[5],Kang等[6]先后引入人工蜂群算法用于LSSVM 模型参数的优化,提高了模型的预测精度;Karaboga等[7]对不同算法进行了比较,验证了人工蜂群算法搜索的解更优、效率更高,其与蚁群算法、粒子群算法、遗传算法等相比,具有更好的优化性能。
但是原始人工蜂群算法求得的解多为局部最优解[8]。针对此问题,本文提出了一种改进的人工蜂群算法,该方法将原始人工蜂群算法的蜜源更新公式进行了改进,使迭代寻优过程更为高效,提高了全局搜索能力,进而运用改进的人工蜂群算法对支持向量机中的参数进行了优化,从而实现了对边坡安全系数的回归分析与预测。
1 支持向量机模型[9-11]
支持向量机(Support Vector Machine,SVM)作为一种高效的机器学习方法,已被广泛应用于处理分类、回归等问题。本文采用的支持向量机回归(SVR),是将原始数据x映射到高维特征空间得到φ(x),求解该空间中的线性回归问题。SVR遵循结构风险最小化原则,寻求训练样本的最小泛化误差上限,而不是预测误差,具有较好的推广能力。
对于非线性边坡,假设存在训练集{(xi,yi)|i=1,2,…,n},其中xi为D维输入向量,yi为输出目标,n为点的个数,则输入与输出之间的非线性关系可表示为
f(x)=wTφ(x)+b
(1)
式中:f(x)为预测值;w为权值向量;φ(x)为非线性映射函数;b为偏置或负阈值。
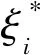
(2)
(3)
式中:C为惩罚因子,用以控制对错分样本的惩罚程度;ε为不敏感损失参数。
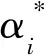
(4)
(5)

得回归函数为
(6)
若回归问题为非线性,则将输入向量映射到高维特征空间,转化为线性问题进行求解,这里引入内积核函数K(xi·x)=φ(xi)·φ(x),其中φ(xi)为输入变量xi在高维特征空间的映射。则非线性回归函数表达式为
(7)
式中:x为待测样本;xi为训练样本。
目前常用的核函数有3种,分别为多项式核函数、径向基核函数(RBF)和Sigmoid核函数。本文采用最适用的RBF核函数,其定义为
K(x,xi)=exp(-g‖x-xi‖2)
(8)
式中:g为核函数参数。
支持向量机中的惩罚因子C和核函数参数g对SVR性能起着重要作用[12]。因此,为了得到准确的回归结果,需寻找支持向量机中的最优参数,此过程可通过ABC算法迭代搜索实现。
2 人工蜂群算法
2.1 人工蜂群算法的原理[13-14]
人工蜂群算法(artificial bee colony algorithm,ABC算法)是一种受蜜蜂采蜜启发的种群算法。该算法中的四个组成要素包括蜜源、引领蜂、跟随蜂和侦查蜂。引领蜂的数量与跟随蜂的数量相等,并且等于蜜源的数量。当蜜源在一定迭代次数之内没有被改进时,引领蜂就会变成侦查蜂重新搜索蜜源,直至搜索到更优蜜源时,其角色又会重新变回引领蜂。实现ABC算法的具体步骤如下:
(1) 初始化种群,设定种群数量为NP,蜜源数量为FN=NP/2,最大搜索次数为Limit,最大循环次数为Maxcycle,蜜源维数D=2。
(2) 随机产生蜜源i的初始位置xij:
xij=xjmin+rand(0,1)(xjmax-xjmin)
(9)
引领蜂在蜜源i周围根据以下更新公式产生新蜜源vij:
vij=xij+θ(xij-xkj)
(10)
式中:i∈{1,2,…,FN},表示蜜源个数;j为[1,D]中的一个随机整数,表示引领蜂随机地选择一维进行搜索;xjmax为搜索空间上限;xjmin为搜索空间下限;k∈{1,2,…,FN},k≠i,表示在FN个蜜源中随机选择不同于i的蜜源;θ为[-1,1]之间的随机数,决定扰动幅度。
(3) 计算并比较vij和xij的适应度,若新蜜源适应度大于旧蜜源,则蜜源被更新,否则保留旧蜜源。
(4) 跟随蜂根据下面公式中的计算概率pi选择蜜源,接着与引领蜂相同的方式搜索更新蜜源:
(11)
式中:pi为跟随蜂选择蜜源i的概率;fiti为蜜源i的适应度,其计算公式如下:
(12)
其中,fi为蜜源i对应的解的函数值。
(5) 若蜜源i的迭代次数超过Limit仍未被改进,引领蜂便放弃该蜜源,进而转变为侦查蜂,重新搜索蜜源。
(6) 重复上述步骤(1)~(5),直至达到最大循环次数。
2.2 改进的人工蜂群(MABC)算法
原始人工蜂群算法虽搜索精度较高且鲁棒性较强,但易陷入局部最优解,蜜源更新公式(10)意为在所有蜜源周围寻找更高质量的解xbest,j,此过程较为繁琐且用时较长。本文先将原始蜜源的适应度进行排序,找出适应度最高的蜜源,然后在其周围搜索更优解,则蜜源的更新公式变为
vij=xbest,j+θ(xij-xkj)
(13)
为了测试改进的人工蜂群算法(简称MABC算法)的性能,选择了4个标准函数(两个单峰函数,即Sphere函数和Rosenbrock函数;两个多峰函数,即Griewank函数和Rastrigin函数)对两种算法[即原始人工蜂群算法(原始ABC算法)、改进的人工蜂群算法(MABC算法)]进行了仿真试验[8],通过测试搜索全局最小值能力来评价MABC算法的性能,其测试结果见图1至图4。

图1 Sphere函数的全局最小值收敛趋势Fig.1 Global minimum convergence trend of Sphere function

图2 Rosenbrock函数的全局最小值收敛趋势Fig.2 Global minimum convergence trend of Rosenbrock function

图3 Girewank函数的全局最小值收敛趋势Fig.3 Global minimum convergence trend of Girewank function

图4 Rastrigin函数的全局最小值收敛趋势Fig.4 Global minimum convergence trend of Rastrigin function
由图1和图2可见,本文提出的MABC算法全局性更好,在处理单峰函数时具备跳出局部最优解的能力;而原始ABC算法在处理Sphere和Rosenbrock函数时,分别在迭代次数为1 120和391时陷入局部最优。
由图3和图4可见,本文提出的MABC算法较原始ABC算法,在处理多峰函数时能在迭代次数较少的情况下搜索到全局最小值,收敛速度更快。
由此可见,通过改进蜜源更新公式,避免了蜜源搜索的随机性,能够使目标值更快地向全局最小值逼近。
3 基于MABC-SVR的边坡安全系数预测
3.1 边坡安全系数预测模型的建立
在边坡稳定性分析中,不确定变量用向量x=(x1,x2,…,xn)表示(其中变量x对应于边坡稳定的影响因素,n为影响因素的个数),边坡的安全系数用向量y=(y1,y2,…,yn)表示。对于具有高度非线性的边坡,可用支持向量机模型来描述边坡安全系数与影响因素之间的映射关系。由上述支持向量机理论可知,公式(7)为所要建立的预测模型,其中x为边坡稳定的影响因素,xi为第i个影响因素,αi和b可通过求解二次规划问题得到。
本文收集了文献[15]中80个边坡实例数据,将重度γ、黏聚力c、内摩擦角φ、边坡角φr、边坡高度H、孔隙水压力ru作为影响边坡稳定的6个不确定变量,将实例中的70个边坡数据作为训练集,用于建立边坡安全系数预测模型,10个边坡数据作为测试集,用于测试所建立的预测模型的精度。基于MABC-SVR的边坡安全系数预测模型建立的具体流程见图5。
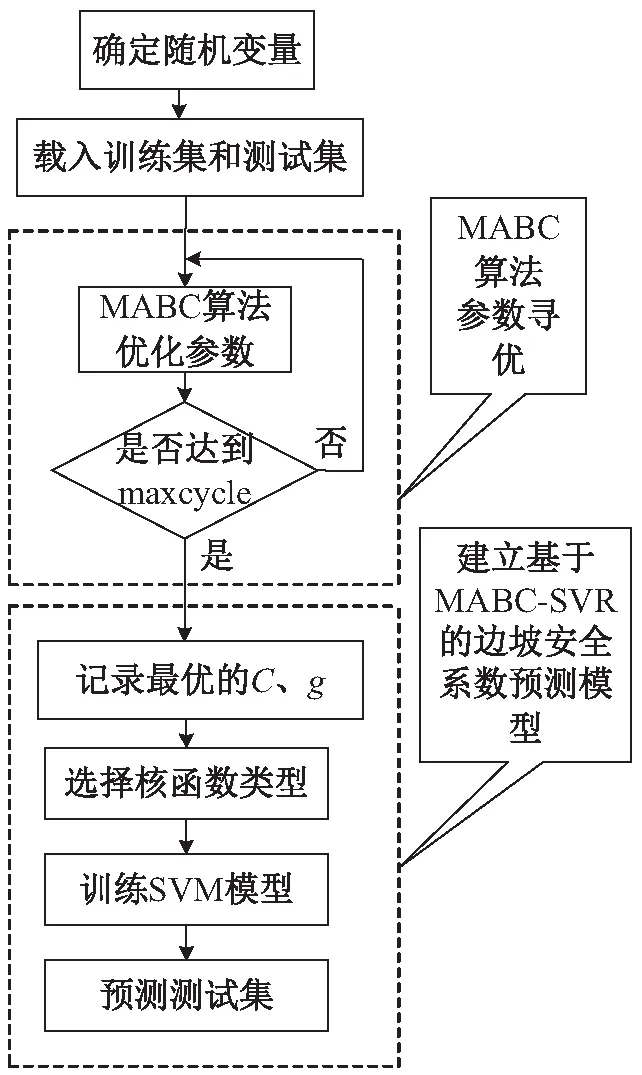
图5 基于MABC-SVR的边坡安全系数预测模型 建立的流程图Fig.5 Flow chart of slope safety factor prediction model based on MABC-SVR
3.2 参数优化结果及模型预测分析
在MATLAB软件中运行MABC算法,结果显示最优惩罚因子C为48.567 9,最优核函数g为7.116 2。利用最优参数建立SVR模型,该模型对训练集预测的回归系数r2=0.987 5,均方根误差RMSE=0.004 2,具体拟合情况见图6。采用所得训练模型对测试集预测的回归系数为r2=0.967 2,均方根误差RMSE=0.004 6,具体拟合情况见图7。

图6 边坡安全系数训练集实际值与预测值的 对比图Fig.6 Comparison of actual and predicted values of slope safety factor training set
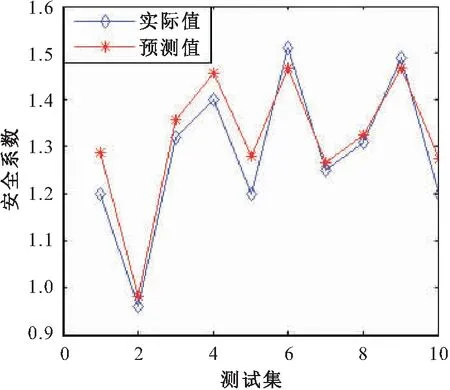
图7 边坡安全系数测试集实际值与预测值的 对比图Fig.7 Comparison of actual and predicted values of slope safety factor test set
由图6和图7可见,基于MABC-SVR所建立的预测模型能够较好地拟合样本点,即模型预测精度较高,误差较小。
为了较好地展现基于MABC-SVR的边坡安全系数预测模型的准确度,将基于MABC-SVR方法所得到的预测值与基于ABC-SVR方法和文献[15]方法的预测值进行了对比,其结果见表1和表2。
为了直观地分析对比预测结果,将表2中每种方法的最大相对误差做以标记(加粗字体),分析可知:MABC-SVR方法预测值最大相对误差为7.62%,较ABC-SVR方法和文献[15]方法误差更小,准确度更高。由此可见,基于MABC算法建立的支持向量机模型能够较准确地预测边坡的安全系数,更具有实际应用的价值。

表1 3种方法的预测值比较
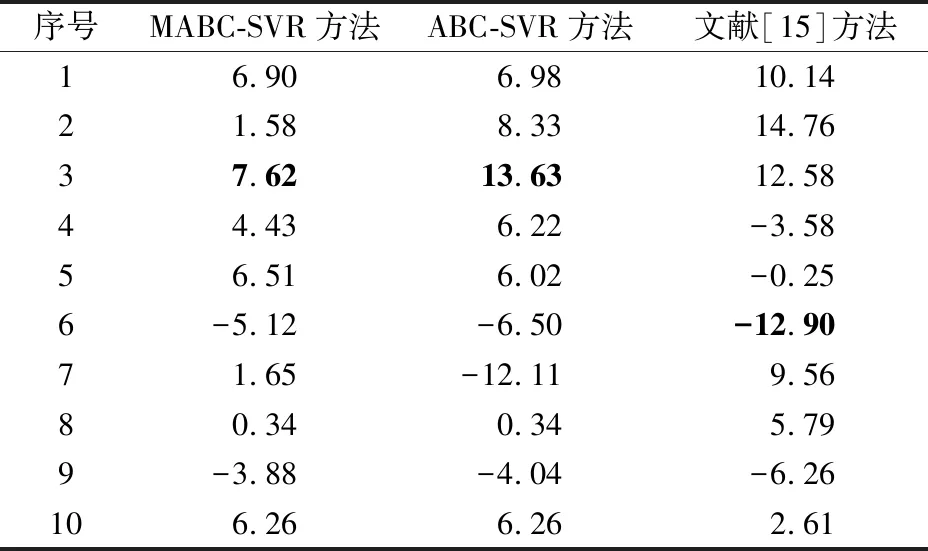
表2 3种方法的相对误差(%)比较
4 结 论
针对原始人工蜂群算法易陷入局部最优解、收敛慢等缺点,提出了一种改进的人工蜂群(MABC)算法,利用该算法搜索最优参数,并结合支持向量机建立了边坡安全系数预测模型。该改进的人工蜂群算法主要对原始人工蜂群算法的蜜源更新公式进行了改进,经测试表明该改进算法更具有全局性,且收敛速度相对提高。经边坡实例分析表明:利用MABC-SVR方法可快速建立边坡安全系数的预测模型,对比预测值与实际值,其回归系数高于0.95,最大相对误差不超过8%,预测结果的准确度较高。
