基于FEFLOW的岸坡地下水三维渗流场模拟研究
2019-04-04李庆伟晏鄂川崔学杰
李庆伟,晏鄂川,杨 广,崔学杰
(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.中交第二航务工程勘查设计院有限公司,湖北 武汉 430060)
三峡库水位的周期性波动引起岸坡内地下水渗流场不断地发生相应的变化,使得坡体与水的相互作用在很大程度上得以加强,导致岸坡稳定性的改变,甚至可能引发岸坡的局部或整体变形破坏。国内外许多学者对岸坡地下水渗流特征进行了一系列研究,取得了丰硕的科研成果。如Sevaldson[1]、Henkel[2]、Liu[3]和Wang等[4]对库水位升降作用下,岸坡地下水渗流场和失稳机理进行了相关研究,认为水是导致坡体变形破坏的主控因素;Szabo等[5]利用有限差分模型,模拟了瞬时水流的非稳定渗流;荣冠等[6]在研究降雨入渗机理和模拟方法的基础上,编写了非饱和渗流程序SUSC,并模拟了某边坡降雨过程中地下水渗流场的变化;谢瑾荣等[7]基于软岩边坡非饱和渗流-应力计算原理,将渗流与软化相结合,采用间接耦合法分析软岩边坡的降雨入渗,建立了软岩边坡渗流效应的分析方法;杨广等[8]利用数值模拟方法研究了地下水渗流和岸坡的稳定性,认为岸坡不同位置和高程处地形的改变因地表水力特征的差异而有所不同;还有一些学者也进行了大量的相关研究[9-12]。但由于不同库岸段工程地质条件的差异,部分特殊岸坡地下水的渗流特征仍没有得到合理的解释。
基于以上认识,本文在三峡水库蓄水条件下,通过构建涉水岸坡的渗流模型,基于FEFLOW软件对岸坡地下水渗流场的变化情况进行了三维数值模拟研究,从而揭示水库正常运行期间库岸内部地下水渗流场的发展动向与变化趋势。
1 涉水岸坡工程地质概况
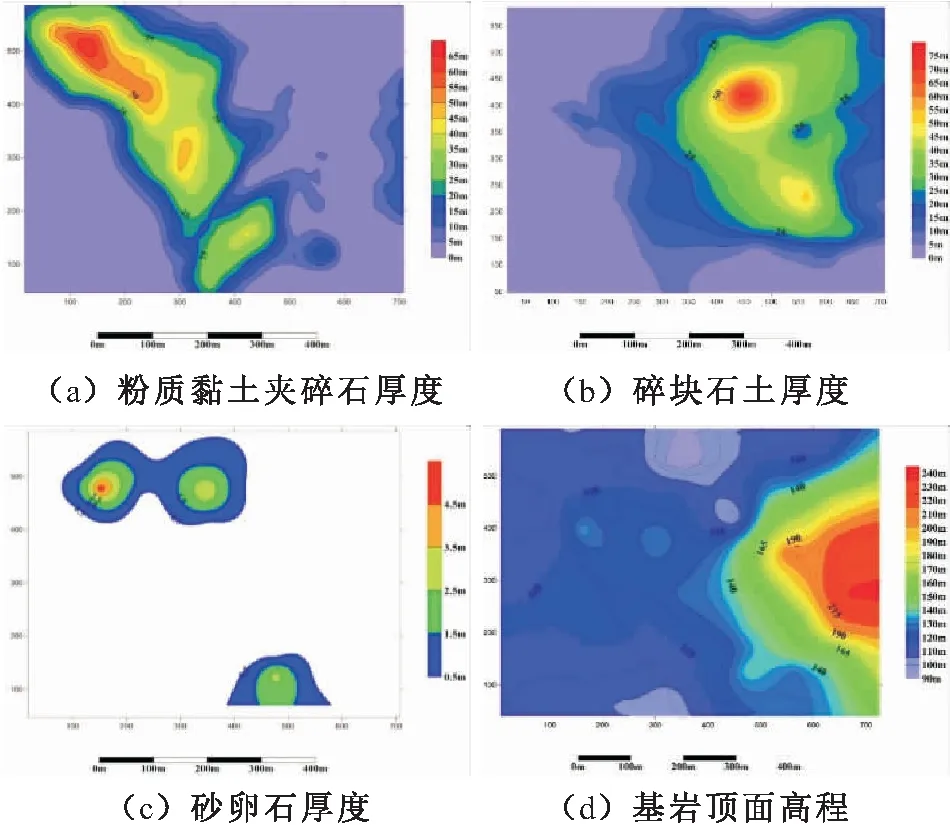
图1 研究区地层分布图Fig.1 Formation distribution map
研究区位于重庆巫山县长江与大宁河交汇处江东咀地区,平面上呈“舌状”,为长江与大宁河的阶地,属于构造侵蚀、剥蚀河谷地貌。据现场调查和钻孔揭露,研究区内地层主要为第四系人工填土层、冲洪积层、崩坡积层和三叠系下统嘉陵江组第四段灰岩地层。第四系覆盖物以粉质黏土夹碎石、碎块石土、砂卵石层为主。其中,粉质黏土夹碎石在研究区分布较为广泛[见图1(a)],主要位于大和尚包、小和尚包及小狗架子沟附近,厚度分布不均匀,最厚可达70 m;碎块石土主要分布在红梁子沟—小狗架子沟以北,厚度一般为50~60 m,局部地区可达到80 m[见图1(b)];红梁子沟—小狗架子沟以南的部分钻孔及以北的钻孔SXZK10中揭露到砂卵石夹碎石层[图1(c)],砂卵石层一般直接覆盖在基岩之上,上覆碎块石土或粉质黏土夹碎石,其厚度变化较大,最厚处达5.2 m。基岩以三叠系下统嘉陵江组第四段灰岩为主,主要在研究区东北部出露地表,即神女庙周边地区,基岩的埋深变化较大,基岩面陡峭[见图1(d)],基岩顶面高程为90~240 m,但在红梁子沟附近基岩顶面高程急剧降低(90~100 m),推测是岩溶塌陷造成;此外,基岩在神女庙附近埋深较浅,基岩顶面高程为210~240 m,覆盖物厚度为10~20 m。研究区内及其附近无断层通过。
2 计算原理与方法
2.1 计算原理
当不考虑水的密度的变化条件下,在孔隙介质中地下水在三维空间的流动可以用下面的偏微分方程来表示[13]:
(1)
式中:Kxx、Kyy、Kzz分别为x、y、z主方向的渗透系数;ω为源汇项,包括蒸发、降雨入渗补给、井的抽水量和泉的排泄量等;μs为储水率;H0为初始地下水水位;Ω为地下水渗流区域;H1为河流水位;S1为第一类边界(给定水位边界条件);S2为第二类边界(给定流量边界条件);q(x,y,z,t)表示在边界不同位置上不同时间的流量。
公式(1)构成了对于一个实际问题地下水流动的定解问题,可采用数值计算方法进行求解,如有限差分法、有限单元法等,求解结果即为地下水水位的分布值。
2.2 计算方法
目前地下水渗流数值计算主要采用有限单元法和有限差分法。其中,美国地质调查局在20世纪80年代开发的MODFLOW(Modular three-dimensional finite difference groundwater flow model)为有限差分法的典型代表[14],而本文研究所使用的FEFLOW(Finite Element subsurface FLOW system)则是基于有限元法的地下水数值模拟软件。该软件是一种求解偏微分方程定解问题的有效数值方法,成功地解决了众多领域的许多计算问题[15-17],如地下水流动、水动力弥散问题等。
3 数值模拟方案设计
在现场调查的基础上,结合研究区的地质资料,建立了水库正常运行条件下岸坡地下水运动的三维地质模型,并利用数值计算方法对不同工况下岸坡地下水三维渗流场进行模拟。依据三峡工程正常运行期水库的调度特征(见图2),本次数值模拟研究采用如下4种工况:①145 m低库水位(即工况Ⅱ);②145 m库水位上升至175 m(即工况Ⅱ);③175 m高库水位(即工况Ⅲ);④175 m库水位下降至145 m(即工况Ⅳ)。为了简化模拟过程,每月按30 d计,对较小的库水位波动忽略不计,以该期间的特征库水位为准,设计的涉水岸坡地下水三维渗流场数值模拟具体方案,见表1。

图2 三峡工程正常运行期水库调度图Fig.2 Reservoir operation chart of Three Gorges Project during normal operation period注:(1)为防破坏线;(2)为限制供水线;(Ⅰ)为防洪区;(Ⅱ)为装机预想出力区;(Ⅲ)为保证出力区;(Ⅳ)为降低出力区(资料来源于《三峡库区地质灾害防治工程地质勘查技术要求》)

工况时间库水位/m历时/dⅠ6月中旬至9月145105Ⅱ10月145~17530Ⅲ11月至次年4月末175180Ⅳ5月至6月中旬175~14545
3.1 数值模型的构建
数值计算范围根据江东咀库岸段研究范围和库水位变化特征综合确定。根据三峡库区的库水位调度特征,本次岸坡地下水三维渗流场的数值模拟库水位变动范围设定为145~175 m,选取130 m等高线在水平面上的投影作为模型边界,顶面高程则依据实际地形确定。为了便于建模,将地形整体顺时针旋转了43°,模型在平面上的投影近似于一个梯形,见图3。数值计算模型长约726 m,宽约592 m,平面面积约为0.42 km2,地表高程范围为130~268 m,相对高差为138 m。

图3 数值模型范围Fig.3 Domain of numerical model注:zk22〇为钻孔编号及位置
研究区内土层的分布情况较为复杂,且存在尖灭情况,完全再现地质结构是很难实现的。另外,研究区粉质黏土夹碎石与碎块石土渗透系数的差异远小于库水位的日升降幅度,因此在进行岸坡地下水三维渗流场数值模拟时可将其视为同一层;砂卵石层分布范围小且厚度薄,对岸坡地下水渗流场的影响十分有限,因此本次模拟忽略砂卵石层,将研究区地层简化为上覆第四系土层和下伏基岩的结构。
建立的舌状涉水岸坡三维渗流模型,见图4。该模型分为两层,即第四系覆盖层和基岩。地表使用实测地形图生成,其他各层则根据钻孔资料并结合surfer平台,采用克里金插值法生成初步模型,再进行微调生成。模型共包括节点14 820个,单元18 790个。研究区单元的划分不均一,在145~175 m高程范围内进行了网格加密。

图4 舌状涉水岸坡三维渗流模型Fig.4 Three-dimensional seepage numerical model of groundwater in the tongue-shaped bank slope
3.2 边界条件、参数选取和初始条件
3.2.1 边界条件
模型的边界条件是指确定模型中各单元的水头性质,用以判定是定水头单元、变水头单元或是无效水头单元。江东咀库岸段斜坡整体呈舌状,处于三面涉水的环境中,仅向东北侧延伸,由于库水位周期性升降,涨落高差达30 m,故认为模型东北侧是变水头较符合实际情况;模型东侧边界钻孔基本无水,库水位的变化对其影响不大,可作为不透水边界;其他三面的变水头边界则视表1中的工况予以确定。
3.2.2 参数选取
本次调查期间,库区处于降水期,但库水位保持在166 m以上,钻孔显示地下水水位基本与其持平。随着库水位的下降,部分单元将变为干单元,在这个过程中,利用三维渗流模型计算地下水在这些单元的变化时所用的参数也由储水系数S转变为给水度μ,因此三维渗流模型所涉及的计算参数包括渗透系数K(水平方向Kx、Ky,垂直方向Kz)、给水度μ和储水系数S。限于所采用的手段和可用的资料,本文将岩体近似作为一种连续、均质的介质。
经现场钻孔抽水和注水试验,粉质黏土夹碎石和碎块石土的渗透系数分别为2.64×10-6m/s(即0.228 m/d)、3.63×10-6m/s(即0.314 m/d),第四系覆盖层的渗透系数综合取值为0.3 m/d;基岩岩体裂隙发育,本身较破碎,但普遍存在泥质、钙质填充、胶结的现象,其渗透性较弱,可将其视为隔水层,渗透系数取值为10-5m/d。给水度μ和储水系数S按经验取值,具体取值详见表2。

表2 三维渗流模型的计算参数
3.2.3 初始条件
初始条件即初始水位的确定。目前共有三种方法可以用来确定库区地下水水位的分布情况:一是根据钻孔中地下水水位的埋深资料,利用插值方法或趋势面分析得到;二是先利用类比方法确定该地区的水力坡度,利用该水力坡度和现今的库水位推算出各单元的地下水水位埋深;三是对模型进行稳定流模拟,利用模拟的结果作为模型的初始水位。由于野外钻探工作在库区降水位期间进行,且钻孔水位随库水位变化明显,实时记录存在误差,无法直接用来确定初始水位,而类比方法精度较差,故本次模拟采用了第三种方法,即将第一个水文年的稳态模拟结果作为下一个水文年的初始水位。
4 模拟结果与分析
岸坡地下水三维渗流场数值模拟分两个水文年进行,第一个水文年的模拟结果用以确定初始水位,重点分析在第二个水文年中舌状涉水岸坡地下水三维渗流场特征及其变化规律。
第一个水文年模拟三峡库区首次蓄水至175 m库水位的工况:首先,库水位在30 d内由145 m上升至175 m,升幅30 m,平均上升速度为1 m/d;水库蓄水至175 m后,开始进入正常运行阶段;然后,经过180 d(11月初至次年4月末)后,在汛期前大幅度缓慢下降,即在大约45 d(每年5月初至6月中旬)内库水位从175 m降至防洪限制水位145 m,降幅30 m,平均下降速度约为0.67 m/d;最后,保持145 m低库水位运行105 d,地下水水位分布见图5(a),并且该水位将作为第二个水文年的初始水位。
第二个水文年模拟水库正常运行期间,库水位对地下水渗流场的影响,其中库水位变化与第一个水文年相同,其模拟结果见图5至图8。
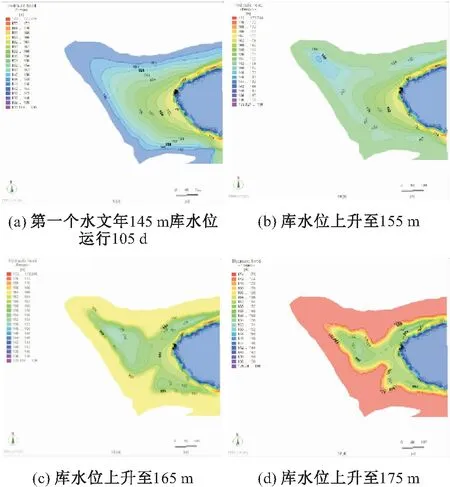
图5 工况Ⅱ下岸坡地下水水位分布图Fig.5 Distribution map of groundwater level of the bank slope in working condition Ⅱ
由图5可见,在库水位由145 m上升至175 m期间,舌状涉水岸坡内地下水水位变化有很大的区别:在大和尚包以西范围内地下水水位值的变化最快,当库水位上升至175 m,地下水水位几乎同步上升至175 m,这主要是由于该处地形狭窄,渗流路径比较短,另外该区域内地表高程(174~176 m)与库水位十分接近;大和尚包以东至红梁子沟一带,地下水水位变化也相对较快,同时在大、小和尚包一带出现类似“地下水漏斗”的渗流特征,即中部水位低而周边水位高,175 m地下水水位等值线平面范围逐渐向内扩展;在红梁子沟—小狗架子沟东侧区域,由于相对远离库水且靠近基岩面,地下水水位的变化较缓慢。
由图6可见,当水库保持175 m高库水位运行时,舌状涉水岸坡地下水水位逐渐上升。在运行的前90 d内,地下水水位的变化较明显;而90 d后,地下水水位等值线的空间范围和数值基本都不再发生变化,除坟院子和神女庙附近地下水水位依然保持145 m左右,其余各处地下水水位均达到175 m。分析原因认为:红梁子沟—小狗架子沟以西,基岩埋深较深,第四系覆盖物较厚,且地形较狭窄,渗流路径较短,地表高程普遍低于190 m,地下水可以很快与库水产生联系,并达到平衡;而红梁子沟—小狗架子沟以东则刚好相反,不仅海拔高,而且地形宽阔,导致渗流路径变长,加之作为相对隔水层的基岩埋深浅且基岩面陡峭,因此当保持175 m高库水位运行180 d时,高程175 m处基岩面附近的第四系覆盖层部分可以达到175 m的地下水水位,而基岩内仍然保持稳定流模拟的145 m地下水水位,其变化梯度和范围在理论上存在,但限于数值模拟的精度,很难在图形中予以区别。

图6 工况Ⅲ下岸坡地下水水位分布图Fig.6 Distribution map of groundwater level of the bank slope in working condition Ⅲ
由图7可见,库水位由175 m下降至145 m,舌状涉水岸坡内地下水水位变化与库水位上升过程有所不同。库水位下降过程中,地下水水位值的变化慢慢减缓,小和尚包至坟院子一带在库水位下降至145 m过程中,始终保持170 m以上的地下水水位,这主要是由于地形坡度导致渗流路径的变长。
由图8可见,当水库保持145 m低库水位运行时,舌状涉水岸坡地下水水位逐渐下降,地下水水位等值线整体上表现为“西疏东密”,即地下水水位在西部区域变化最快,往东逐渐减缓;保持145 m低库水位运行105 d后,岸坡内地下水渗流场仍未达到稳态,地下水仍然在向长江和大宁河排泄,但新一轮的库水位上升即将开始,地下水渗流场将重新进行调整。

图7 工况Ⅳ下岸坡地下水水位分布图Fig.7 Distribution map of groundwater level of the bank slope in working condition Ⅳ

图8 工况Ⅰ下岸坡地下水水位分布图Fig.8 Distribution map of groundwater level of the bank slope in working conditionⅠ
通过对比分析图5至图8可知,舌状涉水岸坡地下水三维渗流场还具有以下特征:
(1) 地下水水位分布与地形有极大的相似性,沿舌状岸坡山脊线呈对称分布,且地下水水位随地形的起伏而产生相应的变化,但变化的幅度略小于地形坡度。地下水水位等值线整体上表现为“西疏东密”,主要受地形坡度的控制,与基岩(相对隔水层)的埋深也有一定的关系。
(2) 地下水水位上升和下降的速度明显滞后于库水位的变化。这主要是由于库水位的日变化幅度远大于岸坡的入渗量,即岩土体的渗透系数太小。另外,通过对比分析图5(a)和图8(f)可知,相同时间节点,第二个水文年的地下水水位略高于第一个水文年的地下水水位,证明地下水在坡体内有一定的“滞留积累”效应,部分区域地下水水位在水库保持145 m低库水位运行105 d后仍然保持在170 m以上。
(3) 库水位的变化对红梁子沟—小狗架子沟以西区域地下水渗流场的影响较大,地下水水位等值线的变化更为明显,而东侧区域地下水渗流场则较为稳定。
本次数值模拟研究能基本反映在库水调动的条件下,该舌状涉水岸坡体内地下水三维渗流场的变化特征。但也存在些许误差,如东部区域基岩范围内一直保持着稳定流模拟的145 m地下水水位,地下水水位的变化梯度和范围难以看出。这种误差产生的原因包括两个方面:①建模误差。建模过程中,简化了岸坡的物质组成结构,且限于计算机硬件的限制,网格的划分也不能太密,因此无法保证岸坡的三维数值模型与其真实的地质结构保持完全一致;②参数误差。渗透系数采用了野外抽水试验测得的参数,而给水度和贮水系数无法在野外测得,则采用了经验系数,存在一定的误差。
5 结 论
本文运用有限元方法,通过三维数值模拟软件FEFLOW,对简化条件下的涉水岸坡地下水渗流场进行了三维数值模拟研究,并得出了以下结论:
(1) 岸坡地下水水位变化与库水位呈正相关性,表现为地下水水位随库水位的升高而升高,且这种变化具有明显的“滞后效应”,存在地下水渗流中的“漏斗”现象。
(2) 岸坡地下水水位分布与地形密切相关,红梁子沟—小狗架子沟以西区域地下水渗流场受库水的影响较大,而东侧区域地下水渗流场则较为稳定,且坡体内的地下水水位沿舌状涉水岸坡山脊线呈对称分布。在地形狭窄的区域,由于渗流路径短且紧临库水,地下水水位变化较快,表现为“西疏东密”的分布特征;库水位下降阶段,地形坡度的存在导致渗流路径变长,因此岸坡地下水水位的变化也比库水位上升阶段要缓慢。
(3) 岸坡地下水水位的分布与基岩面的位置(相对隔水层)有关。该舌状涉水岸坡东部区域基岩埋深浅且基岩面陡峭,其附近的覆盖层区域地下水水位等值线分布密集,而基岩内部由于相对隔水,其库水位值一直保持初始稳态分析的145 m低库水位。
