变工况运行的制冷压缩机功率消耗的定量关系式研究

王晓燕，焦卫东，朱利民

（浙江师范大学工学院，浙江金华321004）

1 引言

压缩机是蒸汽压缩式制冷系统的核心部件及动力源，在实际运行时，由于压缩机受高温高压、油气混合等多变环境的影响，使得对其变工况运行下的热力性能的研究显得尤为困难和复杂。压缩机的热力性能除受自身结构和工艺的影响外，还受其运行工况的影响，且各因素间存在交错复杂的关系，其热力性能参数很难用具体的数学模型来精确表示[1]。为便于工程应用，根据以往经验，在建立计算模型时常常需要根据影响压缩机热力性能的主次关系，对其相应参数进行一些必要的处理，处理的结果势必会对其计算结果的准确性产生影响。

在压缩机热力性能研究方面，众多学者的研究主要集中在以下两个方面：一是通过实验获得变工况条件下各种实验数据，通过拟合获取制冷压缩机热力性能与各主要热力学参数之间的关系式[2-5]；另一方面是利用各种控制算法进行数值模拟计算得出新的热力计算模型[6-9]。本文在前人研究基础上，依据热工学理论，对其机理模型进行工程处理，构建压缩机功耗随各主要热力学参数间的定量关系式。

2 压缩机功耗定量关系式研究

图1 实际循环的等功简图

压缩机的指示功率可利用热力过程方程式计算，也可参照文献[10]中的公式进行计算。文章在推导功耗定量关系式时一方面为了保证计算精度，使其计算结果更逼近压缩机实际工作过程，同时又要满足方便工程计算需求、采用等功法[10]对实际示功图作必要的简化，如图1所示。压缩机实际吸、排气过程线分别用平均吸气压力损失Δpsm线4′-1′和平均的排气压力损失Δpdm线2′-3′来代替；再分别从1′、3′点作1′-2′和3′-4′等功多变指数过程线代替原来的多变指数过程。这样，循环指示功Wi为

假设m=n′，上式变成

若近似认为

式中 ε——压缩比

λv、λp——分别为容积系数和压力系数

δs、δd——吸气过程与排气过程中平均相对压力损失

Z1′、Z2′——1′、2′点的压缩因子

则式（2）可化为

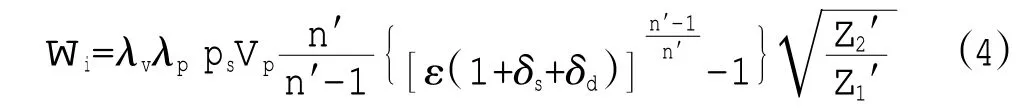
式中 Vp——气缸容积

指示功率（单位kW）为

式中 i——气缸个数

D——气缸直径

n——气缸转速

在压缩机设计阶段计算指示功率通常采用此方法，由于在推导该公式时也进行了一定的假设，故采用此方法计算得出的结果与实际值之间还存在一定出入。

Wi的精确计算式为式（1）

为了分清楚各影响因素对计算结果的影响，更准确的分析指示功率的与各参数之间的关系，本文进行了进一步分析。为方便工程应用计算，不考虑实际气体可压缩性时，则

综合公式（3）和公式（7）可知，在压缩机结构一定的前提下，当进、排气压力ps、pd一定时，循环指示功Wi仅与m、n′、δs、δd等参数有关。

根据文献[11]知，Wi随着等功多变膨胀指数m或等功多变压缩指数n′的增大而增大；随着δd较少或δs增大而减小。从其文献[11]的计算结果看，其中以n′对Wi的影响最大，δd影响最小。故在压缩机的设计与计算时，n′的选取非常重要，m的选取有时会有较大的影响，也要尽可能选取合适值；δs和δd对Wi的影响相对较小，δd影响尤其小，因而可采用简单近似的方法来确定δs和δd的值。本文拟采用经验值，取δs=0.06，δd=0.08[10]。

根据某生产厂家提供的NS1112Y压缩机工作过程的示功图，采用数值分析，通过迭代计算出该型号等功多变压缩和膨胀指数分别为n′=1.15和m=1.14。根据上述分析，因压缩指数n′与膨胀指数m相差不大，且等功多变压缩指数n′取值较重要，为简化计算，本文令m=n′≈1.15。指示功率Pi（单位W）可简化为

根据文献[10]知

且该文献指出，Δpd3=（0.10~0.15）pd，Δps1=（0.05~0.07）ps，本文取

轴功率是指示功率与摩擦功率之和，即

在压缩机转速不变的前提下，摩擦功率与压缩机运行工况无关。因此，对摩擦功率pm的计算，可采用把压缩机在空载下（压缩机的温度状态尽量维持不变）所测得的轴功率作为压缩机在各种工况下的摩擦功率来看待，也可利用平均摩擦压力pm这个参数来计算其大小。Pm的物理意义是压缩机单位气缸容积在一循环中所消耗的摩擦功。因此，摩擦功率Pm（单位为kW）可以用下述关系式表示：

对 于 顺 流 式 氟 利 昂 机，pm=（0.30～0.50）×105Pa[10]，本文取pm=0.4×105Pa。

对于往复式全封闭压缩机，因电动机与压缩机公用一根轴，所以可以忽略传动效率。因此压缩机功耗等于轴功率，即为

3 实验验证

3.1 实验系统及工况设定

为验证公式的正确性与可行性，作者设计了相应的实验进行验证。实验装置如图2所示，测试系统采用“第二制冷剂量热器法”进行性能试验，进口处压力可由设置在量热器和冷凝器处的第二制冷剂的温度进行调节，过冷温度和环境温度都分别为32.2℃。所测试压缩机型号为NS1112Y型，气缸容积为8.1 cm3，转速为2930 r/min，制冷剂为R600a。设计本实验的目的是为检验本文推导的机理模型的正确性，研究制冷压缩机功耗与其主要热力学参数吸、排气压力之间的定量关系。实验以压缩机吸、排气压力为自变量，并在实验标准工况周围作大幅度变化。吸气压力从0.03743 MPa变化至0.08742 MPa，排气压力从0.5613 MPa变化至0.7713 MPa。

3.2 实验数据与计算结果比较

计算值可根据公式（11）计算出不同工况条件下压缩机的功耗，排气压力pd分别为0.7713 MPa、0.7113 MPa、0.6613 MPa、0.6113 MPa和0.5613 MPa下，ps分 别 为0.03743 MPa、0.04243 MPa、0.04743 MPa、0.05243 MPa、0.05743 MPa、0.06243 MPa、0.06743 MPa、0.07243 MPa、0.07743 MPa、0.08243 MPa、0.08743 MPa、0.09243 MPa时的压缩机功耗计算值和实验值，其比较结果如图3~7所示。

图2 实验装置结构示意图

图3 p d=0.7713 MPa下的功耗值比较

图4 p d=0.7113 MPa下的功耗值比较

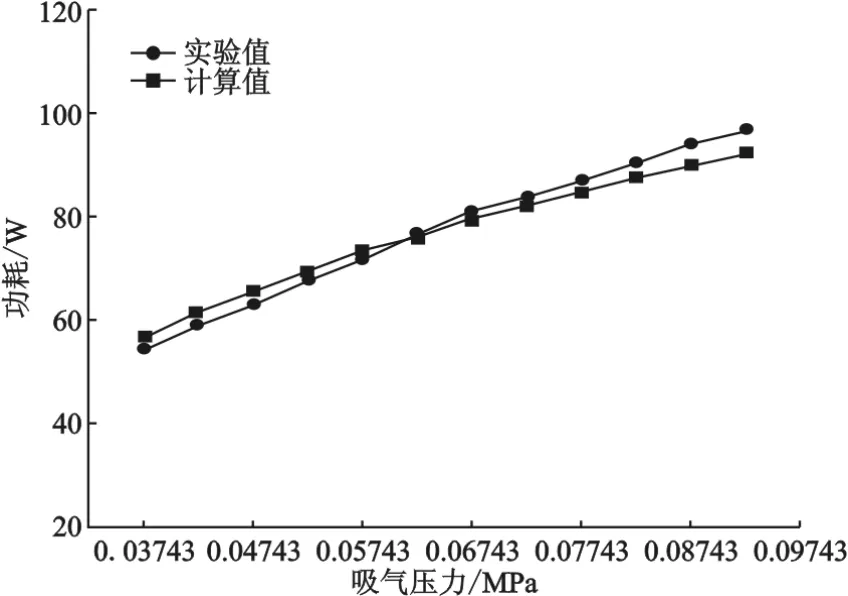
图5 p d=0.6613 MPa下的功耗值比较

图6 p d=0.6113 MPa下的功耗值比较

从图中数据显示，制冷压缩机功耗的理论计算值与实验值吻合较好，二者的最大相对误差为4.64%，最小误差0%，平均误差2.75%。该数据表明，本文推导的压缩机功耗计算式计算结果可靠，能够满足工程设计计算要求。

图7 p d=0.5613 MPa下的功耗值比较

3.3 产生误差的原因分析

上述计算结果与实验结果虽吻合度较高，但两者之间还存在一定的误差。究其造成误差的主要原因有：

（1）实验误差：测量装置中采用的各种检测仪表如数据采集仪、压力表、压力传感器、温度表等因本身精度不够会造成一定的实验误差；在实验测试过程中，由于采用“第二量热器法”进行实验，输入数据调节的迟滞性造成测试工况的不稳定会引起输入功率记录有偏差；因为环境温度、湿度、气压等的变化不可避免的使系统稳态产生波动；另外由于操作不当等也会产生误差。

（2）机理分析模型误差：产生误差的一个重要原因是考虑的影响因素不全面，建立的模型不够完善。在构建模型时，需要考虑模型的可解性同时又要兼顾模型的实用性，常常需要进行一些假设与简化；本文在构建模型时忽略了对计算结果影响比较小的一些因素，比如忽略了实际气体的可压缩机性、制冷剂的泄漏等对指示功率造成的影响，这些因素虽然对计算结果影响比较小，但终究还是会引起一定的误差；另外，推导的机理模型在各种工况条件下进行计算时其计算精度也最终会引起其计算值与实验值之间产生一定误差。

4 结论

基于工程实际，采用机理分析，根据工程热力学理论，构建制冷压缩机功耗随其主要热力学参数吸、排气压力变化的定量关系式。以某生产厂家生产的NS1112Y型压缩机为样机，在小型制冷压缩机性能测试台进行测试，分别比较了排气压力pd为0.7713 MPa、0.7113 MPa、0.6613 MPa、0.6113 MPa和0.5613 MPa下，pd分别为0.03743 MPa、0.04243 MPa、0.04743 MPa、0.05243 MPa、0.05743 MPa、0.06243 MPa、0.06743 MPa、0.07243 MPa、0.07743 MPa、0.08243 MPa、0.08743 MPa、0.09243 MPa时的压缩机功耗计算值和实验值，这60组数据比较显示，制冷压缩机功耗的计算值与实验值最小相对误差为0%，最大相对误差为4.64%，平均相对误差为2.75%，计算值与实验值基本吻合，能够满足工程设计精度要求。实验结果表明，本文构建的定量关系式模型基本能够准确描述制冷压缩机功耗与其主要热力参数吸、排气压力间的关系，说明文中推导的压缩机功耗计算式计算结果可靠，可用于工程实践。