空压站压力流量控制的理论分析及实验建模
2019-04-04杨洋,赵军,尚昆,吴丹
杨 洋,赵 军,尚 昆,吴 丹
(上海理工大学,上海200082)
1 引言
随着科学技术的进步和工业的发展,高压气体的应用越来越广泛[1,2]。但由于气体的可压缩性远大于液体的可压缩性,气体压力特别是高压气体的压力和流量更是难以精确控制[3]。压缩空气系统的效率偏低,浪费严重等问题也逐渐引起国内外学者们的重视[4-10]。
传统空压站通过提高整个系统的供气压力,使系统在大负荷事件发生时,其压力波动的最低点仍然高于对压力要求最苛刻的用气设备的压力需求。这就导致了空压站在整个运行时间内系统的供气压力始终高于系统实际的压力需求,系统的耗气量也随之增加,最终使整个空压机系统的能耗大幅度增加[11]。压力流量控制系统安装于供气端和用气端之间,主要作用是通过控制储气罐内的压力和阀门的开度从而控制系统的耗气量。压力流量控制系统可以稳定系统压力的波动,可以以恒定的供气压力和供气流量满足生产生活的需求[12]。而压力流量控制的数学模型,则是建立压力流量控制系统的前提。
2 实验系统
2.1 实验原理及实验装置
实验系统如图1所示,主要由空压机、冷干机、稳压罐、压力变送器、热式流量计、单座阀等部件组成。
在容积式空压站的运行过程当中,空气经压缩机压缩过后,通过直管段1流入冷干机进行冷却除湿,经过冷却除湿后的空气经过直管段2汇集到稳压罐中,稳压罐可以降低系统压力的波动,使系统的设备稳定运行。储存在稳压罐中的压缩空气最终通过直管段3输送到工业用气的各个环节之中。本实验直管段3管径为DN40,出口负载管径为DN20。
压力流量控制系统安装于供气端和用气端之间,即如图1所示的直管段3。本文主要通过控制单座阀在不同开度的工况下,通过数据采集系统测得稳压罐中的压力,直管段3的排气压力以及排气流量。利用Matlab拟合工具箱的数据处理功能,采用基于最小二乘法的多项式拟合的方法处理实验数据,建立排气压力,体积流量分别关于稳压罐中的压力和单座阀开度之间的数学关系。
数据采集系统通过USB2805C数据采集卡采集表1所示的测量仪表的输出信号,各被测参数首先由相应的测量仪表转换成电信号,然后该电信号经过信号调理电路,转换成标准模拟电信号,最后通过数据采集卡的模拟输入通道进行A/D转换后,生成可以被计算机识别的数字信号。数字信号的处理由计算机通过软件来完成。
2.2 节流元件
本实验采用ZJHP气动精小型单座阀来控制空压站输出的压力和流量,其由ZHA(B)型气动多弹簧薄膜执行机构和VJP型低流阻直通单座阀组成。单座阀的主要结构示意图如图2所示,其主要参数如表2所示。
3 压缩空气理论压力流量模型
3.1 排气压力模型
根据气体管道通用计算方法,可以知道稳压罐内的压力等于稳压罐和排气压力测点之间的总沿程压降损失、总局部压降损失和排气压力三者之和,设0为入口状态,2为出口状态,则可得到[13]

式中 p2——排气压力,Pa
p0——稳压罐内的压力,Pa
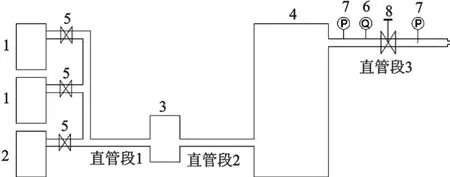
图1 实验系统示意图
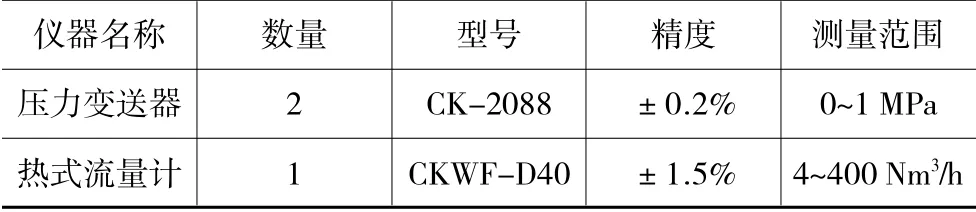
表1 测量仪表
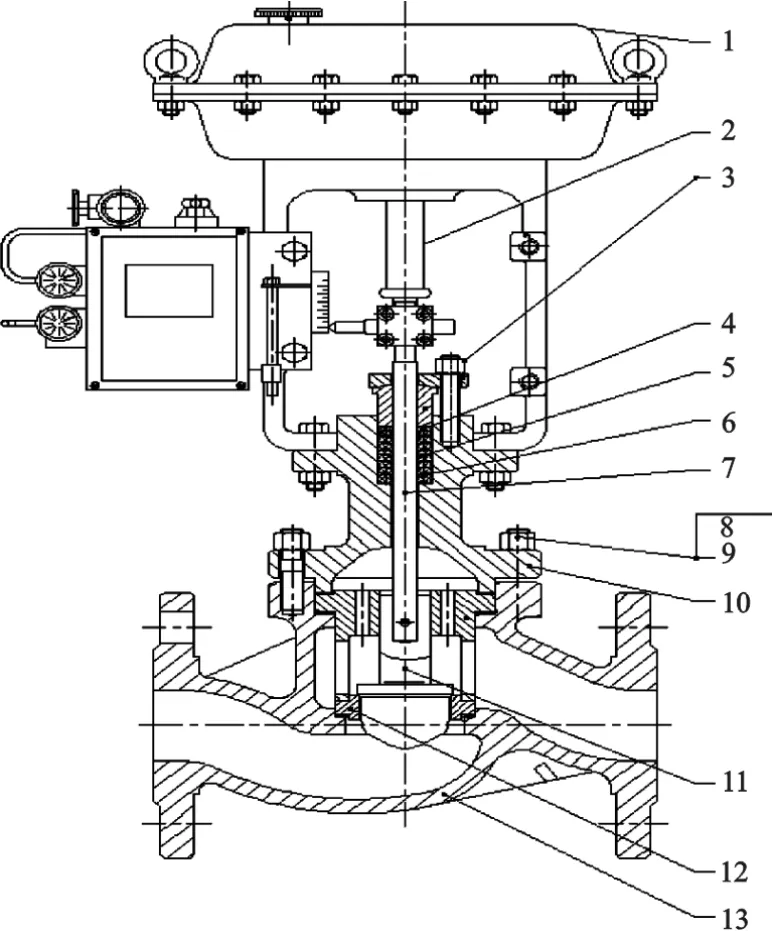
图2 单座阀结构示意图

表2 单座阀主要参数
pf——沿程压降损失,Pa
pζ——局部压降损失,Pa
由图1可知,直管段3中总沿程压降损失为一定值,总局部压降损失只和单座阀的开度有关。于是可以知道排气压力p2,与稳压罐内的压力p0和单座阀的实际行程h有关。
3.2 质量流量模型
根据热力学第一定律:热量可以从一个物体传递到另一个物体,也可以与机械能或其他能量互相转换,但是在转换过程中,能量的总值保持不变。即Q=ΔU+W。可推导出绝热流动下的能量方程为。

式中 v——速度
k——绝热指数
p——压力
ρ——密度
忽略空气的粘性,即流动过程为等熵流动,引入等熵关系式。

所以质量流量G=ρ2A2v2。考虑极限情况,当出口截面上的压强为临界压强时,流量达到最大值,出口速度为音速,此时对于空气来讲,k为1.4,所以此时p0=1.89p2。综上所述,我们可以得到压缩空气的质量流量模型如下所示[14]。当p2≤p0≤1.89p2时,可得
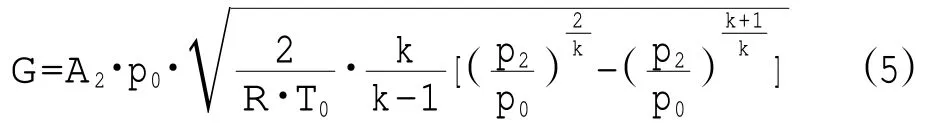
当1.89p2≤p0时,可得

式中 A2——出口的有效截面积,m2
p0——稳压罐内的压力,Pa
p2——排气压力,Pa
T0——稳压罐内空气的热力学温度,k R——气体常数,287.05J/(kg·k)
k——绝热指数
由压缩空气的质量流量模型(5)和(6)可知,质量流量只和p0、p2、A2以及T0有关。但在实际的容积式空压站中,空气的流动近似于绝热流动,经过冷干机流入到稳压罐中的空气,其温度基本变化不大,因此在实际运行过程中,可以把T0看成一个常量,即不需考虑T0的影响。因此可以将质量流量G看成是一个只和p0、p2、A2这3个量相关的一个量。
3.3 体积流量模型
在实际的工业应用当中,现场更多讨论的都是体积流量,于是在上文给出的质量流量模型的基础之上,接着给出体积流量模型。
体积流量公式:Q=A2v2,将公式(3)带入并且引入气体状态方程p=ρRT可得
当p2≤p0≤1.89p2时

式中 A2——出口的有效截面积,m2
p0——稳压罐内的压力,Pa
p2——排气压力,Pa
T0——稳压罐内空气的热力学温度,k
R——气体常数,287.05J/(kg·k)
k——绝热指数
分析式(7)和式(8),可知:体积流量Q只和p0、p2、A2这3个量有关。
3.4 小结
通过上文的分析可以知道排气压力p2只和稳压罐内的压力p0和单座阀的实际行程h相关。在实际实验当中,可以用阀门的开度来代替这个有效截面积,在本文中,用单座阀的实际行程h来代替有效截面积A2。于是可得体积流量Q和p0、p2、h相关,且p2又可以看成是一个只和p0和h相关的量,于是体积流量Q其实也就只和稳压罐内的压力p0和单座阀的实际行程h相关。因此可以通过控制单座阀的实际行程h,采集不同稳压罐压力p0下对应的排气压力p2和体积流量Q来进行实验,对实验数据进行汇总处理。
4 实验数据的处理
4.1 多项式的拟合
科学研究课题中,有时候我们需要建立几个变量之间的关系,但实际的数学之间的关系式并非线性的,我们就要根据n对实验数据(xi,yi,zi)找出这种函数关系z=f(x,y)。但这种函数关系往往很难通过理论分析得到,我们便可根据数据点的拟合假定其为一多项式,并求出多项式的阶数及系数,这称为多项式的拟合[15]。
本文主要依据多组实验数据,通过控制单座阀的开度,保持单座阀的开度不变,采集在不同开度之下稳压罐内的压力p0,排气压力p2,体积流量Q的n组实验数据,利用Matlab拟合工具箱,采用多项式拟合结合最小二乘法对实验数据进行处理,建立其数学模型。
从上文的分析可知,为了后续压力流量控制系统的建立,需要构建排气压力p2关于稳压罐的压力p0和单座阀实际行程h的数学表达式以及体积流量Q关于稳压罐p0和单座阀实际行程h的数学表达式。以排气压力p2关于稳压罐的压力p0和单座阀的实际行程h的关系为例,故可认为排气压力p2是关于稳压罐的压力p0和单座阀的实际行程h的二元函数,即p2=f(p0,h)。可用多项式拟合的方法构造出排气压力与稳压罐的压力和单座阀实际行程的关系式,其模型通式为
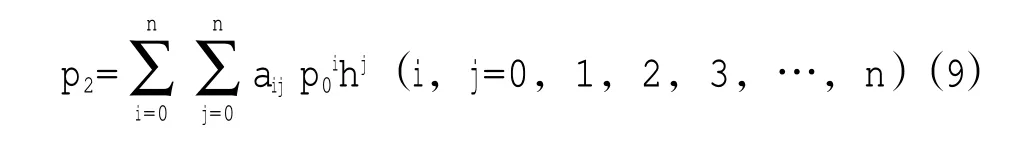
式中 p2——排气压力
n——多项式的最高次幂
aij——多项式的系数
p0——稳压罐的压力
h——单座阀的实际行程
拟合函数由多项式系数aij(i,j=0,1,2,…,n)确定,Matlab的拟合工具箱则是通过最小二乘法拟合出多项式的系数。
4.2 实验建模
根据实验数据,结合上述多项式的拟合方法,利用Matlab拟合工具箱的拟合程序可以求解得排气压力与稳压罐的压力和单座阀的实际行程的关系式如式(10)所示,并可得到排气压力模型的三维曲面如图3所示。

同样根据上式(9)的多项式拟合的方法,利用Matlab拟合工具箱的拟合程序可以求解得体积流量与稳压罐的压力和单座阀的实际行程的关系式如式(11)所示,并可得到体积流量模型的三维曲面如图4所示。
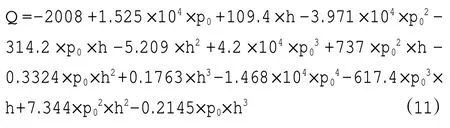
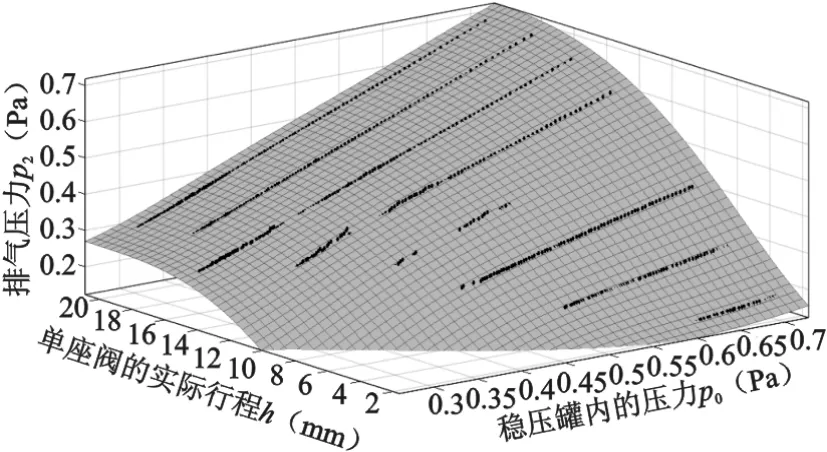
图3 排气压力模型的三维曲面
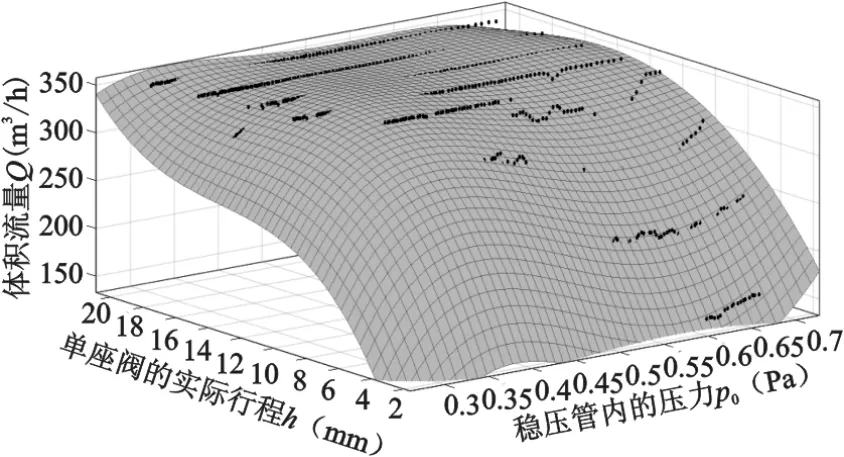
图4 体积流量模型的三维曲面
所以式(10)和式(11)就是排气压力和体积流量,根据实验数据拟合后分别关于稳压罐的压力和单座阀的实际行程的数学模型。
5 结论
通过对比压缩空气的理论压力流量模型和通过拟合实验数据建立的数学模型,可以得到以下结论:
(1)可以通过压缩空气的理论压力流量模型来指导我们的实验,通过对压缩空气理论压力流量模型的推导,我们可以知道排气压力和体积流量,只和稳压罐中的压力和控制阀门的开度有关。
(2)在实际的实验过程当中,考虑到空压站不可避免的漏气,控制阀门的多样性以及其内流场的复杂性等情况,这就导致了所推导的理论流量模型在实际的应用中存在很大的误差。而通过对实验数据的拟合得出来的数学模型则可以将现场的所有情况考虑进去,具有很强的应用性,可以为后续压力流量控制系统的建立提供数学模型,从而降低工业空压站的能耗。
(3)通过实验数据拟合的出来的数学模型具有一定的预测性,对实验未涉及到的工况具有一定的预测作用。
