基于自适应低秩去噪的近似消息传递压缩感知恢复

熊承义，陈仕长，高志荣，李世宇，金鑫，李治邦

(1 中南民族大学 电子信息工程学院，智能无线通信湖北省重点实验室，武汉430074；2中南民族大学 计算机科学学院，武汉 430074)

压缩感知(Compressive Sensing,CS)[1]是一种新的信号采样理论.它指出，利用信号的稀疏性，可实现突破传统奈奎斯特采样的信号压缩采样与准确重构.具体地，基于压缩感知理论，当信号满足稀疏性并且观测矩阵满足有限等距原则(Restricted Isometry Property，RIP)时，由降维观测值y∈RN可以高概率地准确重构原始信号x∈RN.

压缩感知重构是压缩感知理论成功应用的关键问题之一，其实现的数学模型可表示为

(1)

其中Φ为稀疏变换矩阵，A为测量矩阵，‖·‖是取p范数.

最初的CS重构算法运用凸规划方法，但是当处理图像这种高维信号时，这些凸规划方法十分耗时.因此，低时间复杂度的迭代算法得到发展，包括正交匹配追踪、迭代软/硬阈值以及近似消息传递算法[2].特别地，由Donoho和Maleki等人提出的低复杂度、高性能的迭代算法——近似消息传递算法(Approximate Message Passing，AMP)在运行速度及重构质量上具有更加明显的优势，因而更适用于高维信号的重构.

对于自然图像压缩感知重建，寻找合适的稀疏变换矩阵Φ，对提升压缩感知重构性能十分关键.基于AMP的图像重构算法常利用图像在小波域上的稀疏性作为重构的先验信息[3]，如基于小波振幅尺度不变贝叶斯估计、基于小波自适应Wiener滤波[4]和基于柯西分布最大后验估计的小波域AMP算法[5]，然而小波系数稀疏约束并不适用于包含较多非平滑部分的自然图像.为了解决这一问题，对边缘和纹理较好保留的梯度稀疏先验以及对图像单一子块进行稀疏表示的方法被开发出来，来改善AMP重构CS图像的质量.尽管这两种图像先验都具有一定的有效性，但他们仅利用了图像的局部特征，却忽略了图像中大量相似块含有的非局部信息[6,7].针对这种情况，Dabov等人开发了一种利用非局部相似块组在稀疏3-D变换域中协同滤波的图像去噪策略(BM3D)[6]，通过对非局部相似块组进行小波域稀疏变换及阈值处理，成为有效的图像恢复手段.文献[7]进一步挖掘图像的非局部结构特性，提出了一种基于非局部相似块组的低秩正则化模型，实现了对非局部相似块组自适应稀疏表示.文献[8]构建了基于去噪的AMP(Denoising-based AMP，D-AMP)方案，利用经典的图像去噪算法实现AMP迭代过程中的滤波操作，其中结合BM3D图像去噪算法的BM3D-AMP，获得了优于当前基于AMP方法的图像重构性能，然而该算法引入的BM3D算法对相似块组采用的是固定基小波稀疏变换，忽略不同块组的结构变化，无法获取每个相似块组的自适应稀疏表示，因而对非平稳图像的重构质量还需提高.

为了进一步改善图像压缩感知恢复性能，本文提出了一种自适应低秩去噪的近似消息传递压缩感知恢复方法.基于近似消息传递框架，对AMP迭代滤波图像进行噪声方差估计，根据噪声方差大小自适应调整图像分块的大小以及相似块组的规模来构建低秩矩阵，并对其采用加权奇异值软阈值处理实施低秩逼近，将相似块组在像素域的去噪逼近转化为对奇异值的软阈值滤波实现，不仅提高了对不同图像块组滤波的自适应性，也更好地刻画了图像的非局部自相似特征，保留了组内图像块之间的细微差异.实验仿真结果验证了该方法有效性.

1 相关工作

1.1 基于AMP的图像CS重构

近似消息传递是一种基于消息传递机制的迭代阈值信号恢复方法，具有快速收敛性和非线性求解能力.针对图像CS信号重构，该方法具有明显优势.对于式(1)压缩感知信号重构的数学模型，应用于图像CS重构时，根据AMP算法理论，可以用迭代公式求解表示如下

(2)

(3)

若令qt=xt+AT×zt，根据AMP算法特性，qt可以近似看成是被加性高斯白噪声污染的含噪原图像，可表示为qt=x+nt，其中nt∈RN符合零均值高斯分布.则基于AMP重构CS图像x的迭代公式可转化为如下式.

(4)

(5)

1.2 噪声水平估计

噪声水平是图像处理领域(如，图像去噪、图像分割和超分辨率等)中的重要参数.实际应用中，特定图像的噪声水平可能无法获取，因而需要进行估计.目前广泛用于图像恢复的重要噪声模型是加性高斯白噪声，对于给定的一幅噪声图像，噪声水平估计的目标就是近似获取其附加的高斯噪声的标准差σ.

对于观测到的噪声图像I∈M×N，借鉴文献[9]提出的方法可以精确的获取其估计值，具体步骤如下.

2 自适应低秩去噪的AMP图像CS恢复

2.1 改进的自适应图像低秩去噪算法

在图像获取与传输过程中，噪声的干扰是不可避免的，如何去除这些噪声是图像恢复领域的重要部分.图像去噪具体来说就是求解一个逆问题，利用有效的图像先验能够提升恢复图像的质量.针对以往固定基变换不能很好处理图像不同区域细节纹理的问题，近年来，利用图像的非局部低秩先验，对图像不同部分自适应稀疏表示的方法，取得了显著的去噪成效.

如何更有效地获取相似程度高的非局部相似块组是低秩去噪的关键.尽管目前的低秩去噪算法取得了很好的去噪性能，但是实际应用中，该算法在对一幅随机图像执行去噪时，由于图像受到的噪声污染程度是未知的，因而很难对其噪声方差进行准确估计，相应的低秩矩阵构建影响参数只能凭借经验设定，然而凭借经验得到的噪声方差并不精确，导致实际去噪后的效果不理想.并且在噪声水平不确定的情况下，为了得到更好的去噪效果，只能通过多次实验进行比较得到，所付出的时间成本相对较大.

为了更加快速有效地获取低秩矩阵构建的影响参数，进而实现自适应低秩去噪.考虑到不同噪声水平下图像块大小以及相似图像块个数对低秩去噪性能的影响，从图像数据集库中选取多幅自然图像进行实验统计，获取不同噪声环境下更优的低秩矩阵构建方法.具体实验时，对干净图像进行加噪处理后实施不同分块以及不同相似块个数进行低秩去噪实验，观测最终达到最佳峰值信噪比(Peak Signal-to-NoiseRatio，PSNR)时的这两类参数设定.实验中，发现一定范围内的噪声标准差变化对图像PSNR的影响微弱，因此给出分段噪声情况下最佳参数设定如表1所示.

表1 分段噪声标准差下图像低秩去噪最佳块大小以及相似块个数Tab.1 Low-rank image denoising optimal block size and number of similar blocks under standard deviation of section noises

根据以上分析，提出一种改进的低秩去噪算法.利用1.2节噪声估计方法，对含噪图像进行噪声估计，并按照噪声水平分配块大小以及相似块个数，快速自适应地获取最优低秩矩阵构建的影响参数，然后，通过块匹配搜寻噪声图像的非局部相似块，构建具有低秩特性的非局部相似块组，并通过求解该低秩矩阵自适应稀疏表示进行低秩逼近，实现去噪.

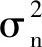
(6)

(7)

(8)

c2=σi(Yj)-ε,c2=(σi(Yj)+ε)2-4C.

通过将上述步骤应用到每个分块并将所有处理后的分块组合，然后对重叠的图像块求平均，图像X就能被复原，并多次迭代获取更佳的去噪图像.

2.2 提出的CS图像重构方法

输入 测量矩阵A∈RM×N，测量向量y=Ax+ω∈RM，迭代次数m.

初始化 令x0=0,z0=y.

迭代运行

(1)CS反投影计算含噪图像qt-1=xt-1+AT×zt-1；

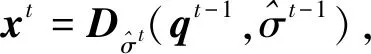
(4)随机生成N维变量b=randn(1,N)∈N(0,1)，

(5)求去噪函数的散度

(7)残差更新zt=y-Axt+Onsagert；

结束迭代

3 实验结果与分析

为了验证本文方法的重构性能，分别在有、无测量噪声(对测量值进行加噪)情况下将本方法与BM3D-AMP、TV-AMP、NLM-AMP、LR-AMP四种方法进行CS重构仿真比较.选取常用的自然图像(大小为128×128像素的灰度图像)作为测试图像，以PSNR作为算法重构性能的衡量.

实验中，将本文方法迭代次数设定为20次.根据AMP每次迭代滤波逆投影输入图像的噪声标准差估计，对含噪图像进行自适应低秩去噪处理.对于LR-AMP算法，其在AMP滤波去噪阶段，采用固定的块大小和相似块数目，本文方法采用表1中最优参数进行低秩矩阵构建.其余参数设置与自适应低秩去噪算法相同，块间距step=5，搜索窗的尺寸为30×30，松弛参数δ=0.1，缩放因子γ=0.58.仿真计算机的硬件配置为Intel(R)Core(TM)i7-6700 CPU，3.40 GHz 主频，软件环境为64位Windows7操作系统下的Matlab 2015a.

首先，五种方法在无测量噪声情况下，分别在测量率为0.1/0.2/0.3时进行仿真实验.五种重构方法的图像恢复质量PSNR比较结果如表2所示.实验结果比对可见，不同采样率下，本文方法的值基本上最高，证明本文方法具有更好的客观重构性能，也说明改进的自适应低秩去噪算法能够有效提升本文方法的重构性能.由表中平均值可以发现，本文方法比TV-AMP、NLM-AMP、BM3D-AMP、LR-AMP方法PSNR分别提高了6.67、5.44、1.32和0.28dB，验证了本文方法的有效性.

表2 不同采样率下各种方法PSNR结果比较Tab.2 Comparison of PSNR results of various algorithms at different sampling rates

图1对Leaves重构图像局部进行放大处理，可以观察到，相比TV-AMP重构，结合图像非局部相似性的重构方法均取得了较好的重构效果.由TV-AMP重构局部放大(图1(b))可以明显看到过平滑现象，在几种采用非局部相似性的重构方法中，NLM-AMP利用非局部相似块的均值来估计当前像素块，这种估计放大会带来振铃效应，因此重构图像边缘纹理较为模糊.而BM3D-AMP利用图像的非局部相似性先验，虽然重构效果较好，但仍不能精确重构原图像，而LR-AMP和本文方法采用非局部低秩先验来自适应估计相似块组，对细节处理较好，并且本文方法采用自适应策略，能够进一步保留有效信息，因而具有更好的主观视觉效果.

图1 测量率为0.3 时Leaves图像的重构质量比较Fig.1 Comparison of reconstruction quality of leaves image at a measurement rate of 0.3

进而，为了验证本文方法在有测量噪声情况下的鲁棒性，由于篇幅限制，仅给出五种方法在采样率为0.2时含噪情况下的重构性能比较如表3所示.与无噪观测相比，存在噪声干扰测量值时，各种方法的PSNR都有所降低，但本文方法的值继续保持最高，验证了本文方法的抗噪声干扰性能.同时由表中平均值数据可知，在测量率为0.2时，本文方法比TV-AMP、NLM-AMP、BM3D-AMP、LR-AMP算法PSNR分别提高了3.04、2.52、0.54和0.15dB，验证了本文方法的鲁棒性.

表3 测量率0.2时，不同噪声标准差情况下图像重构PSNR比较Tab.3 Comparison of image reconstruction PSNR under different noise standard deviations when the measurement rate is 0.2

图2 测量率为0.2、噪声标准差为20时Leaves图像的重构图像比较Fig.2 Comparison of reconstructed images of lefts images with a measurement rate of 0.2 and noise standard deviation of 20

图2从主观视觉角度比较本文方法与其他四种方法在外加测量噪声情况下重建图像的效果.在外加测量噪声标准差20、测量率0.2情况下重构Leaves图像，TV-AMP、NLM-AMP重构图像较差，LR-AMP重构图像视觉效果优于BM3D-AMP,本文方法实现较好的重构效果，同时从局部放大可以看出，本文方法较LR-AMP有较好的细节重构性能.

图3(a)和(b)分别给出了在采样率为0.3、无观测噪声时对House图像重构以及在采样率为0.2、观测噪声标准差为20时对Barbara图像重构得到的PSNR～迭代次数曲线图.几种基于AMP的方法都有较好的收敛性，本文方法在基于AMP框架的基础上结合图像低秩特性以及自适应策略实现了收敛性和重构质量PSNR双重性能保障.

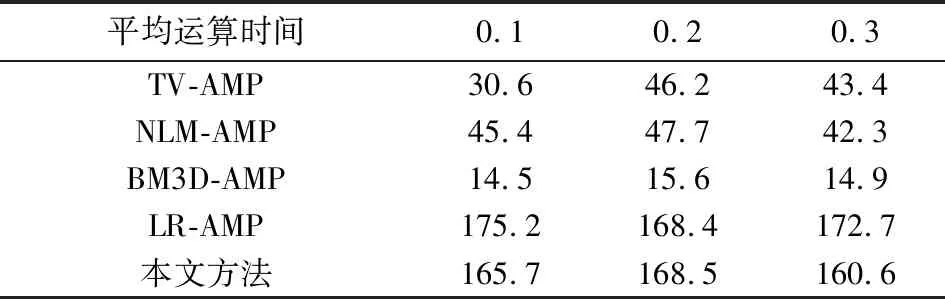
最后，给出五种方法运行时间的比较，实验结果如表4所示.由表中可以看出，BM3D-AMP在不同采样率下运行时间最少，这是因为该方法运用的BM3D滤波算法采用c语言编译，速度快.本文方法在低秩矩阵的奇异值分解上耗时较大，因而在运行时间上优势不足，但对于实际应用中着重重构质量的情况，该方法有明显优势.

图3 5种算法对两幅图像重构得到的PSNR～迭代次数曲线图Fig.3 PSNR ～ iterations curves of five algorithms for Barbara image reconstruction

平均运算时间0.10.20.3TV-AMP30.646.243.4NLM-AMP45.447.742.3BM3D-AMP14.515.614.9LR-AMP175.2168.4172.7本文方法165.7168.5160.6

4 结语

针对自然图像压缩感知恢复问题，提出一种自适应低秩去噪的近似消息传递CS图像重构方法.将利用图像非局部相似性先验的低秩去噪算法作为AMP迭代滤波的去噪函数，实现图像CS重构；并研究不同噪声大小图像进行自适应低秩矩阵构造来实现更优图像重建，自适应滤出AMP迭代噪声，最终提升CS图像重构质量.实验结果表明，该方法的图像重构性能优于BM3D-AMP等，对图像非平稳部分恢复较好.