基于模拟退火法优化的MMC二次环流计算方法

谭风雷，陈昊，张兆君，朱超，张建忠

(1 国网江苏省电力有限公司检修分公司，南京 211102；2 东南大学 电气工程学院，南京 210096)

随着特高压电网在国内的快速发展，国家电网已累计建成“三交四直”特高压工程，在建“四交五直”特高压工程，标志着特高压电网时代的来临.近几年来，直流特高压凭借其输送功率大、距离远、损耗小的优势得到了广泛的关注[1].目前，特高压直流输电工程中换流阀主要采用半控型器件晶闸管SCR，但存在容易发生换相失败，需要大量的无功补偿装置和滤波设备，甩负荷时容易过电压等缺点，从而使得基于全控型半导体器件IGBT(绝缘 栅双极晶体管)的柔性直流输电技术[2]应运而生，舟山多端柔直工程[3]是我国第一个柔直示范工程，但全控型半导体器件IGBT功率较小，从而也限制了柔性直流技术的发展.随着材料科学的不断发展，全控型半导体器件IGBT功率越来越大，柔性直流输电技术代替传统的直流输电技术是不可抗拒的趋势.模块化多电平技术作为柔性直流输电技术的一部分，必将是现在乃至未来一段时间的研究重点.

目前，针对模块化多电平技术研究的文献已经相对较多，主要集中在研究模块化多电平换流器的数学模型、运行机理、调制技术、电容电压控制策略、模块冗余配置方法、系统故障分析及其处理措施等.文献[4]将模块化多电平换流器当作电压受控源，建立了等效电路及其数学模型.文献[5]提出了基于载波移相的分层控制方法，包括能量均衡控制和电容均压控制两个部分，最后借助实验验证了控制策略的有效性.文献[6]在深入分析模块冗余的基础上，提出了冗余度与可靠性的概念，并从MMC系统可靠性、冗余子模块有效利用率和冗余子模块数量三个方面出发，提出了一种基于多目标优化的MMC模块冗余优化配置方法.文献[7]研究了MMC-HVDC子模块故障诊断技术和就地保护策略.尽管模块化多电平技术已经比较成熟，但是依然存在一些难题有待发现和解决.

桥臂电流主要包含直流分量、基频分量以及二倍频分量，其中直流分量和基频分量与输出功率有关，因此只能通过抑制二倍频分量来减少桥臂电流，降低功率器件的损耗.文献[8]推导得到了二次环流表达式，但推导过程忽略较多使得结果不够准确且未对二次环流做详细分析.文献[9]在分析了二次环流形成原因的基础上，提出了水平环流抑制、垂直环流抑制以及加装滤波器控制三种二次环流的抑制方法，但效果和实用性不佳.基于上述的分析，本文将从电容伏安特性和等效开关函数角度出发，将桥臂能量均衡控制环节简化为双比例调节器后，推导得到了二次环流幅值计算模型，该模型可以为减小二次环流幅值提供理论依据.同时为了进一步提高二次环流的计算精度，建立了二次环流修正模型，并采用了基于最小二乘法优化的模拟退火法求解最优参数.最后，通过仿真结果验证了计算模型和修正模型的可行性和有效性.

1 MMC拓扑结构及其控制方法

1.1 MMC拓扑结构

MMC拓扑结构如图1所示，由六个完全相同的桥臂组成，每个桥臂由N个功率子模块(SM)和一个桥臂电抗器Ls级联而成，上、下两个桥臂构成一相，图中Udc为直流母线电压，ia、ib、ic分别表示MMC三相的输出电流，而ua、ub、uc分别表示MMC三相的输出电压.MMC的基本工作原理：

(1)为了维持直流母线电压不变，减少桥臂环流，须保持上、下桥臂投入的子模块数量之和为N.

(2)通过调节上、下桥臂投入子模块的数量，从而改变输出电压的大小.

图1 MMC拓扑结构图Fig.1 Circuit configuration of MMC

1.2 MMC控制方法

目前，MMC控制方法主要分为两种：基于电容电压排序的直接调制方法和基于载波移相的分层控制方法[10].本文将重点研究基于载波移相的分层控制方法，该方法的调制波[11]主要分为四个部分：直流电压信号，参考电压信号，桥臂能量均衡控制信号和电容电压均压控制信号.MMC调制电压信号控制原理如图2所示.表达式可以表示成：

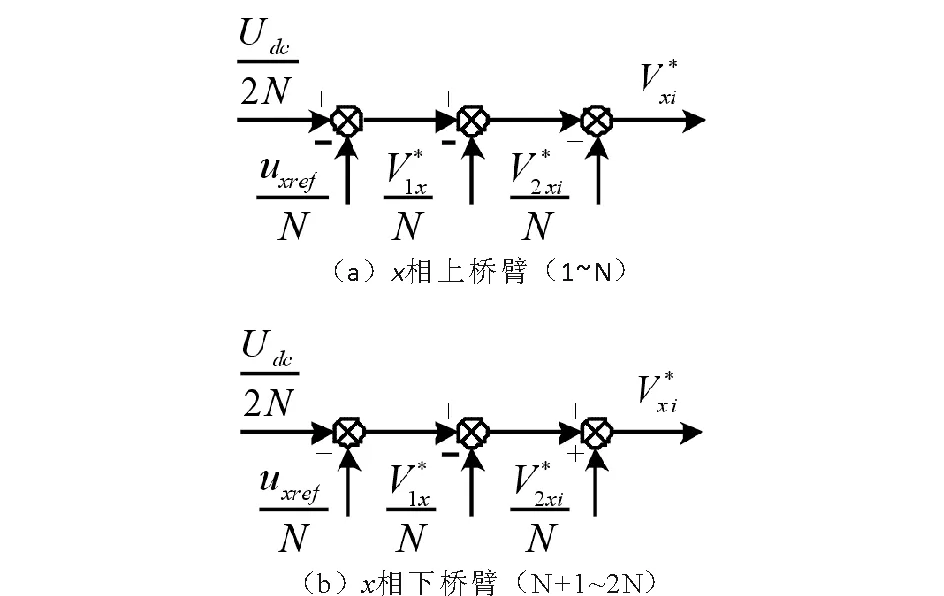
图2 MMC调制电压信号控制原理图Fig.2 Modulated voltage signal of MMC

(1)

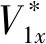
2 二次环流定量计算

根据电容伏安特性，结合等效开关函数，可以来分析电容电压波动规律[10,11].假定MMC输出电压ux和输出电流ix可以表示成：

(2)

式中，Us为输出电压的幅值，Is为输出电流的幅值，ws为输出电压的频率，θx为输出电压的相角，φ为电流滞后电压的相角，x取值为a、b、c.

为了简化分析，忽略掉表达式(1)中桥臂能量均衡控制环节和电容电压均压控制环节的信号输出，归一化后可以得到上、下桥臂等效开关函数：

(3)

式中，Spx和Snx分别为x相上桥臂和下桥臂的等效开关函数表达式.

桥臂电流中主要含有直流分量，基波分量和二次分量[12].为了简化分析，忽略掉环流中的二次谐波分量，并假设三相桥臂均匀承担直流母线侧电流，则上桥臂和下桥臂电流可以表示成：

(4)

式中，ipx和inx分别为x相上桥臂和下桥臂电流，Id为直流母线电容侧直流电流，该电流与交流输出侧功率有关.

根据MMC子模块电容的伏安特性，并结合式(3)和(4)，则x相上桥臂和下桥臂单个子模块电容电压的波动情况可以表示成：

(5)

为了简化计算过程，下面的分析都以a相为例.根据a相上桥臂和下桥臂单个子模块电容的电压表达式，可以得到a相上、下桥臂总电压Upna，具体的推导过程可以参见文献[13].

Upna=Upa+Una=

(6)

根据上、下桥臂电压之和等于直流母线电压，可以得到二次环流的幅值和相角.

(7)

式中，IZ为二次环流的幅值，φZa为a相二次环流的相角.

3 二次环流定量修正

桥臂能量均衡控制环节是通过调整相间环流来重新分配能量，达到三相桥臂间均衡控制，属于桥臂间能量调整，对环流影响较大，而电容电压均压控制环节则是通过调整桥臂内能量，达到子模块电容电压的均衡，属于桥臂内部能量调整，对环流影响相对较小[13,14].为了便于分析，式(3)中计算等效开关函数时，忽略了桥臂能量均衡控制与电容电压均压控制环节，这样导致等效开关函数和实际值存在差异，从而使得二次环流幅值与相角计算偏差相对较大.为了进一步提高运算精度，同时简化分析过程，文中在计算等效开关函数时，忽略电容电压均压控制环节，而仅考虑桥臂能量均衡控制环节.

桥臂能量均衡控制环节是通过补偿桥臂电感压降来修正调制电压信号，使得调制波更加准确，从而实现三相能量均衡控制.桥臂能量均衡控制环节由电压外环和电流内环两部分组成，如图3所示.

图3 桥臂能量均衡控制环节原理图Fig.3 Averaging control

根据前面的分析，为了进一步简化推导过程，文中做出了三个假设：

1)只考虑环流中的直流分量与二次分量；

2)在稳态情况下，积分I调节器输出值较小且可忽略；

3)在稳态情况下，近似认为桥臂能量均衡控制环节的电压外环的输出直流分量与环流中的直流分量相等.

根据前面的假设，可以将桥臂能量均衡控制环节的双比例、积分PI调节器简化成双比例P调节器.将电压外环的积分环节忽略后，可表示成：

(8)

式中，KV1为电压外环比例调节器的系数，UC*为子模块电容电压的目标值，UCAVx为x相子模块电容电压的平均值，iZlx*为桥臂环流的目标值.

将电流内环积分环节忽略后，可表示成：

(9)

式中，izx为x相桥臂环流值.

a相子模块电容电压的平均值可表示成：

(10)

式中，UCpa和UCna分别为a相上桥臂和下桥臂单个子模块电容电压.

简化表达式(10)可得：

(11)

根据桥臂能量均衡控制环节的控制原理，将式(11)代入式(8)可得电压外环的表达式：

(12)

根据上面的假设，忽略电流内环输出的直流分量后，并将式(12)代入式(9)可得电流内环的表达式：

(13)

将式(13)代入式(3)，则修正后的等效开关函数可以表示成：

(14)

实际上，考虑到MMC子模块电容电压的波动与电容电压均压控制环节有关，且不受到桥臂能量均衡控制环节的影响，故在分析子模块电容电压波动时，假设等效开关函数修正前后对其影响较小，不予分析.因此，文中将重点研究等效开关函数修正后对上、下两个桥臂总电压的影响，将修正后的等效开关函数代入式(6)并忽略V1a*与小量的乘积后，可得a相上、下两个桥臂总电压Upna：

(15)

显然，a相上、下两个桥臂总电压的二次分量Upn2a与二次环流作用在两个桥臂电感上的压降相等，即：

4wsLsIzsin(2wst+φza)=

2KI1Izcos(2wst+φza).

(16)

求解表达式(16)可得二次环流的幅值与相角，如式(17)所示.

(17)

根据式(17)可知，二次环流幅值和相角不仅与功率(Us，Is，Udc，Id，cosφ)、模块数量N、电感Ls以及电压频率ws有关，而且在一定程度上还与桥臂能量均衡控制环节的两个P调节器系数(KV1，KI1)有关.

前面推导二次环流幅值和相角表达式时，为了简化计算过程，做出了一定假设，使得计算值与真实值略有偏差，为了提高计算精度，借助最小二乘法的思想，本文将重点对二次环流的幅值进行修正.考虑到二次环流幅值主要与输出功率以及两个比例调节器系数有关，结合式(17)建立了二次环流幅值偏差量修正模型：

(18)

则对应的二次环流幅值修正模型可表示成：

(19)

式中，IZ1为二次环流修正值，IZ0为二次环流初始值.利用二次环流实际值IZ*、输出电流Is以及两个比例调节器系数，采用基于最小二乘法优化的模拟退火法(LS-SA)[13]求解最优参数k1、k2、k3、k4和k5：

(20)

求解得到最优参数k1、k2、k3、k4和k5后，代入式(19)，即可得到二次环流幅值的修正表达式.

4 仿真分析与研究

为了验证本文所推导的二次环流幅值和相角表达式的正确性，在PSCAD软件中搭建了三相MMC换流器仿真模型，主要参数如表1所示.

二次环流幅值Iz随输出电流幅值Is变化曲线如图4所示.分析图4可知：二次环流幅值Iz与输出电流幅值Is、功率因数角φ、桥臂电感Ls、子模块电容C以及输出电压频率ws有关，随输出电流幅值Is和功率因数角φ的增大而增大，而随桥臂电感Ls、子模块电容C以及输出电压频率ws的增大而减小，与实际情况相符，同表达式(7)和(17)结论一致.

表1 模型参数

对比分析图4(e)和图4(f)可以发现：二次环流幅值Iz还与桥臂能量均衡控制环节比例调节器系数KV1、KI1有关，且随KV1的增加而增加，随KI1的增加而减少，从而验证了表达式(17)的正确性和有效性.

二次环流幅值Iz随主要参数变化曲线如图5所示.图5中，表达式(7)关于二次环流的计算结果简称为初始值，表达式(17)关于二次环流的计算结果简称为计算值，二次环流的仿真值简称为仿真值.分析图5可知：当KV1KI1=16且保持不变时，随着KV1和KI1的连续变化，初始值保持恒定，而计算值会随之变化而变化且变化趋势与仿真值完全一致；当CLs=4.7×10-5F·H且保持不变时，随着C和Ls的连续变化，初始值始终保持恒定，而计算值会随之变化而变化，且同仿真值的变化趋势完全一致；同理可以分析另外两种情况，从而再次验证了表达式(17)的正确性和有效性.

由于在推导二次环流幅值的过程中进行了多次假设，使得二次环流计算值与仿真值存在一定的差异，可参见图5.为了提高计算值的精度，文中采用最小二乘法的思想对计算值误差进行修正.具体的过程为：

步骤1：利用仿真得到的(KV1=0.8，KI1=10)，(KV1=0.8，KI1=20)，(KV1=0.4，KI1=20)三组数据(包括二次环流幅值和输出电流幅值)代入表达式(20)；

步骤2：采用基于最小二乘法优化的模拟退火法计算得到最优参数k1=1.8，k2=0.3，k3=-0.6，k4=100，k5=1.3；

步骤3：将最优参数(k1、k2、k3、k4和k5)代入表达式(19)，可以计算得到了二次环流的修正值.

图4 二次环流幅值 Iz随输出电流幅值 Is变化曲线( φ、Ls、C、ws、KV1、 KI1)Fig.4 Curve of Iz vs. Is for different φ、Ls、C、ws、KV1、 KI1 values

图5 二次环流幅值 Iz随主要参数变化曲线( Is=500A)Fig.5 Curve of Iz vs. main parameters( Is=500A)

图6 二次环流幅值 Iz随输出电流幅值 Is变化曲线(计算值、修正值和仿真值)Fig.6 Curve of Iz vs. Is(calculated value, correction value, simulative value)

二次环流幅值随输出电流变化曲线如图6所示，图中修正值是指通过表达式(19)计算得到的二次环流值，图6(a)表示当KV1为0.8且KI1为15时，二次环流幅值随输出电流变化曲线，图6(b)表示当KV1为0.6且KI1为20时，二次环流幅值随输出电流变化曲线，图6(c)表示当KV1为0.6且KI1为15时，二次环流幅值随输出电流变化曲线，显然不管KV1和KI1取值如何，都满足二次环流幅值计算值小于修正值，而修正值近似等于仿真值的结论，表明了本文所提出的修正方法的有效性.为了更加直观的对比修正效果，绘制了表2、3和4.显然，二次环流计算值小于仿真值，这是因为推导过程做出了相应假设；二次环流修正值与仿真值相差较小，用修正值代替仿真值作为二次环流的理论值是可行的，从而验证了表达式(19)的正确性.

表2 二次环流的计算值、修正值和仿真值(KV1=0.8，KI1=15)

Tab.2 Calculated value, correction value, simulative value for secondary circulation current(KV1=0.8，KI1=15)

电流幅值100200300400500仿真值4.7210.1315.5620.7726.07计算值4.699.3814.0818.7723.46修正值5.0210.2015.4620.7826.15

表3 二次环流的计算值、修正值和仿真值(KV1=0.6，KI1=20)

Tab.3 Calculated value, correction value, simulative value for secondary circulation current(KV1=0.6，KI1=20)

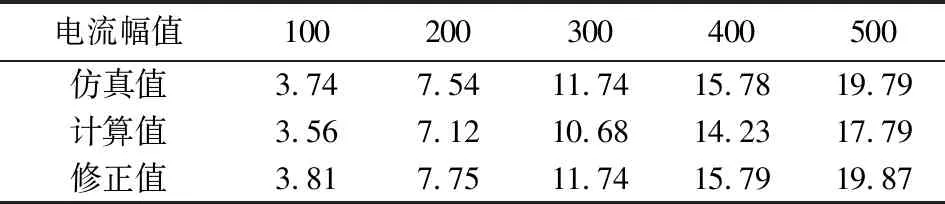
电流幅值100200300400500仿真值3.747.5411.7415.7819.79计算值3.567.1210.6814.2317.79修正值3.817.7511.7415.7919.87

表4 二次环流的计算值、修正值和仿真值(KV1=0.6，KI1=15)

Tab.4 Calculated value, correction value, simulative value for secondary circulation current(KV1=0.6，KI1=15)

电流幅值100200300400500仿真值4.108.3412.9917.4721.94计算值3.907.8011.6915.5919.49修正值4.208.5412.9617.4321.95

本文研究得到了二次环流幅值IZ与桥臂能量均衡控制环节KV1、KI1有关的重要结论.在保证系统稳定运行的条件下，合理选择KV1、KI1参数，可以有效减小二次环流幅值.该部分研究内容将在后续的文章中给予详细阐述.

5 结语

(1)根据电容伏安特性和等效开关函数，将桥臂能量均衡控制环节简化为双比例调节器后，建立了二次环流幅值计算模型.

(2)二次环流幅值随输出电流幅值Is和功率因数角φ的增大而增大，而随桥臂电感Ls、子模块电容C以及输出电压频率ws的增大而减小.

(3) 二次环流幅值与桥臂能量均衡控制环节KV1、KI1有关，且随KV1的增加而增加，随KI1的增加而减少.为在保证系统稳定运行的条件下，减小二次环流幅值，合理选择KV1、KI1参数提供了依据.

(4)采用基于最小二乘法优化的模拟退火法修正计算误差，得到了二次环流修正模型，通过仿真结果验证了该模型的有效性和可行性.