基于MCM全反射模型的镀锌层质量测量方法

徐巍，孔建益，刘宗赣，刘怀广，开岗生，王兴东

(1 武汉科技大学 冶金装备及其控制省部共建教育部重点实验室，武汉 430081；2 湖北邮电规划设计有限公司，武汉 430024;3 武汉钢铁股份有限公司 设备管理部，武汉 430083)

锌层的厚度与均匀性是镀锌钢板和钢带的重要质量标准，也在一定程度上影响着生产成本.近年，锌层厚度控制研究主要围绕工艺控制和建模预测两方面.工艺控制研究包含气刀设备改进[1]、气刀控制参数优化[2]、锌液成分[3]、浸锌时间[4]、带钢拉取速度[5]等方面；建模预测则是研究利用生产线参数构建数学模型对锌层厚度进行预测与控制[6，7].但从自动锌层厚度控制技术的角度，锌层厚度测量是工艺控制的前提与关键.只有通过锌层测厚仪获得实时数据，并与气刀配合参与反馈控制，才能实现自动厚度控制.国内大型钢铁联合企业的在线锌层测厚仪的测量方法为X射线荧光测量法[8].其将X射线源、电离室、高压装置和冷却装置均封装在一个测量头内[9].但由于X射线的穿透能力非常强，当采用常规X射线荧光测量法时，X射线穿透基体的量比锌层量大的多[10].从而导致镀锌板发出的荧光和比荧光能量大得多的散射光同时进入测量头[11，12]，提高了测量系统的本底并降低了测量精度和准确性[13].因此必须发展新型X射线荧光分析技术以适应对镀锌板检测的要求.

全反射X射线荧光技术是传统X射线荧光技术的延伸，通过全反射完全反射掉了原级X射线，使测量时辨别特征X射线荧光变得容易，提高了信噪比和降低了检测限，能够到达更高的测量精度.自Yoneda Y和Horiuchi T首先撰文介绍了TXRF(Total-Reflection X-ray Fluorescence)至今[14]，作为无损、原位分析技术，其优越性得到了充分的肯定[15].然而，TXRF技术在工业自动化与智能制造方面的研究较少.本文将TXRF技术与工业自动化研究相结合，讨论了将全反射X射线荧光技术应用到镀锌板锌层测量的可行性，提出一种基于TXRF技术的镀锌板锌层厚度测量方法.

1 实验

蒙特卡罗(Monte Carlo)方法，又称随机抽样技术，属于计算数学的一个分支，起源于20世纪40年代.它的基本思想是，为了求解数学、物理、工程技术以及生产管理等方面的问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，最后给出所求解的近似值.粒子输运问题具有随机性质，粒子的输运过程是一个随机过程.粒子的运动规律就是根据大量粒子的运动状况总结出来的，是一种统计规律.传统的经验方法不能逼近真实的物理过程，而蒙特卡罗方法能够真实地模拟实际物理过程.蒙特卡罗模拟，实际上就是模拟相当数量的粒子在介质中运动的状况，使粒子运动的统计规律得以显现.

MCNP(Monte Carlo Neutron and Photon Transport Code)[16]是美国Los Alamos国家实验室研制开发的一个利用蒙卡罗特方法解决粒子输运问题的大型多功能蒙特卡罗程序.通过MCNP程序能够建立TXRF技术应用于镀锌板测量的物理模型，为标准测量曲线的建立提供支持.

1.1 标准板制备

将某冷轧厂提供的镀锌钢板经试验钢板分条、试样筛选、锌层均匀性筛选、标准板赋值四步骤制备成镀锌标准板.具体方法为：

(1)沿钢板轧制方向，将钢板分切成条形试样.钢板边部的两条试样废弃，分切时应不损伤表面；

(2)观察表面，将表面有缺陷、色泽不均匀、不平直的样条废弃；选取一条作锌层均匀性筛选；

(3)将样条置于离线锌层测厚仪测量位置，沿样条中轴线扫描一次，再以中轴线为对称轴在两侧各扫描一次.若3条扫描线均匀一致，没有异常凸起(或下陷)的峰/谷，则在每条扫描线的两端和中部各作5次定点测量，得到15个测量值.求出平均值与标准偏差，若标准偏差/平均值≤2%，且任意测量值与平均值的差均小于三倍标准偏差，则样条上的该区域为入选区域.

(4)根据国家标准GB/T 1839《钢产品镀锌层质量试验方法》的测定结果对标准板给定标准值.

1.2 模型设定

设置模拟空间中充满空气，由C、N、O、Ar元素组成；标准镀锌板为圆形，其圆心位于MCNP仿真程序的原点坐标(0,0,0)处，直径为62.5 cm，厚度为0.15 cm，基材由Si、Cr、Mn、Fe、Ni、Mo元素组成；锌层由Zn元素组成，厚度为0.004cm；在镀锌板的正上方设置X射线荧光探测器以接收特征X射线荧光，与镀锌板的距离d=1cm.荧光探测器的壳体为圆柱体，底部设铍窗，其内充满惰性气体氩气.程序计数类型取为F2[17](穿过一个界面的平均通量，粒子数·cm-2)，可对通过荧光探测器界面的光子进行有效统计.为了使模拟趋近于实际情况，在模型建立的过程中引入核素(由元素的原子序数和质量数结合得到)和质量分数(元素所占的比例，程序中需带负号)的概念来表示材料的实际组成元素及其所占的比例[18].图1(a)所示分别为镀锌板基材核素与质量分数，图1(b)为模型各栅元分布示意图.

图1 MCM模型Fig.1 MCM model

1.3 射线源设定

当待测元素确定以后就需要根据其元素特性来确定临界激发能，图2所示为镀锌板主要的组成元素及其临界激发能.镀锌板锌层测量主要激发的目标元素是Zn元素.

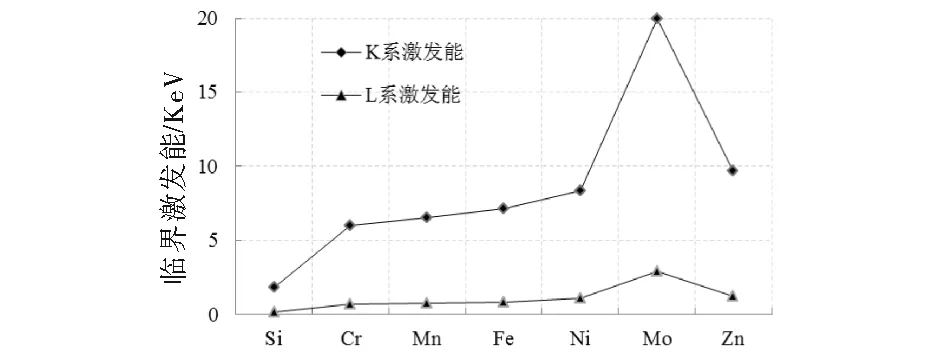
图2 元素临界激发能Fig.2 Critical excitation energy of different materials

由图2可知：当入射X射线光子能量大于或等于9.657 KeV的时候可以有效激发镀锌板的主要组成元素K系特征X射线荧光(一般K系的激发能远大于L系，且K系特征X射线荧光强度较高容易被检测).而X射线管发出的原级X射线谱是由连续谱与特征谱射线的迭加而成，这两种谱线在样本元素的激发过程中都扮演着至关重要的角色.根据特征谱与连续谱的计算关系可知，只有在管电压为激发电势的3～5倍时，特征X射线谱的强度最佳，可以提高对镀锌板锌层的特征X射线荧光的激发效率[19].所以在入射原级X射线光子的能量不变的情况下，为了提升原级X射线的强度，且不产生负面影响，取管电压为50 kV.

已知管电压大小，联立杜安-亨特公式和普朗克公式，可得最大光子能量的计算公式为

Emax=hvmax=hc/λ0=Uphc/12.42×10-10=

80.072463×10-16(J),

(1)

式(1)中，h为普朗克常数(6.63×10-34J·s)；c为光速(3×108m·s-1)；vmax为短波限对应的X射线频率；λ0为短波限；Up为X射线管的管电压；λ0和Up的单位分别采用m和kV.根据MCNP程序的输入格式，须将Emax的单位转换为电子伏特，则有Emax=5.0045×104eV.

最后由经典反射理论，在不考虑吸收限处的共振现象和量子效应的条件下，可推导出锌层表面理论全反射角的计算公式为

(2)

式(2)中，λ0为反射X射线的波长(2.484×10-9cm)；z为原子序数(30)；ρ为反射物质的密度(7.14 g·cm-3)；A为反射物质的原子量(65).根据MCNP程序的输入格式，须将αc的单位转换为度，则有αc=0.06004°.

通过理论全反射角度αc和Emax来建立物理模型中的X射线全反射光路，使X射线源发出的光子以入射角αi(αi<αc)照射到镀锌板上，在Y轴对称位置设置接收反射X射线的探测器，用于对反射X射线光子的计数.

2 结果与讨论

2.1 锌层厚度与光子注量的函数关系

将标准镀锌板测得的平均值根据MCNP程序的输入格式转换成厚度值后输入物理模型进行模拟，以获得标准镀锌板锌层的特征X射线荧光注量.分别在浪潮NX5760M3服务器、戴尔OPTIPLEX3010台式机、ThinkPad E450笔记本上运行MCNP程序，所得结果一致，证明仿真程序的平台无关性.Zn元素特征X射线荧光的能量范围是在1.009～9.657 KeV，故对光子计数器F2设置能量截断范围为1～10 KeV.表1所示为8组样坯的实验结果.

表1 8组样坯的实验数据Tab.1 Experimental data of eight different samples

表1中光子注量的物理意义为在1个光子参与的粒子输运过程中，能量范围为1～10 KeV时荧光光子通过1 cm2荧光探测器接收面的个数.由表1可知：锌层厚度与荧光光子注量呈正相关关系；相对误差呈下降趋势.相对误差的下降趋势也表明模拟较多数量的光子使光子真正的统计规律得以显现.由MCNP程序粒子运输过程计数和光子注量计数的误差均在置信区间内，故可以基于此数据进行曲线拟合绘制标准曲线.用标准板锌层厚度d值对荧光光子注量Φ作图，绘制了锌层厚度在7～20μm(单位面积质量在50～140 g·m-2)标准样品的标准曲线，如图3所示.所得标准曲线的相关系数为0.9992.所得标准曲线公式为：

Φ=-0.001d2+0.0389d+8.5269.

(3)

2.2 对比试验结果

取标准镀锌板同批次样坯7块，分别使用化学重量法、X射线荧光在线测量法、标准曲线法对样坯进行测量.重量法是一种通过化学方法溶解镀锌板锌层获得其单位面积的质量.重量法具有准确度高的优点，其测量值可作为近似真值.X射线荧光在线测量使用Thermo RM310EC在线涂层测厚仪.标准曲线法首先将重量法的实测值输入MCNP模型中计算其对应的光子注量，再从上述标准曲线直接得到它们的锌层厚度值.对比试验结果见表2.

图3 标准测量曲线Fig.3 Standard measurement curve

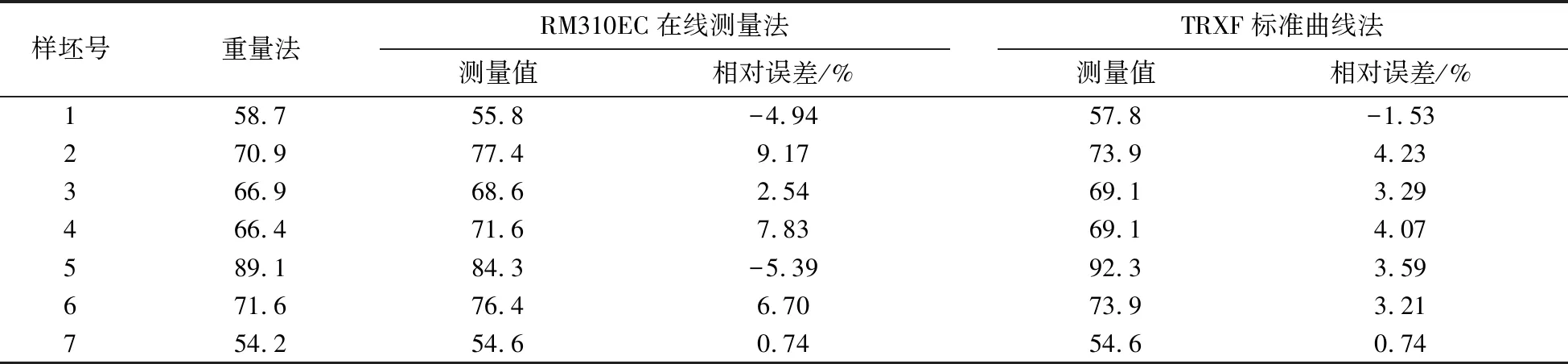
样坯号重量法RM310EC在线测量法测量值相对误差/%TRXF标准曲线法测量值相对误差/%158.755.8-4.9457.8-1.53270.977.49.1773.94.23366.968.62.5469.13.29466.471.67.8369.14.07589.184.3-5.3992.33.59671.676.46.7073.93.21754.254.60.7454.60.74

由表2可知：根据标准曲线得到的厚度值与重量法实测厚度更为接近，且相对误差不超过±5%，验证了标准曲线法的实用性.然而，在线测量数据可能出现偏差，在实际生产中必须采用离线测量方法核准锌层在线测量结果.因此，标准曲线法仍需要与离线测量方法对比验证其准确性.离线测量使用Rigaku台式荧光光谱仪.对比结果见表3.

表3 标准曲线法与离线测量对比试验(g·m-2)Tab.3 Comparison of standard curve method and off-line measurement(g·m-2)

由表3可知：标准曲线法的测量结果与离线测量法的相对误差基本小于±2%，满足在线测量值与离线测量值相差不超过±5%的要求，说明标准曲线法具有较高的准确性.由此得出图3中建立的标准测量曲线在7～20 μm的常规锌层厚度区间内是可以应用于镀锌板锌层测量的.

3 结论

1)本文构建的MCM模型通过了十项计数收敛统计检查，计算误差均在置信区间内，计数的过程和结果真实有效，说明物理模型能够有效的模拟TXRF技术的物理测量过程，验证了使用TXRF测量镀锌板锌层厚度的可行性.

2)通过比较上述物理模型的计算结果与多种测量方法实测值，标准曲线法测量结果更接近重量法测量真值，且与离线测量相对误差基本小于±2%，测量准确性较高，得到了在50～140 g·m-2的常规镀锌板锌层质量区间内的标准测量曲线.

3)镀锌标准板和标准测量曲线是在线锌层测厚的测量精度和准确性的重要保证，必须按周期使用镀锌标准板和标准测量曲线对在线锌层测厚仪进行检定或校准.本文建立的标准测量曲线作为在线测量的比对数据，为后续TXRF技术能够应用于在线测量创造了有利条件.