基于卫星编队的空间碎片视觉高精度导航方法
2019-04-04杨博王浩帆苗峻赵晓涛
杨博 ,王浩帆,苗峻,赵晓涛
1.北京航空航天大学 宇航学院,北京 100083
2.北京控制工程研究所,北京 100190
空间技术的快速发展使得空间碎片数量急剧上升,这些碎片对在轨航天器造成的威胁越来越大。截止2018年6月,美国通过地面检测编号的空间在轨物体数量已达19 125个,其中有效载荷4791个,空间碎片 14 334个[1],包括丢弃的设备、运载火箭末级、废弃的卫星、卫星和分级火箭分离时的碎片,以及航天器与原来空间碎片撞击产生表面材料剥落等[2]。随着人类航天活动的继续,空间碎片数量将持续增长。同时,碎片间的碰撞将产生更多小尺寸的新碎片[3-4],未来空间碎片数目呈指数增长趋势[5-6]。为保护在轨正常运行的航天器,需要对空间碎片进行高精度观测以进行抓捕、清除[7]。
目前,空间目标监视主要基于地基观测方式实现,美空军于2000年形成了完备的空间监视网[8],对于尺寸大于10 cm的碎片,可通过地基雷达、望远镜等对其进行观测。但地基观测方式在空间覆盖性、空间目标发现的及时性和空间目标认知等方面都存在局限性,难以满足空间攻防对空间目标信息的技术要求[9]。
与地基观测方式不同,天基观测具有探测范围广,不受地球大气、天气影响,覆盖范围广,探测精度高等优点[10]。美国建立了“天基空间监视”(SBSS)系统,目的在于部署能用于发现、识别和跟踪空间目标的光学传感器卫星星座,其最终目的是完全取代地基空间监视系统[11]。而常见的光学传感器中,单目相机因不能获得景深信息,必须辅助其它传感器,如激光测距仪等进行三维位置确定[12],而传统双目相机因基线较短导致观测精度低,只能用于近距离观测[13-15],文献[16]提出了编队飞行器可以构成长基线的观测系统,但没有进一步分析观测误差与编队卫星的关系,无法实现最优的编队构形。
本文基于双目视觉原理,采用卫星编队对空间碎片进行天基观测,不仅可以提高基线长度,而且通过多颗卫星的观测信息融合,可以大大增加观测视野,实现高精度观测。当一个航天器跟踪失败时,还可以利用其他航天器的观测信息进行导航,提高了系统的可靠性。
1 状态方程
描述目标相对运动的C-W方程为:

式中:ωT为主星的轨道角速度;fx、fy、fz为所受摄动力或控制力。

式中:

2 观测方程
利用卫星编队来建立观测方程,不仅可以增加基线长度,提高视觉传感器的探测精度,而且通过结合多颗卫星的观测信息,进一步提升了定位精度,扩大了观测范围,提高了观测可靠性。
2.1 双目观测原理
为了便于误差分析及简化计算,假定两个摄像机焦距相等,各内部参数相同,两个摄像机坐标系之间的距离为b,称为基线。图1所示为双目视觉测量模型,P点为由图像匹配算法检测并匹配成功的特征点,其在CL相机像平面上的点为P1,在CR相机像平面上的点为P2,则空间点P为CLP1和CRP2两条直线的交点,即而确定点 P 的三维位置[17]。

图1 双目视觉定位Fig.1 Binocular vision position
2.2 观测方程建立
(1)采用的编队构形
本文采用如图2所示编队构形,卫星之间可以基于信息拓扑结构对编队构型进行修正。根据自然编队构型以及拓扑结构关系,每颗卫星可根据其相邻两颗卫星传递的状态信息进行实时解算卫星之间的相对状态信息。

图2 采用的编队构形Fig.2 Formation configuration
以卫星2、3推导卫星1的运动状态为例,如图3所示。

图3 卫星2、3推导卫星1的相对几何关系Fig.3 Relative geometric diagram for satellite 1 deduced by satellite 2 and 3
在编队轨道坐标系中,由卫星2、3将自身状态信息传递给卫星1,卫星1进行实时解算,可得出卫星1相对于卫星2、3的目标位置矢量

式中:x、y为编队轨道坐标系 x、y方向单位向量;r为自然编队圆半径。
得到编队卫星之间的信息后,进一步观测空间碎片的信息。因光学探测无法得知空间碎片的构成而不能确定其质心,但由于大多数空间碎片尺寸较小,并且为了充分利用多个相机识别到的特征点的三维信息,可以将多个特征点的矢量加权假设为空间碎片的质心。由多个特征点构成的相对位置矢量R可表示为:

式中:ri为第i个特征点在参考坐标系中的三维坐标。
在编队卫星观测空间碎片过程中,每个小卫星携带一个双目相机,因此m个小卫星构成m个相机坐标系,利用多颗小卫星观测空间碎片的量测矢量如图4所示,有

式中:RT1为空间碎片在每个卫星参考坐标系下的估计相对位置矢量;Rk1为第k个从星在主星参考坐标系下的相对位置矢量;RTk为空间碎片在第k个卫星相机坐标系下的相对位置矢量;Mk1为相机坐标系之间的变换矩阵。

图4 量测矢量Fig.4 Observation vector
(2)编队观测方程
取状态变量为空间碎片相对于编队卫星参考坐标系下的位置RTk,将其直接作为观测量,则t时刻编队卫星对空间碎片的量测为:
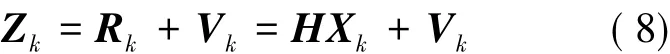

即Zk服从均值为Rk、标准差为σk的高斯正态分布。
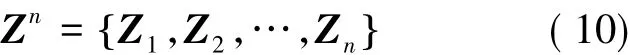
在目标当前位置(xi,yi,zi)条件下,测量值Zn的高斯概率密度模型可以表示为:

2.3 可观性分析
设^X为目标状态参量X的无偏估计量,由Cramer-Rao下界可知目标位置的估计误差协方差矩阵P与Fisher矩阵F的关系满足:

式中:
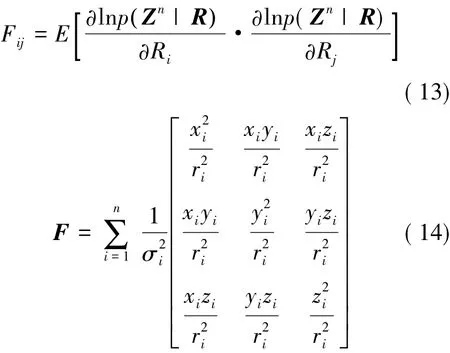
系统的估计误差方差阵及估计量的Fisher信息矩阵包含了系统的可观测信息,当F满秩时系统完全可观测,此时,估计误差方差阵P取得Cramer-Rao下界。由式(14)可知,Fisher信息矩阵满秩的条件为:

即观测航天器与空间碎片不能在同一条直线上,否则F矩阵是一个奇异矩阵,意味着系统状态参量中有一个或一个以上的分量是不可估计的,因此系统不可观测。
蛛丝从他的身体上空掠过,射在不远处的凸石上,像张开的五指,扒住了石面。随后,唐飞霄借着蛛丝的拉扯力,如飞天蜘蛛,倏地朝天葬师扑来。他那八足伸展起来,体长怕是已超过了两丈,而他与天葬师的距离,也不过才七八丈远,这一跃之间,便已到了近前,扬起钢钎一般的前足,朝着天葬师当胸插下!
还有一种情况为Fisher信息矩阵可逆,但具有大条件数ψ。正定矩阵的条件数定义为[18]:

式中:λmax与λmin分别表示矩阵的最大和最小特征值。大条件数矩阵意味着该矩阵是接近奇异的,即使此时矩阵可逆,但因为协方差矩阵的Cramer-Rao下界过大,系统估计量中会有一个或一个以上的分量存在较大的估计误差,观测性较差。
编队卫星对空间碎片观测的过程中,通常采用的编队构形不会使多颗小卫星与空间碎片位于同一条直线上,因此系统一定可观。在采用直线形编队时,编队卫星的连线应与空间碎片有一定的夹角,便能保证系统具有较好的观测性。
2.4 最优视差角设计
由图5中的坐标几何关系可得:

式中:(μ1,ν1)为空间碎片在左相机图像坐标系中的坐标;(μ2,ν2)为空间碎片在右相机坐标系中的坐标;Δγ=γ2-γ1为光轴指向与卫星连线方向的夹角。

图5 空间碎片观测几何Fig.5 Observation geometry of space debris
设相机参数相同,测量精度相同,分别为μ方向Δμ,ν方向Δν,则根据误差传递公式,特征点在追踪飞行器坐标系中的三维坐标间接测量精度为[19]:

式中:β1、β2为特征点视线方向分别在左右相机坐标系Oc1Xc1Zc1平面和Oc2Xc2Zc2平面内的投影与相应光轴方向的夹角;βγ为特征点视线方向在左相机坐标系Oc1Yc1Zc1平面内的投影与光轴方向的夹角,且有:

由式可知,观测过程中,像差偏差Δμ会在X、Y、Z方向分别产生Δx、Δy、Δz的误差影响,定义这个误差区域为误差立方体。在常用的双目相机模型中,基线一般为2m左右,这在远距离观测中会造成上百米量级的误差立方体,限制了双目相机的使用,而提高基线长度会对航天器直径提出过高要求。采用如图2所示的观测构形,首先由卫星1和2组成双目视觉模型观测得到空间碎片的图像信息,由卫星3和4组合成双目视觉模型得到空间碎片的另一图像信息,在卫星1和和卫星3上分别解算出空间碎片的位置信息,产生的误差立方体在XOZ面的平面图如图6所示,A1B1C1D1为卫星1解算得到的误差立方体,A2B2C2D2为卫星3解算得到的误差立方体,阴影区域为两颗小卫星观测的重叠区域,若每颗卫星都能正确识别到目标,则目标的位置必在这个重叠区域内。由此可知,利用编队卫星可以缩小观测的不确定区域,提高观测精度。
由图6可以看出,误差区域的缩小与两航天器与空间碎片形成的夹角有关,定义这个角为视差角θ。误差立方体重叠的区域会随着视差角θ的变化而变化,定义重叠区域的体积与原误差立方体体积的比值为缩小率,利用蒙特卡洛法仿真106次,得到误差立方体的缩小率与视差角的关系如图7所示。

图7 误差立方体缩小率与视差角之间的关系Fig.7 The relationship between the error cube reduction ratio and the parallax angle
由图7可知,当视差角为90°时,误差立方体最小,观测精度最高,但当视差角在60°~120°时,精度变化不是很明显,因此在工程实现中,只要保证两航天器与空间碎片的视差角在60°~120°,即可保证量测精度提高90%以上。
由以上分析可得,卫星1、2的量测信息在卫星1的相机坐标系中解算出目标空间碎片的位置信息,卫星3、4的量测信息在卫星3的相机坐标系中解算出目标空间碎片的位置信息,再由卫星1、3通信,对目标空间碎片进行高精度定位。当卫星1与卫星3的视差角在60°~120°,即卫星1的光轴与卫星3的光轴在60°~120°时,可以保证量测精度提高90%以上。
3 相对导航仿真
为验证利用编队小卫星观测空间碎片的可行性,利用EKF进行数值仿真。假设空间碎片轨道高度700km,轨道周期2 h,离心率为0。相机参数如表1所示。

表1 可见光相机参数Table 1 Visible light camera parameters
在上述仿真初始条件下仿真2000s,视差角θ=90°,分析利用传统基线b=2 m的一颗卫星观测以及b分别为100m和1000 m的编队小卫星观测时的误差,如图8所示。

图8 基线b=2m单颗卫星导航误差(传统方法)Fig.8 Navigation error by single satellite when the baseline is 2m(traditional method)
由仿真图可以看出,编队卫星可以增加基线长度,提高观测精度。图8为单颗小卫星观测时的导航误差,由于基线较短,三轴导航位置误差为较大,如表2所示。图9为基线b=100 m时编队卫星观测的导航误差,可以看出编队观测减小了三轴误差,提高了导航精度。图10为采用基线b=1km时编队卫星观测的导航误差,可以看出导航精度进一步提升。

表2 导航精度仿真Table 2 Navigation accuracy simulation m

图9 基线b=100m编队卫星导航误差Fig.9 Navigation error by satellite formation when the baseline is 100m

图10 基线b=1km编队卫星导航误差Fig.10 Navigation error by satellite formation when the baseline is 1km

图11 视差角为30°时导航精度仿真Fig.11 Navigation accuracy simulation when θ=30°

图12 视差角为60°时导航精度仿真Fig.12 Navigation accuracy simulation when θ=60°
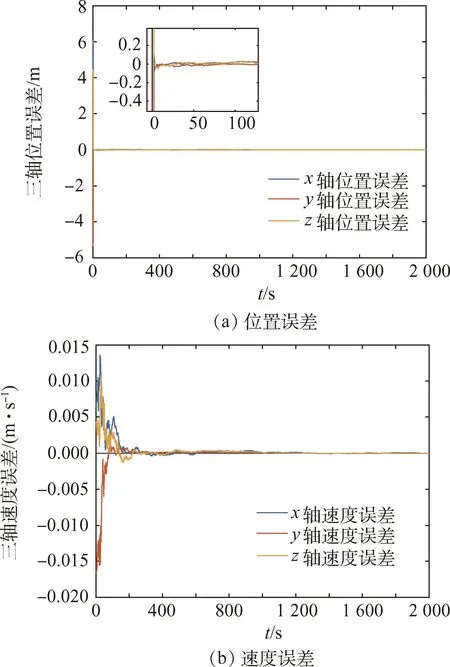
图13 视差角为120°时导航精度仿真Fig.13 Navigation accuracy simulation when θ=120°

表3 导航精度仿真Table 3 Navigation accuracy simulation m
4 结束语
本文研究了利用卫星编队对空间碎片进行导航定位的问题。
1)针对空间碎片非合作的特性,采用视觉传感器进行导航,建立了误差模型,设计了最优视差角,实现了利用卫星编队对空间碎片进行高精度导航定位;
2)分析得出当不同卫星之间的视线夹角为90°时由观测量融合得到的误差立方体最小,导航精度最高,但在工程实践中达到60°~120°即可保证足够的精度;
3)仿真验证了当编队卫星之间的距离为1km,视差角为90°时,定位误差可以达到0.1 m的量级。
本文方法不仅提高了导航精度,而且扩大了观测范围,增加了观测系统的可靠性。由于编队小卫星的广泛应用,本文方法易于工程实现。
