存储器抗辐射加固的矩阵纠错码研究
2019-04-04施宇根李少甫齐艺轲
施宇根,李少甫,2,* ,齐艺轲
1.西南科技大学 信息工程学院,绵阳 621010
2.中国空气动力研究与发展中心 气动噪声控制重点实验室,绵阳 621900
集成电路芯片是航天技术发展的基石,随着大规模集成电路的高速发展,高精度的制造技术和小型化的器件使得更大规模集成电路占据更小的面积[1]。但在辐射环境中,各种高能粒子(重粒子、质子、中子、α 射线等)[2]会对电路造成严重的破坏,电路的可靠性甚至电子设备的正常工作都受到了严重影响。辐射粒子对集成电路造成的影响可大致分为总剂量效应(Total Ionizing Dose,TID)和单粒子(Single Event Effects,SEU)效应[3-4]。其中不会对电路造成持久影响的错误被称为软错误,相应的辐射粒子对电路造成永久不可恢复的错误称为硬错误。而一般软错误是影响电路可靠性的主要因素[5-6]。
自20世纪70年代以来,根据美国国家地球物理数据中心(National Geophysical Data Center,NGDC)统计,空间辐射效应是使得航天器发生故障的主要因素。同时存储器在一个芯片中占据了30%的面积,而在集成电路系统级芯片(SoC)中存储器所占面积更是超过了60%[7],且存储器失效相对于逻辑门更加敏感,存储器的可靠性成为航天器正常工作的关键一环。
集成电路加固技术主要有工艺级、电路级、版图级和系统级加固。在系统级加固方面,汉明码作为一类典型的单纠错双检错(Single Error Correction-Double Error Detection,SEC-DED) 编码[8]被广泛应用并衍生出了许多改进方法,例如最小列奇重量编码[9]减小了码字重量使得该纠错码相对于汉明码提升了可靠性并减少了功耗。
集成电路中各单元之间的距离变小使得单粒子事件发生多位翻转的概率增加,为此许多学者开始了探索纠正存储器的多位翻转的纠错方法,内建电流探测器(Built In Current Sensors,BICS)[10]结合SEC-DED或奇偶校验码对存储器进行纠错,该方法对硬件结构进行调整,减少冗余位同时纠正多位错误;矩阵码(Matrix Code,MC)[11-12]在其每一行使用汉明码,而每一列使用奇偶校验码,使得纠错码在低功耗的情况下有更高的覆盖率,同时可以纠正2位错误;二维纠错码[13]针对单个码字构造出了可纠错多位错误的低复杂度检错和纠错电路;修正矩阵码(Modified MC,MMC)是对矩阵码的改进[14],多次迭代后可以100%检测3位错误;低冗余位矩阵纠错码[15]以增加编译码复杂度的条件到达减少冗余位,纠正多位错误的目的;十进制矩阵码(DMC)[16]针对单个码字有着很强的纠错能力。但在空间辐射环境中,随着电路单元尺寸越来越小,存储器发生多位翻转的概率越来越大,所以需要具有更大纠错能力的加固方法对存储器进行加固。
本文研究的矩阵纠错码使用较少的冗余位,可以有效的对存储器多位翻转进行加固。首先,本文将存储器的字在逻辑上划分为多个4阶矩阵,并将矩阵划分成相互联系的3个区域,根据划分的区域提出了一种矩形循环校验的方法构造校验位。随后,设计了译码算法和译码电路,研究的矩阵纠错码可以纠正数据宽度为5的连续翻转或者不连续翻转。最后,根据校验位构造检测位以减少硬件开销,运用版图分割法[13]排列数据的输入的逻辑顺序确保了冗余位发生翻转时不会影响存储器的可靠性,进一步提高了矩阵纠错码的性能。
1 矩阵纠错码
本文研究的矩阵纠错码使用较少的校验位获得了较强的纠错能力。以数据宽度为16bit的字为例,图1将一个16bit位宽的码字在逻辑上构造为一个4阶矩阵。并且将该矩阵划分为3个区域,数字相同的位置按如下公式构成矩阵的校验码:


图1 数据宽度16位的纠错码Fig.1 Error code for 16-bit data
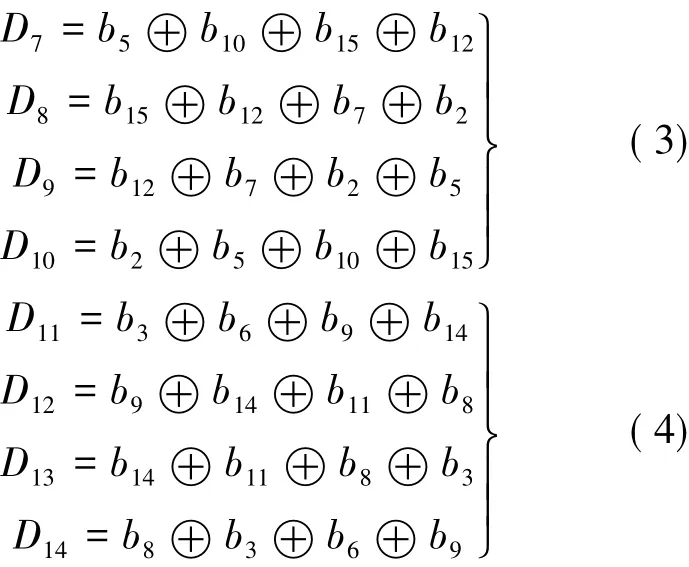
式中:bi为第 i个初始信息位,i∈ (1,2,…,16);Dk为第k个得到的校验位,k∈ (1,2,…,14)。
运用矩形循环校验法构造公式(3)(4)。具体构造方法如图2所示,图中的信息位按照逆时针(1,3,5,6;5,6,4,2;6,4,2,1;2,1,3,5)顺序得到4个校验位。表1给出了16个状态表示的64种翻转情况,列出了最多4bit翻转的出错状态。然后通过指定数据宽度以及迭代运算使翻转状态和翻转情况从一对多转换为一对一。

图2 信息位的循环校验示意Fig.2 Illustration of circular parity of information bit
使用矩阵纠错码对码字的连续多位翻转进行纠错,纠正算法可以对数据宽度为5的信息位的连续或不连续翻转进行纠正。对初始的信息位按式(1)~(4)进行编码后,依次得到校验位Dk。接收数据位后,译码步骤可以表示为以下几步:

2)首先根据S1~S6对图1(b)中的1区翻转位进行纠错,同时根据S1~S4、S7~S14结合表1对2区进行纠错。b1和b7分别为1区和2区的数据位,其纠正公式如下:

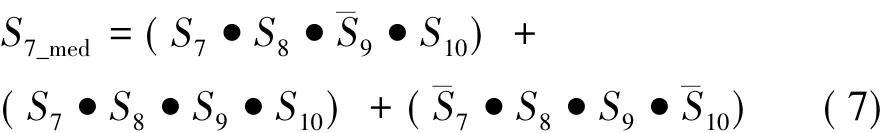
其中S7_med遍历了数据宽度为5位时b7的翻转情况对应的翻转状态,珔Sk表示取反,
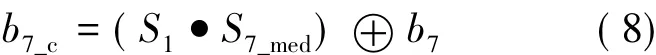
所以1区和2区的纠正公式可描述如下:

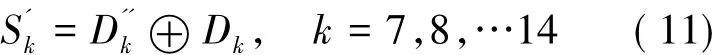
进行迭代后图2中的3、4位将被确定正确,因此在指定数据宽度后,出错的情况大大减少。
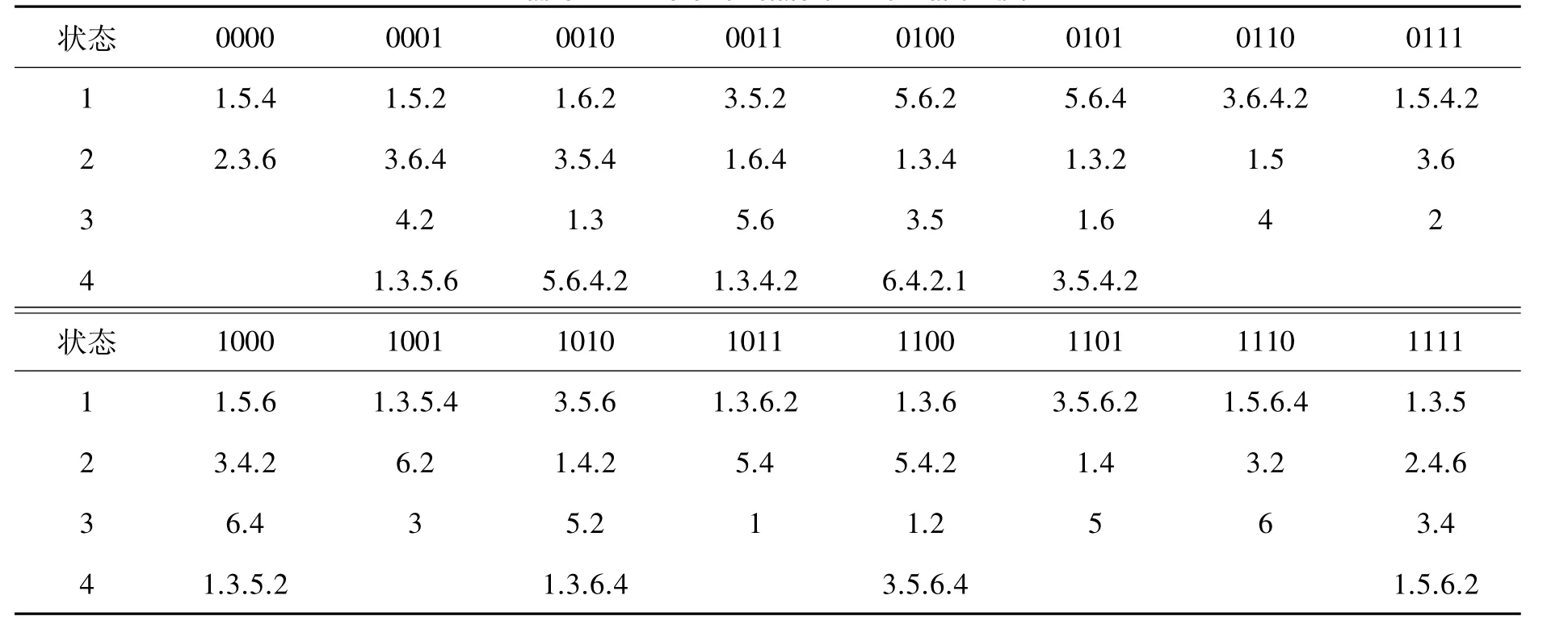
表1 信息位的出错状态Table 1 The error state of information bit
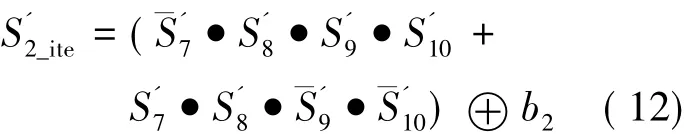

所以3区的纠正公式可以表示为:
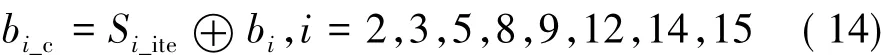
3区纠正完成后算法结束。对图3中的翻转位首先通过公式(6)对纠正b1,通过公式(15)纠正b4:

迭代后通过式(12)~(14)对3区翻转位进行纠正,此时纠正算法完成:


图3 翻转位位置示意Fig.3 Illustration of the location of error bit
2 矩阵纠错码的电路设计和数据排列
2.1 译码器电路设计和纠错能力验证
译码电路接收校验位Dk和信息位bi,产生,图4给出了部分译码电路结构:1区进行纠正后直接输出;2区的纠正在输出的同时还要作为3区的输入;3区接收2区纠正位重新产生校验位完成纠正。使用FPGA对电路进行功能验证,图5是模拟其中一种翻转情况的纠正测试结果,译码电路完成了对信息位5位数据宽度翻转的纠正,其中D_in1表示式(1)(2)的检验位输入,D_in表示式(3)(4)的检验位输入。
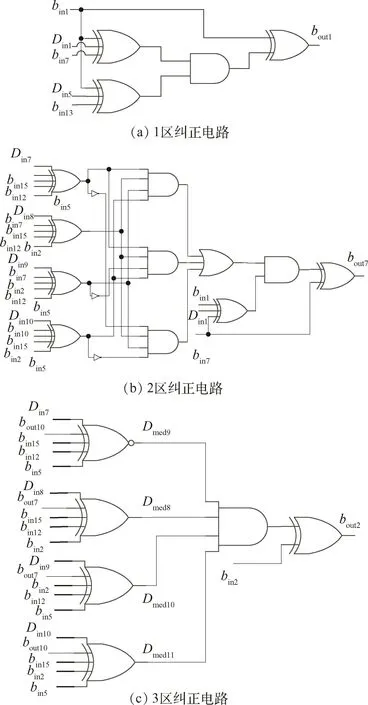
图4 研究的矩阵纠正码译码器电路设计Fig.4 Decoder circuit for proposed matrix error code
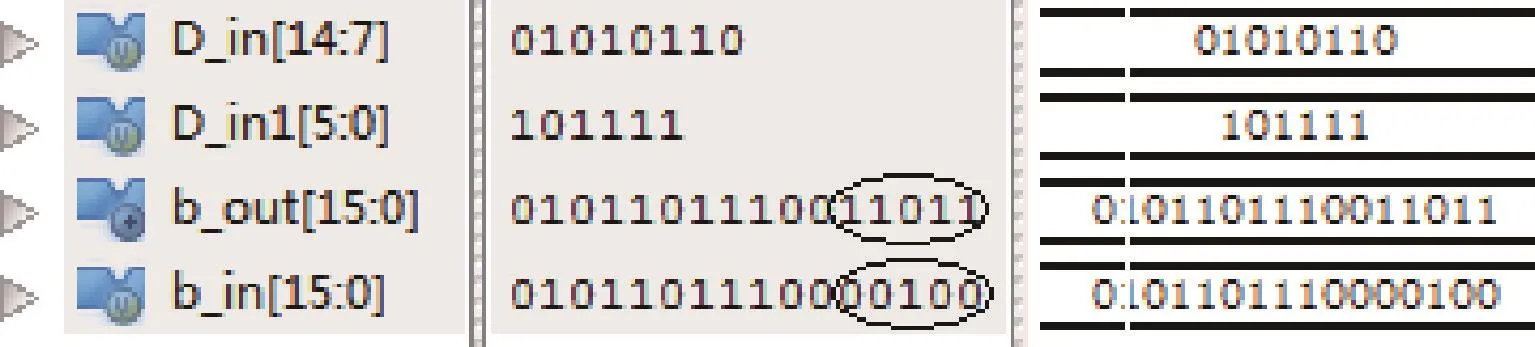
图5 数据位出错模拟纠正结果Fig.5 Simulation correct result for error data
2.2 矩阵纠错码的检测位构造和数据排列
为了使得所研究的矩阵纠错码有更好的可靠性,需要考虑冗余位出错时是否会影响。所以除了需要考虑数据位翻转外,还要考虑冗余位发生翻转以及校验位和冗余位同时发生翻转的情况。当某些校验同时发生错误时,研究的矩阵纠错码电路将不能对信息位进行准确纠正,例如D1和D5同时出错时,对1区中的b1错误纠正;D1,D8,D9同时出错时,2区中的b7将会被错误纠正;迭代后3区中的错误与状态唯一对应,当相应的校验位出错时,3区中的信息位会被错误纠正。
文献[13]提出了一种“版图分割法”,其利用存储单元的版图结构,在逻辑输入过程中有选择性的存放数据。图6为校验位的排列方式,其确保了表1中出错状态和出错情况唯一对应,同时避免了某些校验位同时出错,使得电路能得到简化。右边8个校验位作为检测位,与数据位间隔1个无效位。当发生翻转的数据宽度为5位时,检测位可以100%检测出错误,降低了电路的硬件开销。图7为数据位的实际逻辑输入。图8为检测位数据宽度为5位的其中一种冗余位翻转情况的模拟纠正结果,其中D和D1为正确的冗余位,D_C和D_C1为翻转的冗余位。使用MATLAB对信息位以数据宽度5 bit为单位,顺序注入随机错误1 000次,确定冗余位(仅检测位)翻转以及信息位和冗余位同时翻转的最大翻转情况,以此对译码算法进行功能验证的结果如表2所示。

图6 冗余位排列方式Fig.6 The layout of parity bit

图7 一个16位宽度数据的实际逻辑输入Fig.7 A 16-bit data of memory actual logical input

表2 错误注入结果Table 2 The result of injecting error

图8 冗余位出错模拟纠正结果Fig.8 Simulation correct result for parity bit
3 试验和分析
本节对所提出的矩阵纠错码的纠正能力和电路性能进行分析,并分别对性能优异的矩阵码[12]和二维纠错码[13]进行电路性能估计和可靠性分析,以此来进行比较。
3.1 纠错码的可靠性分析
平均失效时间(MTTF)是衡量存储器可靠性的一项关键指标,可以通过计算MTTF来大致分析存储器的可靠性。存储器多位翻转的MTTF准确计算模型[17]如下:

式中:λ为粒子到达率;M为存储器字数;N为信息位和冗余位总位数;L为纠错能力;pipj为超过纠错能力L的概率,pi和pj服从泊松分布。假设粒子到达率 λ 为 10-4,MBU=5,通过式(19)计算后,图9给出了存储器字数和MTTF的关系,本文研究的矩阵纠错码的可靠性是3种纠错码中最高的。
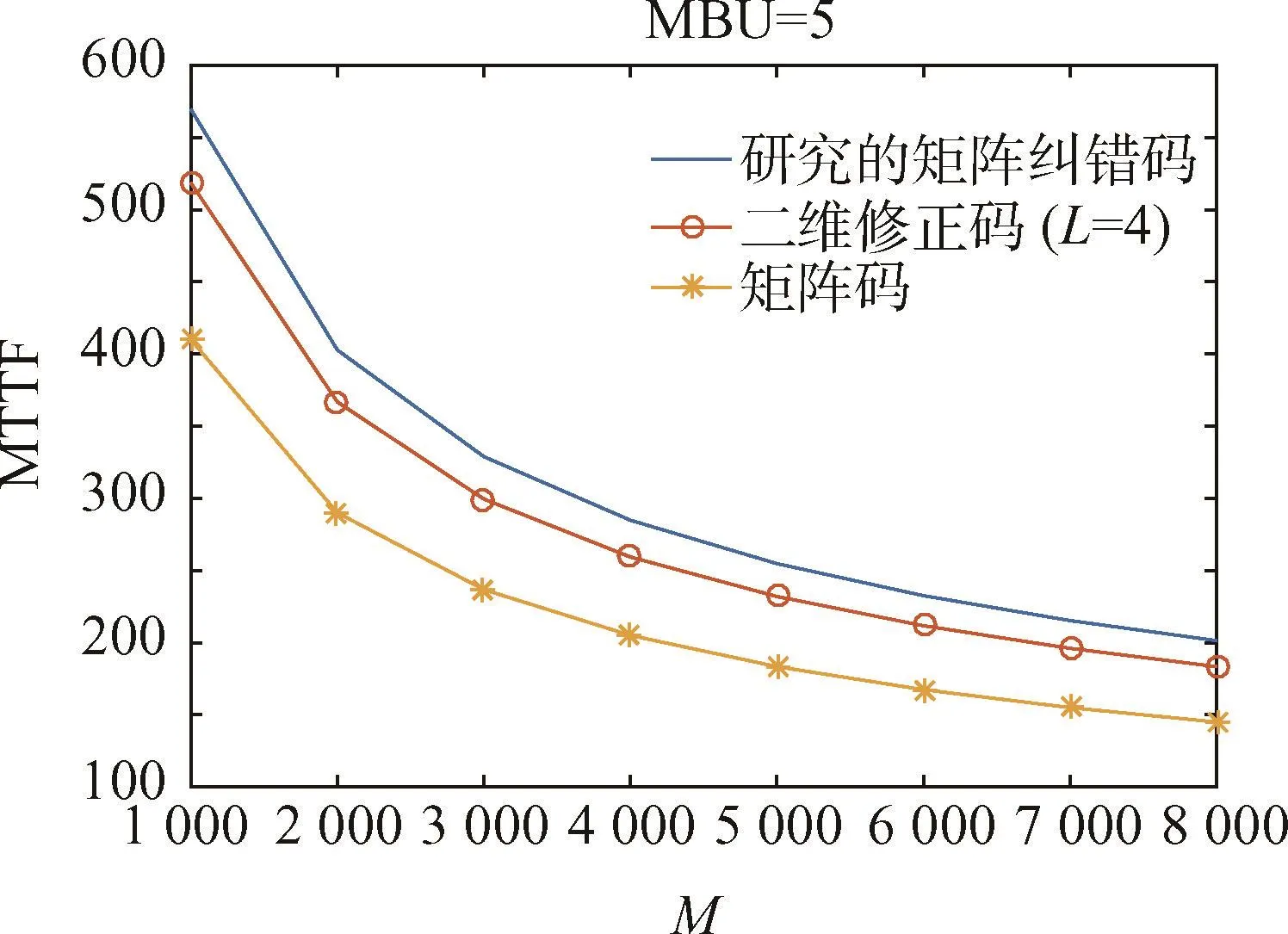
图9 存储器的MTTF与字数关系结果Fig.9 The result figure of MTTF versus M for a 16-bit memory
3.2 译码电路性能分析
使用0.18 μm工艺库估计3种纠错码的功耗,时延和面积参数。使用Design compiler综合工具对电路进行综合。性能参数结果如表3所示,所研究的矩阵纠错码使用更少的冗余位获得了更好的纠正能力。其中表3中后两种码字为32位宽度,十进制矩阵码(DMC)[16]在 32位码字中可以100%纠正数据宽度为5位的数据,同时构造了编译码共用的电路大大减少了硬件开销;校验位共享纠错码[15]可以纠正数据宽度为4位的数据,同时其对得到的校验位进行二次编码,以增加电路复杂度为代价,减少了校验位。
本文研究的矩阵纠错码由于电路译码时需要进行一次迭代,使得电路有较高的时延。
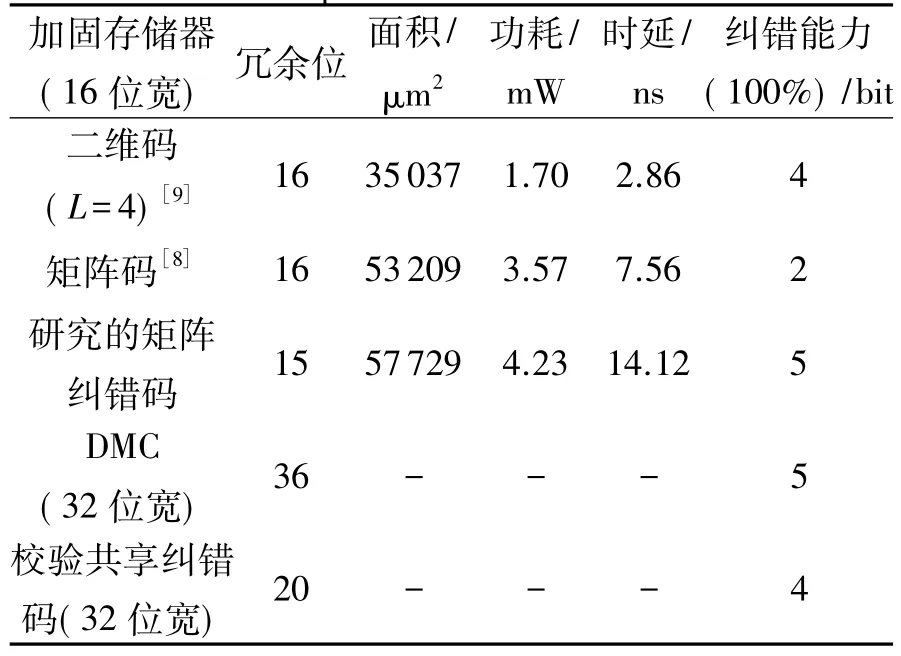
表3 纠错码性能表Table 3 The performance of error code circuit
4 结束语
本文研究的矩阵纠错码,使用较少的冗余位更好地完成了存储器抗多位翻转加固,结合版图分割法使得指定数据宽度的冗余位发生翻转不影响存储器的可靠性。所设计的纠正电路的纠正性能优于目前已知的多位纠正电路,但电路具有较高的时延。综上所述,纠正电路适宜于辐射环境下对冗余位和可靠性需求较高的存储器。
