巧借直观表征促进学生思考

2019-04-04陈双雅

名师在线 2019年8期

陈双雅

（福建省晋江市实验小学，福建晋江 362200）

引言

数学直观从表征方式来说，一般包括几何直观、符号直观和模型直观三种。几何直观是指依托、利用图形进行教学的思考和想象，本质上是通过图形展开的想象能力。也就是说，将数量关系用几何图形进行表示，通过直观观察以达成认知的目的。符号直观是指借助符号来直观表征，是描述数学对象、数量关系以及规律的一切符号，还包括文字、图表。模型直观是指将一些抽象的数学概念通过生活经验来呈现出来。

几何直观是《义务教育数学课程标准(2011年版)》提出的十个核心概念之一，主要是指利用图形描述和分析问题。借助几何直观，可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。在小学数学教学中，教师要尽可能地借助直观表征帮助学生更好地进行数学学习，以提高学生的数学素养。

一、在知识的起点处，直观形象促进思考交流

数学是一门训练思维的学科，数学教师要教会学生思考。直观形象的图像有利于促进学生通过观察与思考，深刻地体会抽象的数学知识本质，激发学生从具体现象中对比、发现并概括出抽象的数学知识，让学生在思考、交流中梳理知识[1]。

例如，在学习《分数的意义》时，把单位“1”平均分成4 份，表示其中的1 份。单位“1”形状不同，平均分成4 份后，每一份的形状、大小看上去都不同，为什么都可以用四分之一来表示呢？把一个饼平均分成4 份，把一张长方形的纸平均分成四份，把一条线段平均分成4 份……让学生利用直观图形来观察、分析，发现它们都有着本质上的共同点——尽管图形形状、大小不同，但是都是把它平均分成4 份，其中的一份就是表示它的四分之一。

这样借助直观，让学生经历观察、互动交流，在对比分析中把握知识的本质，将复杂、抽象的分数概念变得形象、具体、可视化，使数学思考走向深处。

二、在思维的节点处，直观形象促进体验建构

在探索数学知识的过程中，只有让学生通过观察、实验、分析、抽象、概括等活动经历数学知识的形成过程，感悟其蕴含的数学思想方法，才能使学生掌握的知识是鲜活的、可迁移的，学生对数学知识的理解才能到位。有意识地渗透一些基本的数学思想方法，可以加深学生对数学概念、公式、定理、定律的理解。教师可以借助直观表征，培养学生分析问题、解决问题的能力，从而提高学生的数学能力和思维品质。小学生对抽象的、理论性强的知识理解力不足，受思维和知识储备的限制，他们对抽象的数学概念、性质、定律等的学习常常感到力不从心，很难从抽象中直接去概括、去获取，要么不理解，要么一知半解，往往将概念、性质的表面内容死记硬背地留在记忆层面，而这种认识是很难长时间记忆的。因此，在教学过程中，借助直观表征帮助学生理解显得尤其重要[2]。

例如，在学习“平行四边形的面积的推导”时，有了长方形面积知识作铺垫，让学生动手操作。大部分学生沿着平行四边形底边上的高剪开移到另一边，使它形成一个长方形，然后再通过拼成的长方形与平行四边形面积不变的关系，分析出平行四边形的底相当于长方形的长，高相当于长方形的宽，所以平行四边形的面积=底×高。

三、在思维的拐点处，形象直观促进思想感悟

（一）在迷雾处现直观，唤醒无序思维

在数学学习中，学生难免会遇到困惑，教师可以利用多媒体将直观的图形结合展现在学生的跟前，让他们眼前一亮，及时调整找准切入点，深入思考，有序探索。

例如，在教学五年级上册第二单元《轴对称和平移》时，如果教师直接将教学内容呈现给学生，学生很难将轴对称的形象特征联系起来。因此，利用动态的多媒体直观形象地将生活中的美丽的轴对称图案呈现出来，把它们变得形象、直观、生动、有趣，并将其融入课堂教学中，使其成为学生探求新知的有效辅助工具，有助于激发学生探究知识的意识和欲望，引发其深入思考。

（二）在数形中现直观，帮助分析理解

在小学数学中，由于学生受知识基础和具体形象思维特点的限制，因此教材对一些数学概念、公式、定理、定律等进行加工，借助直观表征将抽象的数学性质用具体、直观、形象的方式展示出来，以帮助学生更好地理解。

例如，在学习《分数的基本性质》时，将抽象的规律性的知识化为直观、形象的图形，如把一个长方形看作单位一，平均分为两份，占一份是1/2（见图1），平均分成四份，占两份是2/4（见图2），平均分成八份，占四份是4/8（见图3）。

图1

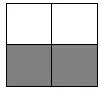
图2

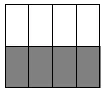
图3

平均分的份数和取的份数不断发生变化，而什么始终不变呢？学生通过观察、分析、归纳、总结，得出原来分数的分子和分母同时乘以或除以相同的数，阴影部分的大小始终不变，说明分数的大小不变。紧接着再次完善，归纳出“分数的分子和分母同时乘以或者除以相同的数，分数的大小不变”的规律。

又如，在学习《相遇问题》时，教师可以利用画线段图来帮助学生分析和理解题意。“淘气家到笑笑家的路程是840米，两人同时从家里出发，淘气步行的速度是70米/分，笑笑的速度是50米/分，两人经过几分钟相遇？ ”

学生初次理解两人1 分钟合走一段路程是有些困难的，而对1 分钟单独走的距离比较容易理解。基于这样的分析，笔者在教学中采用直观动态化线段图的方式来进行展示，学生不难发现淘气和笑笑每分合走120米，而840米里面含有几个120米就是两人几分钟相遇。这样，学生很快就领悟了其中的奥秘，问题便迎刃而解。

（三）在探究中现直观，引导自主思考

数学课堂必须紧扣数学之“魂”，以探促“思”。有了思维的数学课堂才是有灵魂的课堂，学生在这样的课堂上思维才能变得更敏锐、更理性。当然，小学生数学的思维训练，不仅要关注计算结果是否正确，还应关注计算的思维过程是否最优化，通过优化思维过程，探寻最佳的思维方式。

例如，在学习《变化的量》时，笔者利用多媒体出示小明1～6 岁的体重变化情况，利用图表直观展示，采用小组合作探究方式，并在小组内用这样的话来描述：“年龄在变化，体重也在变化”“年龄在增加，体重也在增长”……在形象直观的图示指导下，学生自觉、自主地体验感悟，发现体重随着年龄的变化而变化，一种量变化，另一种量也随之变化，但是此变化不成规律，也就说明年龄和体重是不相关联的两种量。判断两种量是否成正反比例，首先就要判断它们是否是相关联的量？两种相互变化着的量是认识正反比例最关键的节点，也是今后学习函数的起始点。有些量看似成正反比例，可恰恰它们是不相关联的量，学生不易判断，易产生混淆。例如，错误观点：判断明明上学所走的路程，随着明明体重的变化而变化。分析：明明上学所走的路程和明明的体重不是相关联的量，路程不会随着体重的变化而变化。借助直观，理解变得轻松、浅显。