巧解第35届预赛中的抛体问题

李志雄

(莆田第十中学,福建 莆田 351146)

1 第35届全国中学生物理竞赛预赛中的抛体问题

第35届预赛第6题:田径场上某同学将一铅球以初速度v0抛出,该铅球抛出点的高度为H．铅球在田径场上的落点与铅球抛出点的最大水平距离为________,对应的抛射角为________．重力加速度为g．

2 解法探讨

这是一个与生活实际直接相关的经典问题,在许多物理竞赛类的教辅书中都有此问题的解答,一般是以时间t为参数,从运动方程出发来计算,这种解法思路自然,但计算复杂．下面利用中学数学技巧给出2种简捷的解法,从中能使人体验到数理结合的科学美．

2.1 利用柯西不等式

(1) 柯西不等式简介.

柯西不等式是目前高中数学选修4-5中的内容,但不如均值不等式一样为物理教师所熟悉,下面先从平面向量的背景介绍二维形式的柯西不等式．

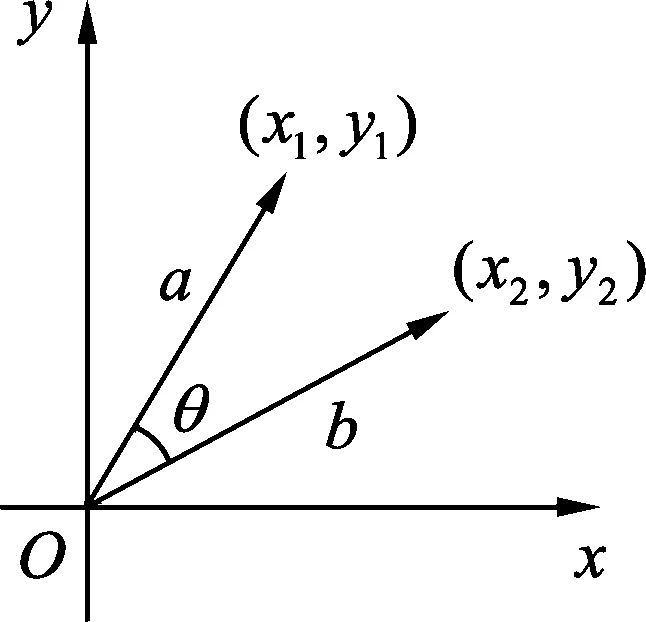
图1

如图1所示,设在平面直角坐标系中有向量a=(x1,y1),b=(x2,y2),a与b之间的夹角θ,根据向量数量积的定义有

a·b=|a||b|cosθ.

(1)

因|cosθ|≤1,所以有

|a·b|≤|a||b|.

(2)

用平面向量坐标表示(2)式,得

(3)

(2) 分析与解答.

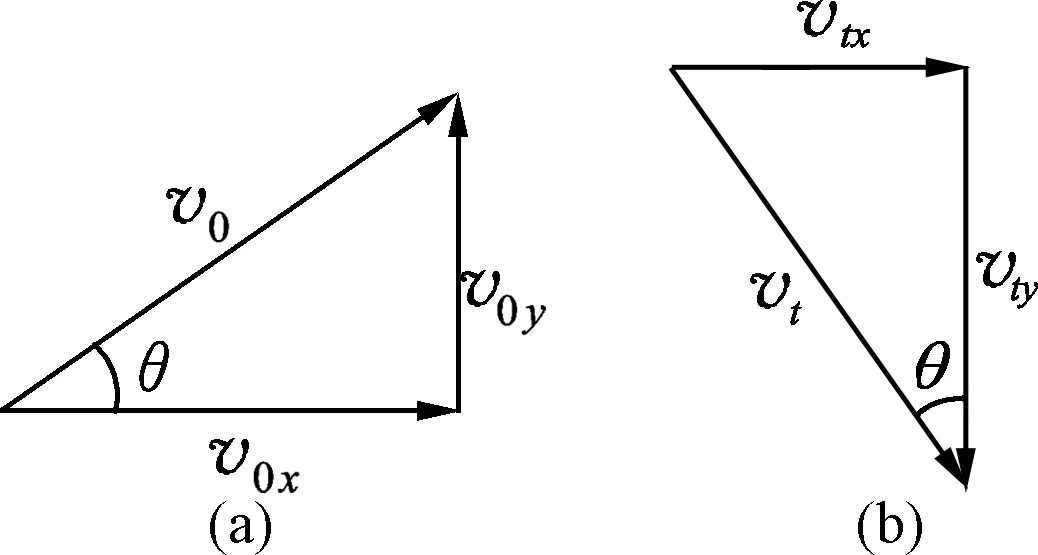
图2

(1)

落点与铅球抛出点水平距离为

x=v0xt.

(2)

由(1)、(2)式得

(3)

注意到v0x=vtx,将(3)式变形,利用柯西不等式有

即落点与铅球抛出点的最大水平距离为

根据柯西不等式取极值时的条件,抛得最远时有

则图2(a)和图2(b)中2个速度矢量三角形相似,设此时抛射角为θ,有

2.2 利用矢量三角形

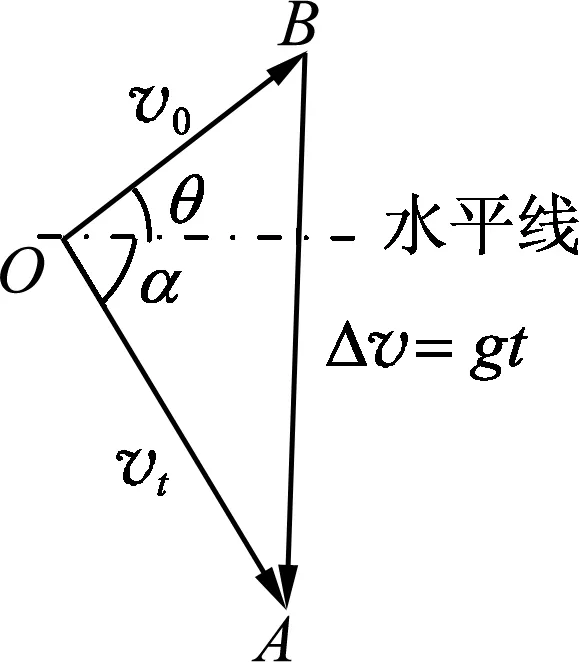
图3

如图3所示,初速度v0、落地时末速度vt、速度改变量Δv构成矢量三角形OAB,设抛射角为θ,末速度vt方向与水平线夹角为α,注意到Δv大小为gt,矢量三角形面积为

(1)

落点与铅球抛出点水平距离为

x=v0cosθ·t.

(2)

由(1)、(2)式可得

(3)

由(3)式知,只要使三角形OAB的面积S最大,水平射程x就能达到最远,而此矢量三角形的

面积也可用正弦公式表示为

(4)

因v0、vt大小都是确定的,由(4)式知,要使面积S最大,应使sin(θ+α)=1,即θ+α=90°,此时,由(3)、(4)式有

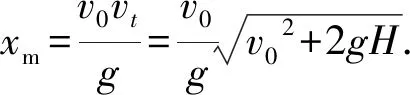
因OAB是直角三角形,有