Zernike多项式的条纹反射三维面形重建算法研究
2019-04-02田爱玲聂凤明刘丙才刘卫国
韩 路,田爱玲,聂凤明,刘丙才,刘卫国
(1.西安工业大学 光电工程学院/陕西省薄膜技术与光学检测重点实验室,西安 710021;2.中国兵器科学院宁波分院,宁波 310022)
随着光学反射镜制造技术在民用、军用及航空航天等领域的加速发展,大口径镜面物体的面形检测需求越来越大。现有的光学三维测量技术主要针对漫反射表面[1-2],难以有效地测量镜面物体。条纹反射法作为一种结构简单,动态范围大,测量精度高,检测速度快,同时无需其他辅助元件便可实现对任意形状镜面进行检测的方法[3-5],越来越受到国内外相关学者的关注。
从离散的梯度数据到面形高度需用三维面形重建算法进行恢复。面形重建作为条纹反射镜面测量研究的一个关键步骤,其重建精度直接影响最终的测量精度。传统的基于梯度数据的面形重建算法主要包括三种:十字路径法、傅里叶变换积分法以及区域波前重建法[6-8]。其中,十字路径法操作简单,速度快,但抗噪性差,面形恢复精度不高;傅里叶变换积分法是一种全局积分方法,对大数据量梯度重构速度快,但边界数据需满足周期性延拓条件;区域波前重建法理论上可以对任意形状的面形进行拟合,但计算量大,速度慢。目前,条纹反射面形重建中,主要以傅里叶变换法和Southwell区域波前重构法的应用最为广泛。文献[9-10]通过仿真模拟分析了经由梯度数据重建三维面形的主要算法,并对其重建精度进行了对比研究。结果表明,区域波前重构法不但对高频噪声有较强的抑制作用,同时也可以处理复杂的连通区域和非等间距分布梯度数据的复杂情况,但该方法在求解过程需消耗大量的时间,限制了其在快速实时测量系统中的应用;文献[11-12]基于泰勒定理提出了一种具有高阶截断误差的积分算法,并通过仿真实验验证了该方法在提高重建精度方面的有效性。该方法在研究微小形变区域时重建精度较高,但当表面有空洞时,积分时间较长;文献[13]通过引入迭代补偿,对传统的最小二乘二维积分方法进行了改进,解决了由于Southwell网格模型不完备而导致重建不准确的问题,有效提升了积分重建精度,但其处理时间会随着迭代次数的增加而线性增长;文献[14]采用高效、稳定的超松弛迭代法对Southwell模型积分重建进行了优化,提高了积分精度,但该方法的广泛应用需依赖先进的超松弛迭代算法。以上研究主要对传统的重建方法进行了分析和完善,以提高运算时间及优化测量精度。条纹反射法的误差主要来源于系统标定,引入的面形偏差主要为低频面形偏差,传统的基于梯度数据的三维面形重建方法均无法给出像差系数。而Zernike多项式面形拟合法[15-17]可以通过去除低频面形偏差对高频信息进行误差分析以提高条纹反射面形重建精度。
Zernike多项式面形拟合是由Fritz Zernike在1934年第一次提出[18],作为一种常用的光学波面拟合方法,其具有较高的拟合精度,在整个面形重构过程中具有重要的地位。由于该多项式由一系列在单位圆内相互正交的多项式基构成,与在光学系统中观测到的像差具有相同的形式,因此可以有效地描述波前参数。Zernike多项式对光学问题中有关波面的拟合精度最高,且本身的旋转对称性使得光学问题的求解具有很好的收敛性。传统的 Zernike 面形拟合方法主要是将离散的面形数据采用 Zernike 多项式的方式拟合成光滑连续面形。本文针对传统条纹反射三维面形重建算法无法给出像差系数的问题,提出了一种基于Zernike正交多项式的梯度数据面形重建方法。利用Zernike多项式中每一项与光学系统中波像差一一对应的关系,在获得面形重建结果的同时准确地给出初级像差系数。在建立数学模型的基础上,利用计算机模拟仿真的方法,以连续光滑双曲面为例进行算法的有效性验证。
1 条纹反射面形重建理论
1.1 条纹反射基本原理
条纹反射检测法是基于简单的光线反射原理,理论上可实现对任意形状镜面的面形检测。系统结构如图1所示,分别由液晶显示屏(Liquid Crystal Display,LCD)、相机(Charge Coupled Device,CCD)和计算机(Personal Computer,PC)组成。
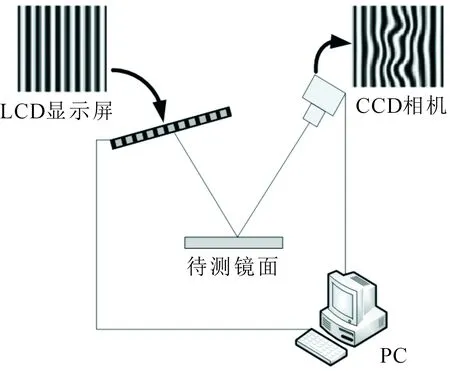
图1 条纹反射检测装置结构示意图Fig.1 Schematic structure of a fringe reflection detection device
计算机控制LCD显示屏显示具有已知参数的结构光条纹,经光学元件表面反射,通过CCD相机拍摄反射面对已知图像的调制。当待测镜面表面不平整时,拍摄到的条纹会产生相应的变形。通过对变形条纹进行相位提取,根据条纹的位相信息确定光线的偏折,利用光线追迹原理,分别向待测镜投影水平和竖直方向的结构光条纹,求得其在水平和竖直方向的梯度分布,重建获得待测物体的表面三维形貌分布。
本文所采用的液晶显示屏分辨率为1 440 pixel×900 pixel,像素间距为0.285 mm;CCD相机分辨率为1 280 pixel×960 pixel,镜头焦距为25 mm,标称像元尺寸4.65 μm×4.65 μm。同时考虑到从CCD获取高质量条纹以减小相位误差,最终选择的一维正弦条纹周期为30个像素,调制度为0.35;相机镜头F数为8。
1.2 面形重建数学模型
由于通过条纹反射法获得的是光学元件面形梯度数据,因而在进行面形重构时,首先需要对Zernike多项式进行求导,获得其梯度函数[19],进而求解Zernike系数。面形重构过程为:
认为被检光学元件表面光滑且连续,其面形可以表示为
w(x,y) =a1Z1(x,y)+a2Z2(x,y)+…+anZn(x,y)
(1)
式中:w(x,y)为面形函数;Zk(x,y)为平面直角坐标系下的泽尼克多项式;ak为泽尼克多项式的系数;n为泽尼克项数。根据式(1)分别对x,y求导可得:
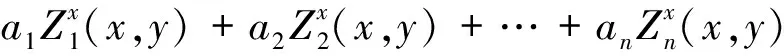
(2)
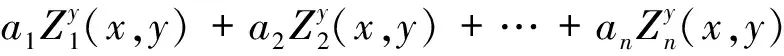
(3)

(4)

a=(ATA)-1(ATS)
(5)
由式(5)确定Zernike多项式系数后,代入式(1)即可重构出待测面的面形。该方法不能给出系数a1,但该项代表平移项,其大小并不影响待测表面的形状,可以不予考虑。
2 仿真结果与分析
本文利用计算机模拟仿真的方法验证所述算法在实际测量实验中的有效性。考虑到双曲面属于二次曲面,可作为一种非球面状态进行研究,从面形的复杂度及特殊性出发,选择连续光滑双曲面作为最终的仿真测量面形。利用 Matlab软件,通过已知参数的设置直接生成仿真面形,然后对面形各点分别求得沿水平和垂直方向的梯度数据,作为算法检验所需的初始数据,进而实现面形重构。
2.1 Zernike多项式项数的选取
Zernike多项式项数选取的不同会对波面精度造成一定的影响。理论上来说,Zernike多项式项数越多,拟合精度越高,越能真实的反映波面。目前,有研究学者发现Zernike多项式拟合波面并非项数越高越好,对于一般非球面检测中遇到的实际波面,采用36项Zernike多项式已经完全可以进行描述[17]。
在项数选定后,采样点的数目会影响拟合精度。采样点过少,会导致拟合后的波面与真实波面存在较大偏差,过多则会导致计算量大和拟合时间较长。有学者对Zernike拟合精度与采样点数目之间的关系进行了探讨,文献[16]通过建立不同的测试函数,采用不完全归纳法研究了采样点数目与Zernike多项式项数的关系,结果表明:当Zernike项数少于30项时,采样点的数目可以取为10倍Zernike多项式的项数;当Zernike项数为30~100项时,采样点的数目可以取为6~10倍Zernike多项式的项数,其中采样点的数目与所选取的项数为反变化关系;当Zernike项数为100~300项时,采样点的数目可取4~ 6倍Zernike多项式的项数。
为研究Zernike多项式项数的选取对本文算法的影响,分别选取前9,16,25,36和49项进行仿真测量分析。假定模拟双曲面方程为
(6)
利用Matlab软件生成如图2所示的模拟双曲面。根据式(6)对高度z分别求取水平、垂直两个方向的梯度,得到如图3所示的梯度分布,作为后续面形重建算法所需的初始数据。
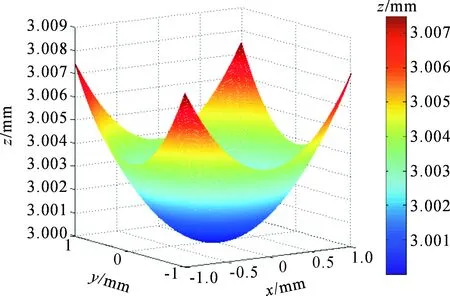
图2 模拟双曲面Fig.2 The simulated hyperboloid
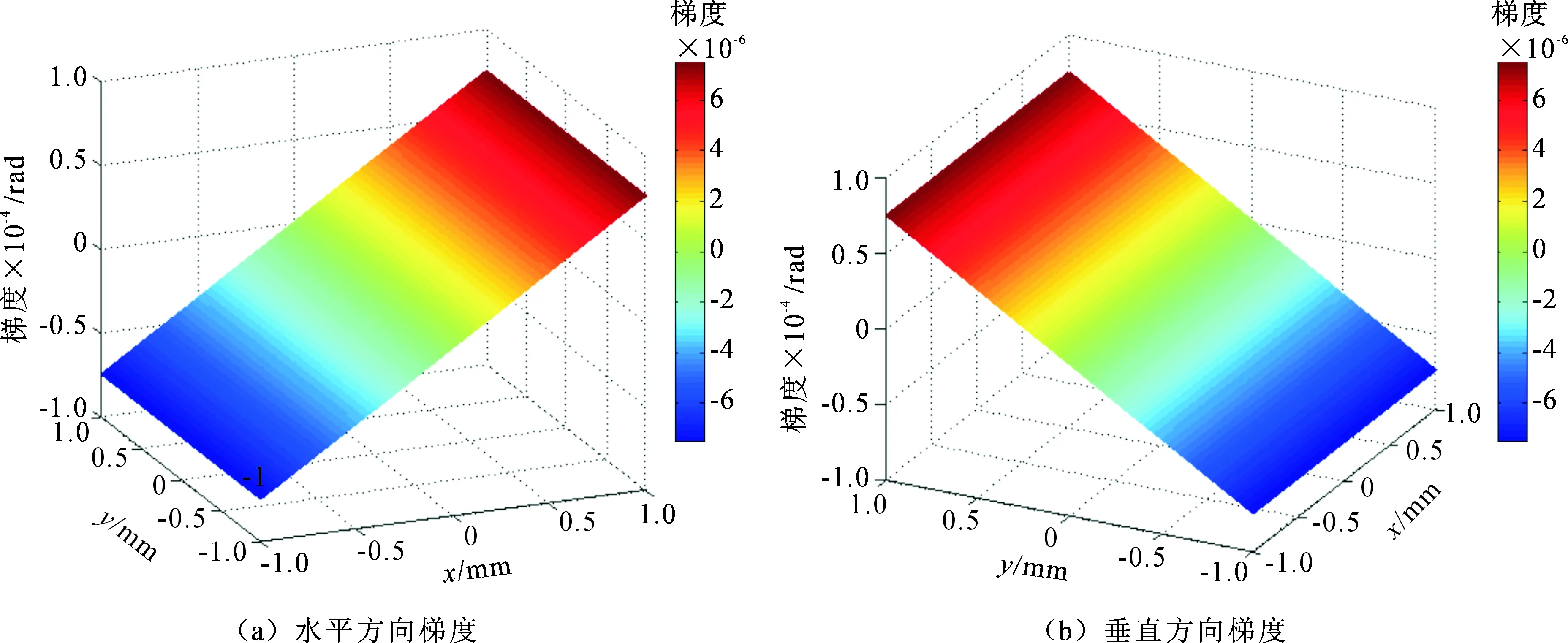
图3 模拟双曲面梯度分布图Fig.3 Gradient distribution of the simulated hyperboloid
采用面形重建算法模型,分别选取Zernike多项式前9,16,25,36和49项进行重建,重建结果见表1。从表1可以看出,对于模拟双曲面,随着Zernike 项数的增加,重建精度逐渐提高,当项数达到25项以上时,面形偏差峰谷值(Peak to Valley,PV)很小(10-15量级)且基本不变,均方根值(Root Mean Square,RMS)在36项达到最小,但在49项出现了增大的趋势。考虑到算法的复杂性,本文最终选择Zernike多项式前36项系数、采样点数为300进行面形重构,认为此时算法的理论精度较高,重建效果图如图4所示。

表1 采用不同Zernike多项式项数的面形重建结果
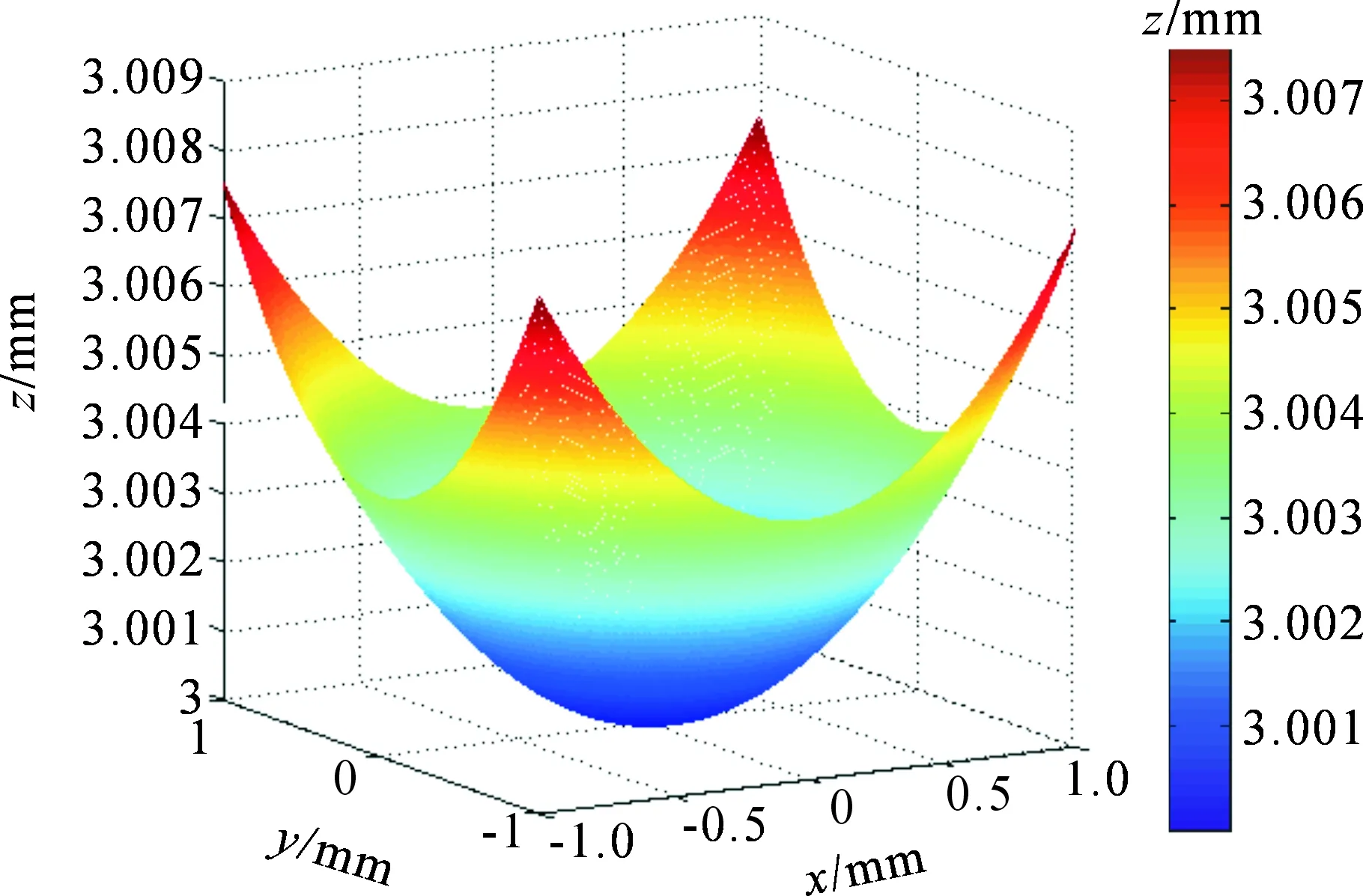
图4 模拟双曲面重建结果Fig.4 Reconstruction results of the simulated hyperboloid
为进一步说明本文算法在测量精度方面的优越性,基于文献[13]的Southwell模型迭代补偿区域波前重构基本思想进行了算法编写,并与Zernike重建算法进行对比分析。考虑到实际过程中算法迭代次数的增多会引起噪声的扩散及处理时间的线性增长,本文进行了3次迭代。图5为面形重建误差图,其中图5(a)为基于迭代补偿的区域波前重构误差分布,图5(b)和图5(c)分别为选择Zernike前9项和Zernike前36项的算法重建误差图。
由仿真结果可知,对于一个初始面形PV=0.007 5 mm,RMS=0.001 1 mm的双曲面,选择迭代补偿区域波前法,拟合面形残差PV=1.675 8e-09 mm,RMS=6.830 4e-11 mm;选择Zernike前36项,拟合面形残差PV=2.664 5e-15 mm,RMS=4.661 6e-16 mm;两种方法的处理时间(矩阵大小均为300×300)分别为2.503 6 s,2.979 6 s。仿真结果表明,本文所提出的算法在几乎不增加处理时间的情况下,一定程度地提高了积分精度,有效验证了该算法的优越性,且在36项以内,Zernike项数越多,拟合精度越高。表2为重建面形的36位Zernike多项式系数。

图5 面形重建误差图Fig.5 Surface reconstruction errors
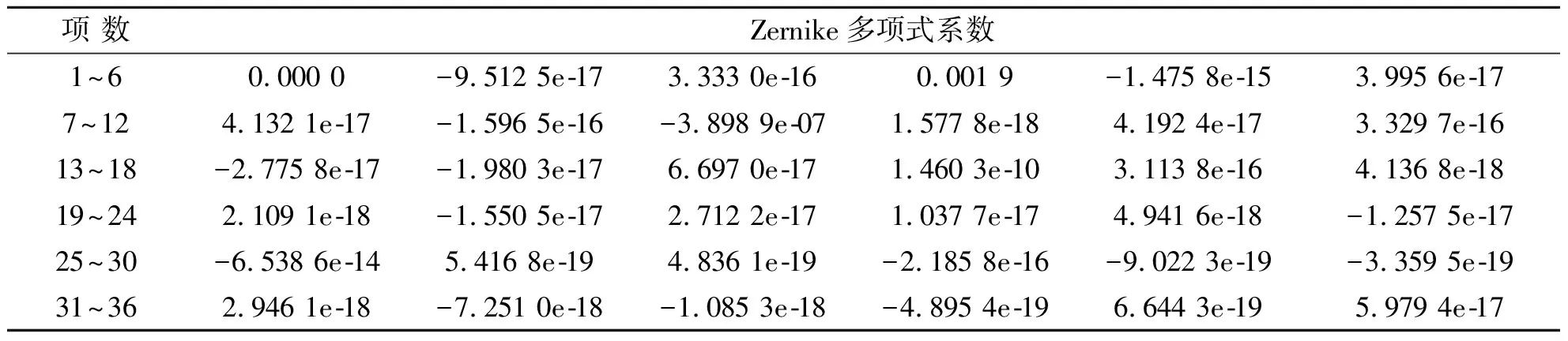
表2 重建面形的36位Zernike多项式系数Tab.2 36 bit Zernike polynomial coefficients for the surface reconstruction
从表2可以看出,本文所提出的面形重构方法是利用Zernike多项式中每一项与光学系统中波像差一一对应的关系,在获得面形重建结果的同时能够准确地给出初级像差系数。该方法不能给出平移系数,但该项并不影响待测表面的形状,因此可以忽略。其次,由于条纹反射法的误差主要来源于系统标定,引入的面形偏差主要是低频面形偏差,该方法还可以进一步去掉泽尼克低阶项后对中高频误差进行分析比较,为复杂的镜面条纹反射测量提供参考。
2.2 噪声等级变化分析
考虑到实际测量过程中不可避免的存在各种噪声干扰,抗噪性能也是检验算法可行性的必要考察手段。在仿真模拟时向水平和竖直两个方向的梯度数据中加入不同等级的噪声,分析算法对噪声的敏感程度。由于添加噪声进行仿真是基于数学统计的方法,单次的运算误差不能说明方法的正确性。本文分别向仿真测量时得到的水平和竖直两个方向的梯度数据加入1%~20%不同大小的噪声,并对每一次添加噪声后的面形偏差进行50次的循环统计。图6为添加5%噪声后的面形偏差分布图。从图6可以看出,经过50次的循环统计,相对运算误差分别为0.8%和1.4%,对算法的影响很小可以忽略。表3为添加不同大小随机噪声的面形重建结果,其中PV和RMS值为50次循环统计计算的平均值。
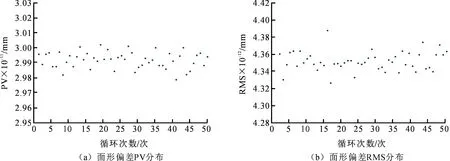
图6 添加5%噪声后的面形偏差分布图Fig.6 The distribution of the surface deviation after the addition of 5% noise

表3 添加不同大小噪声的重建结果Tab.3 Reconstruction results with different sizes of noise
从表3可以看出,随着添加噪声的不断增大,重建后的面形偏差PV和RMS值也不断增大,当噪声≤15%时,PV和RMS值很小,即噪声对算法的影响较小;当噪声达到20%时,PV和RMS值有较明显变化,此时相对面形偏差达到1%和0.4%左右,算法受噪声影响增大。因此,该算法在噪声大小为15%以内有很好的适用性。
3 结 论
本文提出了一种基于Zernike正交多项式的面形重建方法,通过理论推导,建立了面形重建数学模型,得出结论为
1) 分析了Zernike多项式项数与采样点数的关系,分别选取前9,16,25,36,49项进行仿真测量,研究Zernike项数对本文算法的影响。结果表明:在36项以内,Zernike 项数越多,拟合精度越高;当项数达到49项时,面形偏差PV值基本不变,但RMS值出现了增大的趋势。
2) 以双曲面为例对基于迭代补偿的区域波前重构法(迭代3次)与Zernike重建算法进行分析对比。本文所提出的算法在几乎不增加处理时间的情况下,一定程度地提高了积分精度,有效验证了该算法的优越性,并给出了重建面形的36项Zernike多项式系数,其中离焦项较大,但该项是由系统摆放误差造成,后续可将其去除并对面形高频误差进行对比分析。
3) 通过对梯度数据添加1%~20%不同大小的噪声,并对每一次添加噪声后的面形偏差进行50 次的循环统计,以进行算法的抗噪性能检验。当噪声不大于15%时,算法有很好的适用性。
