基于复合BP神经网络的天然气工况监测系统研究
2019-04-02沈国良苏祥伟
沈国良,苏祥伟,谭 汉,邵 迪
(1.浙江浙能天然气运行有限公司,杭州 310012;2.浙江浙能技术研究院有限公司,杭州 311121)
0 引言
浙江省天然气管网为省级干线网络,沿线设置有发电厂输配站,直接对接发电厂燃气机组,通过SCADA(数据采集与监控)系统的控制调节来满足机组运行时对压力和流量的要求,而采用智能系统代替人对机组运行时的复杂工况进行实时监控是站场无人化的关键核心。
天然气输配调节的本质就是在调节前后存在差压的前提下,通过改变调节阀的阀位来改变输配气的工况流量,同时当输配环节发生异常,如阀门误动、计量故障等时,最直接的表征就是实测流量发生变化,所以对天然气输配进行工况监测,其直接有效的方式就是建立压差、阀位和流量之间的系统模型,通过对流量的跟踪分析来实现工况监测的功能。
1 研究背景
天然气站场无人化建设规划中,以站场集中监控、统一管理的方式进行调度和运行管理,而传统的站场值守模式完全依赖于运行人员的经验来对整个输气工艺状况进行分析评价,当集中监控后,由于监控点的成倍增长,监管频率和难度也相应增加,且长时间的监盘极易导致习惯性疲劳,存在风险隐患。在供天然气发电机组的发电厂站,由于机组负荷大、工况变化复杂、反应时间短等特点,即使传统的站对站监控模式,也会因调节故障、阀门异动等原因导致机组甩负荷甚至跳机。所以,在实现发电厂站的集中监控前,首先需要解决的问题是如何进行供气状态的智能分析,并提前预警,再以此为基础,通过系统或人为干预来保证供气的稳定性。
但是目前针对天然气输配控制的建模和分析主要集中在管网的仿真调度方面[1-5],而对于以站场或用户为单位的具体调节系统,其建模主要采用多元函数拟合的方式[6-8]来实现,但是在气体的计量过程中,需要充分考虑组分、管道、流态、压缩因子、流出系数等多个不确定因素,所以通过多元函数建立准确的数学模型非常困难。
对于复杂及非线性系统,神经网络的应用非常广泛,但在天然气的输配领域,神经网络主要用于气量预测和供气的可靠度计算[9-10],极少用于流调控制[11],所以对于单个流调系统来讲,关键在于一定前提下,工况体积流量、调节阀阀位、调节的前后压差这3个参量是否存在对应关系[12],通过天然气管输调节控制仿真模型[13],同一站场中由于工艺条件不变,且对于工况体积的计量只取决于管道压差和管道工艺,从而排除了组分、补偿系数、压缩因子等相关系数的影响,所以对于单条支路,完全可以通过数学函数建立模型。但在实际应用场景中,特别是对于发电厂用户,要保证系统的稳定可靠运行往往需要主、备支路同时使用,在该种工况下,由于流态、调节扰动等相关因素的影响,不能简单地通过单一支路模型叠加方式进行计算,所以需要借助神经网络强大的非线性拟合能力来建立系统模型。
2 模型建立
通过神经网络进行系统建模,关键是用于训练的样本具有代表性和覆盖性,以浙江省天然气管网所属某发电厂站(见图1)为研究对象,从省网调控中心的数据库中检索了2012年1月—2018年8月的样本数据,并从中挖掘出具有典型性的5万组样本进行建模,将样本以三参量综合排序后,按照奇偶序号划分成相近的各2.5万组样本数据,分别用于训练和验证。

图1 某发电厂站流调工艺
2.1 数据的预处理
样本数据的覆盖面较广,分布差异较大,所以需要将数据进行归一化处理。归一化即标准化,是将不同数量级的数据转变成同一数量级的方法,以此来减少样本数量级对拟合准确性的影响,同时,考虑神经网络输出层激活函数的值域限制,所以需要将网络训练的目标数据映射到所选用的激活函数的值域。
采用了最大-最小标准法,对于每一个变量X,通过式(1)进行变换,使得变换后样本数据X′的范围都在[-1,1]区间:

式中:min为X的最小值;max为X的最大值;X′为归一化后的X。
式(1)将数据归一化后,相应地在网络的输出层,激活函数采用双极S形函数,见图2。

式中:x为前层各神经元输入当前神经元的加权和;f(x)为神经元激活后的输出;α为激活函数的调整系数,协同学习率对网络的性能进行优化。
2.2 神经网络结构
在网络构建时,首先采用LM-BP[14]网络,其结构见图3。

图2 双极S形函数

图3 LM-BP神经网络结构
其中,输入向量3个,分别为PV1(一支路调节阀阀位)、PV2(二支路调节阀阀位)、 DP(压差);输出向量1个,为QW(工况流量);隐含包含250个神经元,人工神经元模型如图4所示;每一个输入,通过式(1)变换后进行输入,经过式(3)加权求和后,通过式(2)输出:

式中:i为网络层数;n为每层的神经元数量;ω为神经元的连接权;θ为偏置,并作为ωi0计算;neti为输入当前神经元的加权和,即式(2)中的x,y为计算值,同时为下一层神经元的输入x。
模型的损失函数采用均方差MSE,其中e为误差,N为样本数量,同时计算均方根差RMSE进行匹配度的评价:


图4 人工神经元模型
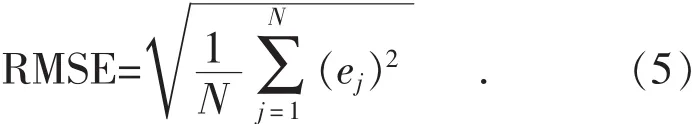
采用Levenberg-Marquardt法进行训练和验证后得到的误差分布分别如图5、图6所示。

图5 LM-BP神经网络的训练误差
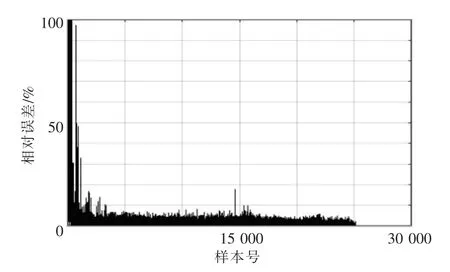
图6 LM-BP神经网络的验证误差
观察图5和图6,在500 m3/h以上区域,网络的训练效果较好,误差基本控制在5%左右,验证时少量数据误差超过10%,可考虑系统误差;但在500 m3/h以下的小流量区,网络的拟合误差较大,主要原因为:一是计量准确度的问题,研究站场所用的超声波流量计标称量程为5 000 m3/h,有效计量的最低范围为10%,即500 m3/h,该区间的计量不确定度较大;二是调节阀的调节特性问题,小流量区域的调节阀位基本在10%~15%(见表1),处在阀门的非线性区域,流态也不稳定。所以综合来说,小流量区域的函数关系不同于大流量区,需要额外处理。
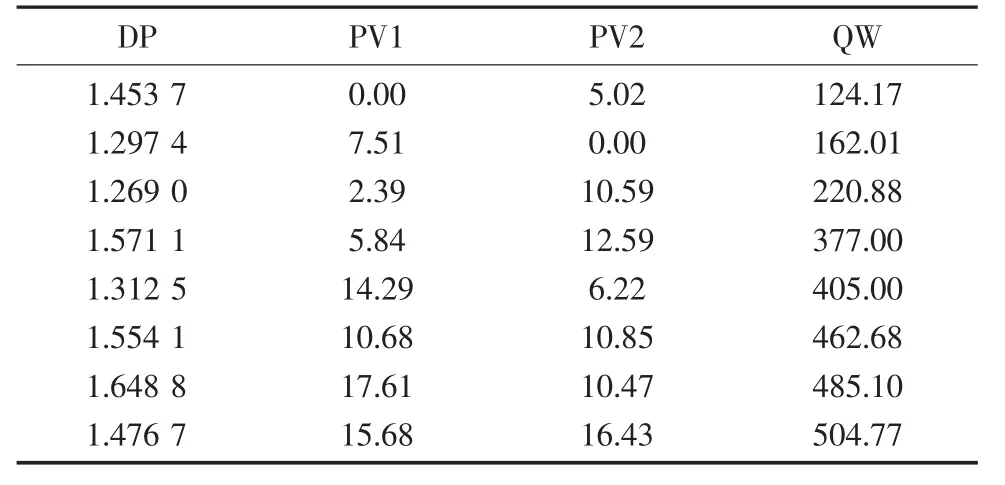
表1 小流量时的各参数
在小流量区单独构建CGF-BP[14]网络,如图7所示,通过共轭梯度法进行训练,通过样本验证后,采用绝对误差进行评价,如图8所示。

图7 CGF-BP神经网络结构
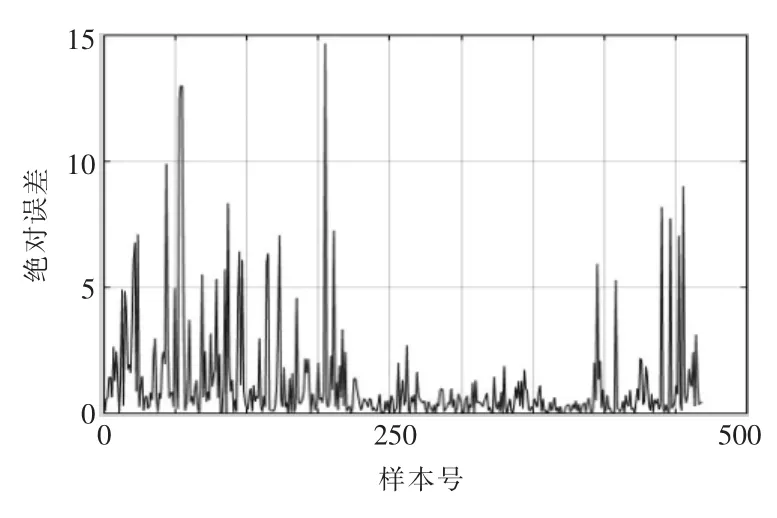
图8 CGF-BP神经网络验证的绝对误差
最后将2个神经网络结合,首先通过LMBP进行拟合计算,当计算结果小于500时,通过CGF-BP进行修正,通过复合神经网络[16]来优化拟合过程,形成最终的模型,其计算流程如图9所示。
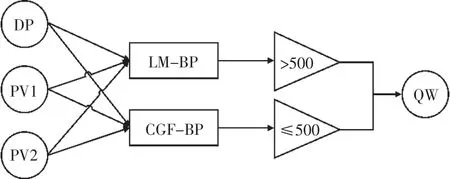
图9 复合网络的计算流程
对模型进行样本验证的结果见图10和图11,可以看出,在验证结果上,模型基本实现了拟合的误差要求。
3 实际应用
模型训练完成后,考虑到网络的计算效率,设置2 min 1次的采样及分析频率,通过对该发电厂站4个起机-运行-停机的完整工况比对,进行实际测试。模型共分析了2 800多组工况数据,比对结果见图12;同时为检查模型对异常工况的监测效果,对流量计的补偿压变进行屏蔽处理以模拟计量系统故障,由于差压和调节阀的阀位正常,模型的计算值会延续正常工况,比对结果如图13所示。

图10 复合网络的验证拟合

图11 复合网络的计算值比对

图12 复合网络的实际比对效果

图13 复合网络的模拟故障监测效果
从图12的拟合情况分析,模型基本实现了对实际工况的高度还原,但是对于小流量的拟合方面相对误差较大,考虑系统不确定度和样本量级,认为结果处于可接受范围;在总体的拟合误差方面,除不可避免的系统检测误差,系统误差控制在5%左右,与训练和验证的误差基本保持一致,这也说明训练样本数据的覆盖面较好,模型的辨识度较完善。
图13中在样本号100~160区间计算值和实测值之间有一个明显AE(绝对误差),根据表2数据,其RE(相对误差)达到20%~30%,通过这个差值,并过滤掉系统误差的干扰,即实现了对异常工况的监测功能。

表2 模拟计量故障时的各参数
4 结语
在天然气调节系统的运行过程中,调节工况随着运行时间不断累积大量的数据,目前这类数据在进行备份存档后极少进行开发利用。因此,对系统的数据进行充分挖掘、分析处理后,选取典型数据进行系统建模,在匹配性、覆盖程度、准确性等方面均取得了良好的效果。
由于缺少神经网络在天然气输气调节控制及工况监测中的应用案例借鉴,所以在系统的开发过程中,通过多次测试,选择了LM和共轭梯度等改进型训练法,但是BP网络在梯度下降法的训练过程中还是难免陷入局部最优解的问题。同时,为避免拟合误差过大,采用了分段拟合的方式来进行函数逼近,整个系统结构相对比较复杂,计算效率偏慢,而且在计算值转换过程中容易导致损失函数的失控,所以在后期的研究过程中,可以采用更有效的复合神经网络及深度学习的方式来完善功能,提高工作效率。
