基于优化型SVM的高压断路器故障诊断方法研究

2019-04-02周建平万书亭杨晓红

浙江电力 2019年3期

周建平，李聪，万书亭，杨晓红

（1．国网浙江省电力有限公司检修分公司，杭州 311232；2．华北电力大学机械工程系，河北保定 071003）

0 引言

高压断路器在输、配电网中起着重要的保护和控制作用，因其工作环境恶劣导致较高的故障率，因此开展断路器故障诊断十分必要[1-2]。分合闸线圈电流信号可以反映断路器铁心卡涩、传动机构卡滞、控制回路电压等工作情况，同时在采集时具有非侵入性，不会影响断路器的正常运行[3-5]。本文以分合闸线圈电路信号为研究对象，对断路器运行状态进行评估。

在以往学者对电流信号的研究中，赵钰[6]等人在模糊理论的基础上有效提取了分合闸线圈电流时间和电流值，为后续断路器故障状态分析提供了依据。杨为[7]等人提出了一种基于样条插值和多尺度线性拟合的方法，对断路器分合闸线圈电流进行特征提取，可以准确区分断路器的不同状态。周凯峰[8]等人以电流时间和电流值为特征，并计算特征量的均值及方差，使用95%的置信区间作为阈值，构建了故障诊断系统，对故障电流检测结果较好。但上述研究只考虑了时域中的局部特征，本文则在局部特征的基础上，加入了均值、标准差、峭度和能量参数4个特征，并将其作为电流信号的全局特征；再将局部特征和全局特征作为电流信号的特征向量，对断路器的部分故障状态进行识别。

对断路器模拟故障信号进行分析时，考虑到多种特征参数的相关性会对分析造成困难，且特征参数较多会造成分类训练时间长，影响识别效果，所以需要一种有效的数据处理方法，以减少数据计算量并快速提取信号有效信息。PCA（主分量分析）法是一种通过坐标变换把高维空间信息转换到低维空间的方法，该方法将相关变量变为少数不相关的主分量来表征原来的信息，简化分类过程。李慧[9]等人应用PCA法对棉花和杂草特征进行空间降维，有效减少了识别方法的训练时间，并提高了分类正确率。刘永斌[10]等人利用PCA法消除了内燃机多路振动信号中的冗余特征，实现了多诊断参数融合，较好地表征了断路器不同状态的特征。张勇[11]等人利用PCA法对信号进行降维并消去相关性，获得了主要的特征数据。在常见的模式识别中，大部分方法都需要足够多的训练样本来保证分类的正确率，而断路器模拟故障样本数量有限，所以需要选取一种适合小样本分类的模式识别方法。SVM（支持向量机）在有限的样本信息的基础上，将样本点误差最小化，缩小了模型预测误差的上界[12]，是一种适合小样本分类的模式识别方法。茆美琴[13]等人采用SVM法对光伏电站短期出力进行预测，通过选取不同的核函数和参数得到了较好的预测精度。孙曙光[14]等人应用基于遗传算法优化权值系数的多核学习SVM对断路器分合闸线圈电流进行故障诊断，效果良好。

本文以电流时间、电流值、电流均值、标准差、峭度和能量为特征参数，采用PCA-SVM方法对断路器运行状态进行评估。针对正常状态、合闸弹簧疲劳、传动机构松动和控制回路电压低4种故障进行模拟试验，结果表明该方法能够快速提取信号特征的有效信息并对断路器运行状态进行有效识别。

1 电流信号机理分析

在高压断路器的运行过程中，通过监测分合闸线圈电流的变化，可以间接了解铁心的状态变化。通过分析线圈电流的特征，可以充分了解铁心的工作情况，以及弹簧操作机构的部分运行状态，为高压断路器的故障防范和检修计划提供一个辅助判断。图1所示即为典型的分合闸线圈电流信号曲线，该曲线分为4个阶段。

图1 典型分合闸线圈电流曲线

0-T1：0时刻，线圈开始通电，电流呈指数上升，在此过程中，电流产生的电磁力逐渐增强；到T1时刻电流达到第一个波峰，此时电流产生的电磁力大于铁心所受的外界阻力，铁心开始运动。该阶段可以反映线圈电压、回路电阻以及铁心是否卡滞等情况。

T1-T2：T1以后，铁心开始运动，此时线圈电流减小，到T2时刻，电流达到最小值。在此过程中铁心的速度急剧降低，到T2时刻，铁心撞击锁扣/脱扣装置，然后停止运动。此阶段可以反映铁心运动卡涩情况和脱口失灵等故障。

T2-T3：T2时刻铁心停止运动后，传动机构的锁扣被打开，此阶段电流持续上升，动触头开始动作，分闸弹簧开始分闸；到T3时刻，电流达到峰值。该阶段可以反映传动机构的运动状态。

T3-T4：T3时刻动静触头完全分离，辅助开关断开，切断线圈电源，触头间产生电弧，电弧电压在短时间内急剧增加，这直接导致电流急剧减小；T4时刻，电流减小为0。该阶段的电流曲线可以反映辅助开关是否存在故障。

2 电流信号特征分析

在对断路器分合闸线圈电流进行研究的文献中，几乎都是以电流时间和电流值为特征向量来进行分析，但在实际工作过程中，制造工艺、运行工况等因素会导致同一型号的不同断路器特征量的差别，同一断路器在不同时刻的特征量也会有一定程度的差异，所以仅仅以电流时间和电流值大小为特征对断路器工作状态进行判断具有一定的局限性。本文在电流时间和电流值的基础上，加入了均值μ、标准差σ、峭度K和能量参数W，共采用11个特征参数来反映断路器工作状态。

均值μ可以反映信号的稳定程度：

式中：xi为随机变量的取值。

标准差σ能够描述数据的离散程度，在信号分析中，可以用来表征信号的能量：

峭度K为一个四阶统计量，反映信号分布特性，是随机变量非高斯性的最简度量：

能量W代表合闸电流做功大小，W的大小取决于电压U、电流I和时间T：

式中：U为控制回路电压；I为合闸线圈电流值；T为时间。

3 PCA原理

PCA[15-16]是多元统计分析中的一种数据分析方法，通过将高维向量映射到低维空间以达到降低空间维数的目的，在降维过程中，保留了信号的主要信息，通过低维向量和特征向量矩阵可以基本重构出所对应的原始高维向量。

设断路器振动信号有k个训练样本，每个样本有n个特征值，其列向量为 xk=（x1k，x2k，…，xnk）T，该样本集的平均向量为，协方差矩阵求出协方差矩阵的全部特征值λi和特征向量vi，特征向量构成一个m维正交空间。按从大到小的顺序，将特征值λi排列为 λ1＞λ2＞…＞λd＞λd+1＞…，由于样本信息集中在特征值较大的特征向量中，舍弃一些特征值小的特征向量不会对信息造成影响，所以选取大于λd的特征向量构成主分量。样本xi投影到特征向量vi，得到该方向对应的主分量为。设正交空间中d个主分量为y1，y2，…，yd，累计方差贡献率为

累计方差贡献率可以决定主分量的选取个数，本文中累积方差贡献率取H（d）＞95%，即只选取前d个主分量来表征原始信息，前d个主分量包含原始信号95%以上的有效信息，从而达到降维的目的。

4 试验分析

4.1 算法流程

基于PCA和SVM的故障诊断算法流程如图2所示。

图2 算法流程

（1）特征提取。提取合闸线圈电流信号的时间参数、电流参数、均值、标准差、峭度和能量共11个特征参数。

（2）PCA降维。将所有特征标准化，进行PCA降维，获得有效的特征向量。

（3）SVM分类。将得到的有效特征向量输入SVM进行训练和预测，获得工作状态分类结果。

4.2 试验模型

试验对象为一台户外工作的35 kV SF6高压断路器，通过预先设定故障方式来模拟断路器可能的4种运行状态：正常状态、合闸弹簧疲劳、传动机构松动和控制回路电压低。其中，合闸弹簧疲劳是通过松动合闸弹簧固定螺栓实现的，传动机构松动是通过调节机构连杆长度实现的。为了保证模拟故障的准确性，遵循单一变量原则，每次保证断路器仅有一个故障。

4.3 特征提取

受噪声和测量环境的影响，采集到的分合闸线圈电流信号往往伴有小的尖刺或者小的凹陷，因此采用3次样条插值方法对原始信号进行光滑处理。由于电流曲线两点间的间隔足够小，可以用相邻两点间的斜率近似代替该点的导数，从而用近似求导法获得合闸线圈电流信号的时间和电流值特征。

对于大部分信号，会获得3组极值，但是曲线中仍不免存在一些小尖峰和波谷，有时会出现多于3个极值点的情况。因此要对检测到的极值点进行分组处理，分组数量根据分合闸电流具体试验数据确定。根据合闸电流曲线波形可知，波峰波谷的出现顺序是先波峰再波谷最后又是波峰，故将电流信号分为3组，分别求取3组极值数据中的y值最大值、最小值和最大值即可。

利用公式（1）—（4）可获得电流信号的均值μ、标准差σ、峭度K和能量W特征，共提取11个参数。选取断路器正常状态、合闸弹簧疲劳、传动机构松动和控制回路电压低4种状态的合闸电流信号，每种状态采集30组数据进行特征参数提取，构成一个120×11的特征矩阵，部分数据如表1所示。

由于每个特征参数所代表的物理意义不同，参数的尺度也大小不一，故采用均值-方差标准化方法对参数进行标准化处理。图3以样本点数为横坐标，归一化的值为纵坐标，反映了4种状态下合闸电流信号的11个特征参数的变化趋势。

图3 合闸电流信号特征参数变化趋势

从图3可以看出，每个特征参数对断路器运行状态反映趋势和规律性不同，有些对故障状态不敏感的参量增加了计算的负担，应该滤除，所以采用PCA法对特征参数矩阵进行降维处理，以提取特征参数的有效信息。

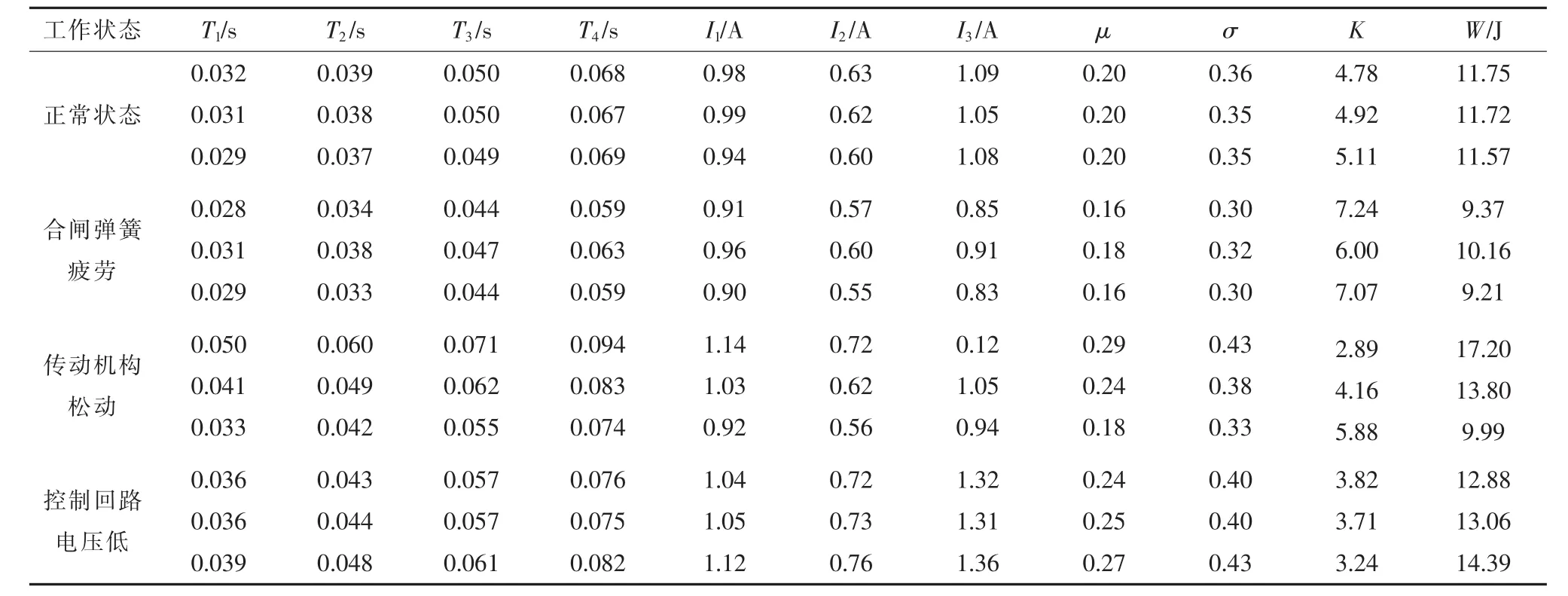
表1 合闸线圈电力特征参数

4.4 特征降维

采用PCA法对信号进行如下处理：

（1）用均值-方差法对所有信号进行标准化，消除不同量纲之间的差异。

（2）求取特征参数矩阵的协方差矩阵。

（3）求取协方差矩阵的特征值和特征向量，按从大到小的顺序对特征值进行排列，得到对应的特征向量。

（4）求取主分量和主分量贡献率。主分量为按照顺序排列后的特征向量，主分量贡献率为每个主分量所包含有效信息的比重，主分量贡献率=特征值/∑特征值。

表2为11个主分量贡献率和主分量累积贡献率，将其绘制成曲线（如图4所示），可以更直观地表示单个主分量贡献率和主分量累积贡献率的规律和特征。根据第3节对于PCA原理的介绍，PCA本质上是将方差最大的方向作为主要特征，方差越大，说明在该方向上变化越明显，在向量重构过程中贡献率越大，所以将重构分量按照方差从大到小的顺序排列，选取累计贡献率不小于95%的前N个主分量。由图4可知，前3个主分量的累计贡献率达到了97.84%，所以选取前3个主分量作为新的特征向量来表征原信号。部分主分量特征如表3所示。

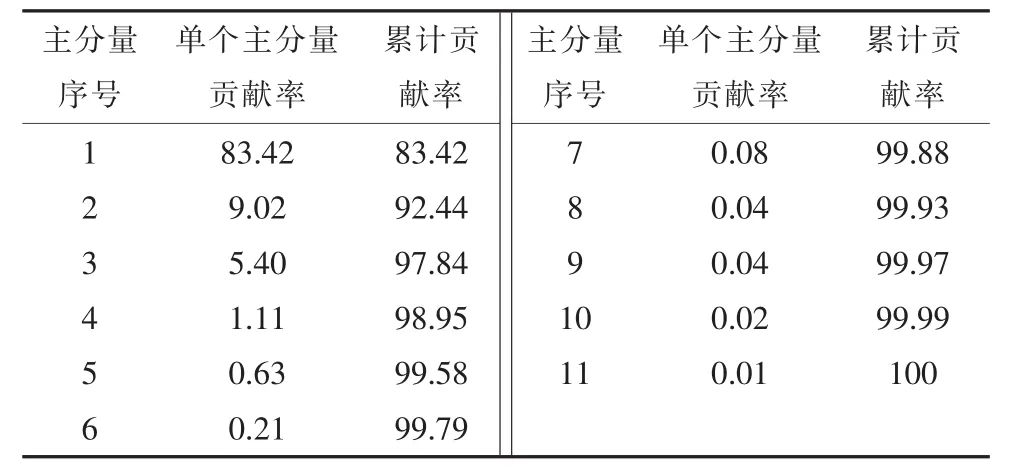
表2 单个主分量贡献率和累加贡献率%

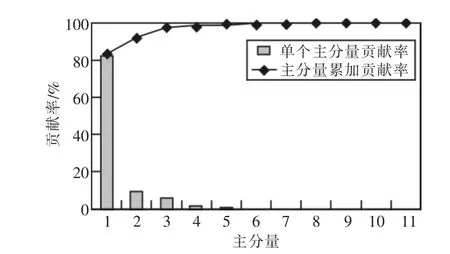
图4 单个主分量贡献率与累加贡献率

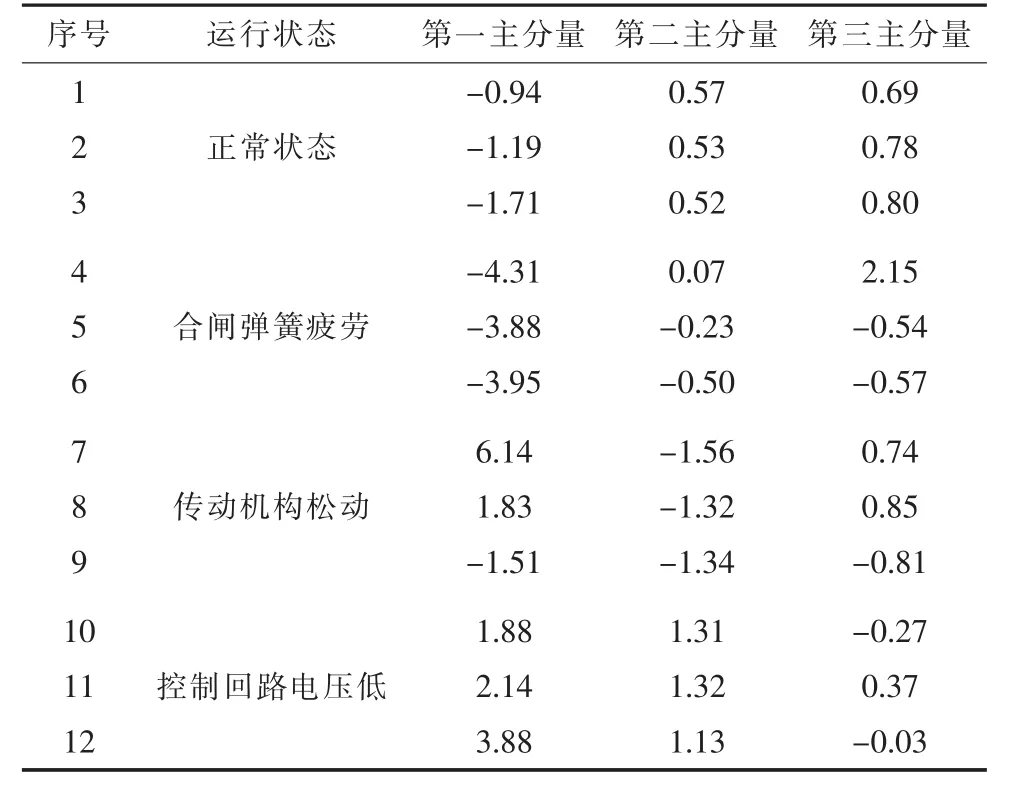
表3 PCA降维后的部分特征参数

4.5 故障分类

取断路器正常状态、合闸弹簧疲劳、传动机构松动和控制回路电压低4种状态的合闸线圈电流信号各30组，经PCA降维，得到120×6的特征矩阵，每种状态对应30×6的特征矩阵。选取前24组数据用于训练，后6组数据用于测试，选用径向基核函数对样本进行支持向量分类训练，构造4个“一对三”的SVM，得到分类结果如图5所示，正确率为91.67%，效果良好。

图5 SVM分类结果

本文分别对原局部特征（电流时间、电流值）、PCA降维后的局部特征、原综合特征（电流时间、电流值、均值、标准差、峭度、能量）和PCA降维后的综合特征用SVM进行分类识别，得到结果如表4所示。

表4中，通过1与2对比，3与4对比可知：PCA降维后的特征向量在分类正确率和程序运行时间上都具有明显的优势，说明PCA在保证信号有效信息的基础上可以剔除冗余成分，提高计算效率；在传统电流特征向量基础上加入全局特征，组成综合特征，对于断路器状态识别效果更好，有效提高了分类正确率。

表4 不同特征分类效果对比

在分类识别的过程中，分类器的选择对分类效果影响巨大，较为经典的方法是BP神经网络。采用BP神经网络对特征向量进行分类识别，训练73次，隐含层数为2，输出层1个。将综合特征用SVM和BP神经网络的分类效果对比如表5所示，结果显示，SVM在小样本分类问题上的综合分类性能优于BP神经网络，对于断路器故障状态识别具有较强的实用性。