基于输电线路电磁场分布的无人机测距适应性研究

曹浩楠，王 彬，邹国平，钟素鹏，董建洋

（1．国网浙江省电力有限公司检修分公司，杭州 311232；2．浙江大学电气工程学院，杭州 310027；3.杭州艾参崴电力科技有限公司，杭州 310019）

0 引言

近年来，随着我国经济的持续快速发展，中国电网的规模和输送能力日益壮大。以浙江为例，2010—2017年国网浙江省电力有限公司110～1 000 kV架空输电线路总长从28 000多km增长到50 000多km，整体增长超过70%。

架空线路运维工作日益繁重，运检部门迫切需要更自动化、现代化、高效率的巡线技术和手段。通过多年的技术研发和实践，无人机巡检技术已经发展成一种高效、低成本、低风险的空中巡检技术，是提升输电线路运行可靠性的重要手段之一。与传统人工巡检相比，无人机输电线路巡检不受地形环境限制、视角宽广、精度高、安全性好，经过数年推广应用，无人机巡检已在电力公司得到了广泛应用[1-2]。但从现场应用情况来看，无人机巡线过程中缺少对输电线路的精确测距技术、预警技术与自动避障技术。

目前无人机的可用测距技术包括GPS定位、激光测距、超声波测距、可见光测距等技术[3-6]。GPS定位是生活和生产中常用的距离判断方法，基于GPS的无人机测距技术一般利用地理坐标系的转换和GPS信息计算两点间距离，并基于GPS信息实现无人机云台角度的自动调节，从而达到巡检过程中各个相机对巡检线路中杆塔的跟踪拍摄[3]。但民用级GPS本身存在精度误差，一般系统定位偏差在2.5 m左右，但在复杂山区地形中GPS信号较弱、容易受干扰，其定位误差较大。激光测距是精度比较高的测量方式，常见的激光测距传感器有效测量距离在200 m内，最高精度达毫米级。文献[4]利用无人机-地面激光测距技术和DMC-PID串级控制算法，实现了无人机根据地形自主匹配飞行。但由于高压输电线路导线为多分裂结构，其激光反射面并不连续，且当无人机在线路侧面巡视时，多相导线叠加在同一背景下，激光测距难以分辨具体导线。超声波测距传感器具备声波的扇形发射特性，可利用无人机搭载超声波测距传感器的方式实现输电线路与地面树木之间净空距离的测量[5]，但由于超声波传感器的测距范围有限，一般不超过10 m，无法满足无人机和输电线路的安全距离要求。文献[6]提出了一种基于成像模型的单目视觉的测量方法，首先通过图像处理技术识别出输电线路图像中的输电线杆塔,建立了输电线路的成像模型，据此模型推导计算出了无人机与输电线路竖直平面的安全距离。该方法具有较低的运算复杂度和较高的精度，但该方法需要提前输入杆塔的高度，这一参数在现场巡检中难以获得。

由于现有的测距技术在应用中都有一定的难度，因此在目前的无人机巡检中，大多还是现场操控人员通过肉眼判断与输电线路的距离，这对工作人员的要求极高，同时存在一定安全隐患。针对此问题，本文提出了一种考虑输电线路电磁场分布特性的测距方法。利用有限元算法建立了特高压输电线路的仿真计算模型，分析了特高压输电线路周边的电场、磁场、电场梯度、磁场梯度等电磁分量的分布特性，提出了选用电场有效值结合高度来确定无人机与输电线路真实距离的方法。

1 输电线路电磁场方程

输电线路正常运行时，高压交流输电线路对环境的影响主要包括工频电场、工频磁场、电晕放电造成的无线电干扰和可听噪声等。由于架空输电线路产生的工频电磁场主要存在于线路周围的空间，且工频电磁场为场点到导线的距离远小于相应电磁波的波长，为准静态场。因此可应用静态电磁场的分析方法进行相应的分析与计算。可以得到准静态场所满足的麦克斯韦方程[7：

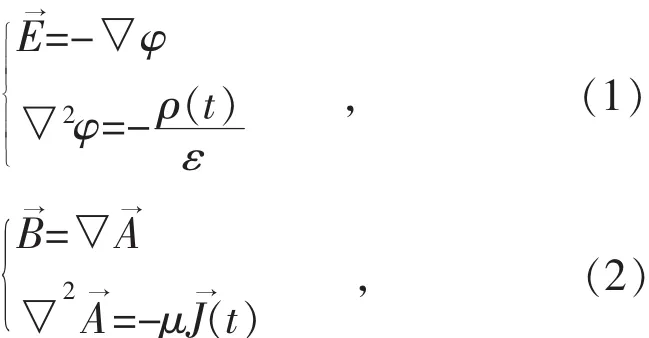
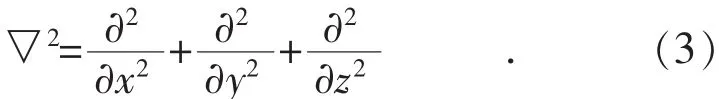
在电磁场微分方程的求解中，只有通过边界条件和初始条件的限制，方程才能有定解，因此需要设置边值和初值。输电线路周边电磁场分布问题构成第一类边界条件，如式（4）所示条件：

式中：rb为相应边界条件的位矢；φ（r）为给定场域边界S上的点位置，它与泛定方程构成第一类边值问题。

2 有限元算法和流程

有限元算法是以变分原理为基础，首先将所求的边值问题转化成泛函求极值问题；然后进行剖分插值，将变分问题离散化普通多元函数求极值问题，最后产生一组多元的代数方程组，求解即得待求边值问题的数值解。静电场的边值问题等价的变分问题如式（5）所示[8]。

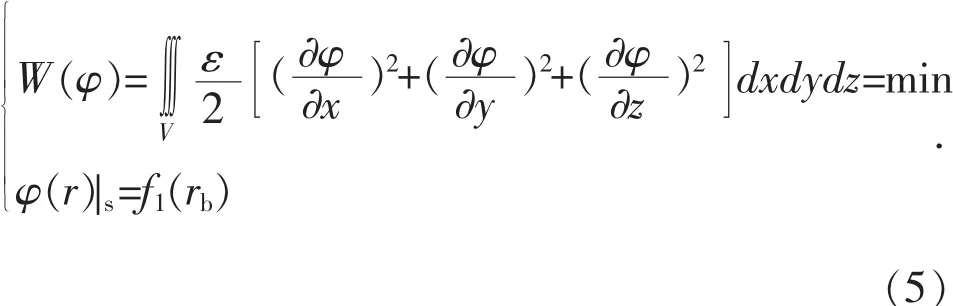
在实际计算中，将场域剖分为有限个单元，每个离散化的单元能量求和，然后求总能量的极小值条件，最后导出线性方程即有限元方程。求解此方程组就可得到电场的近似分布。

Ansoft软件是由John Swanskon教授基于有限元理论首先开发的软件，经过多年完善，Ansoft软件将电磁、热、流体等融为一体，现在已经应用于机械加工制造、电子电气、交通、土木、教学科研等众多领域[9-10]，是应用最广泛的有限元软件。其主要计算流程如图1所示。本文的数值计算工作基于Ansoft完成。

图1 Ansoft有限元分析流程

3 特高压输电线路电磁场分布规律

3.1 杆塔结构

1 000 kV皖电东送特高压南线起于淮南站，经芜湖、安吉，止于练塘站，线路杆塔为钢管塔，具有多种型号和尺寸。图2是应用最多的SZ322塔形结构图，考虑了多类型杆塔结构参数和相缘子串长度与弧垂情况下，仿真计算参数见表1。

3.2 仿真模型

仿真计算采用Ansys的2D Extractor软件，依次计算了输电线路周边的电场、磁场的分布情况。计算中假设输电线沿z方向无限长，故场计算采用沿导线方向的二维场，计算时双回导线相序为同相序，输电线路线电压取1 000 kV，电流取100 A。计算边界为高300 m，宽500 m。

3.3 电场分布

从图3—图5中可以看出，其等电场值线为环绕输电线的封闭曲线。远离输电线时，等电场值线趋向于半圆形；而接近输电线时，等电场值线为不规则形状。因此无法单纯从检测电场值得到观察点离输电线的距离。

3.4 磁场分布

表1 特高压线路典型线路结构

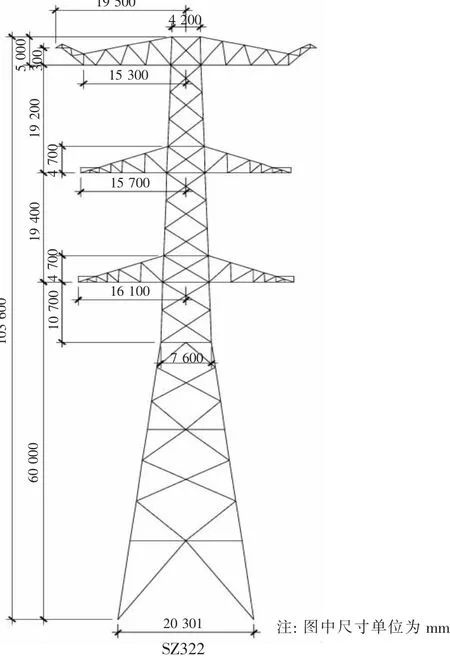
图2 特高压线路典型杆塔结构

磁场分布如图6—图8所示。与电场分布类似，远离输电线时，等磁场值线趋向于半圆形；而接近输电线时，等磁场值线为不规则形状。因此无法单纯从检测磁场值得到观察点离输电线的距离。

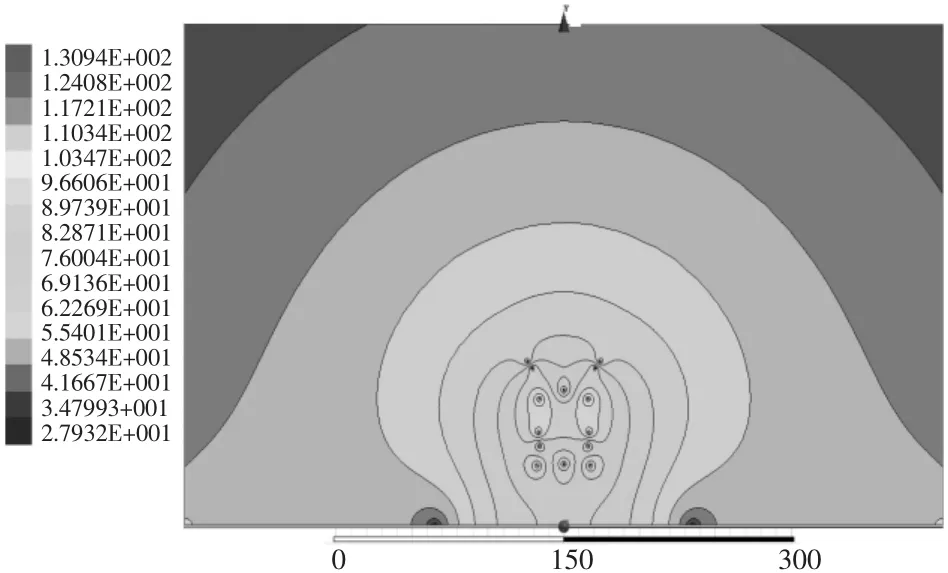
图3 电场有效值

图4 电场水平分量

图5 电场垂直分量

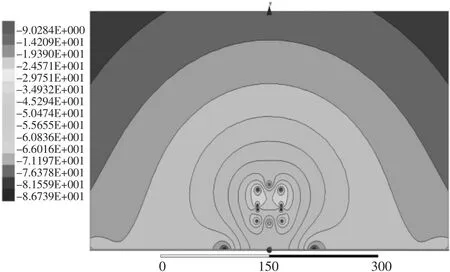
图6 磁场有效值

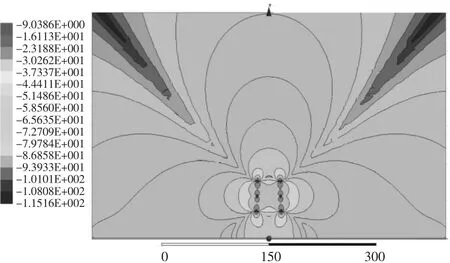
图7 磁场水平分量

图8 磁场水平分量

3.5 电场梯度

文献[11]介绍了以电场梯度作为判断距离远近的方法，但要求无人机到达某一固定高度后只能水平移动，适应性较差。因此本节计算分析了XY平面中电位梯度的变化，电场梯度分布如图图9、图10所示。为了便于分析，使用MATLAB对数据进行了处理。设梯度值为a，取其对数值，如果 a>0，则为 20loga；如果 a<0，则为-20log（-a）；如果a=0，则为0。观察图9和图10发现在XY坐标系内电场梯度没有明显的单调性，不适合作为测距的特征量。

图9 电场水平方向梯度

图10 电场垂直方向梯度

3.6 磁场梯度

通过观察图11、图12，发现磁场梯度与电场梯度类似，没有明显的单调性，同样不适合作测距的特征量。

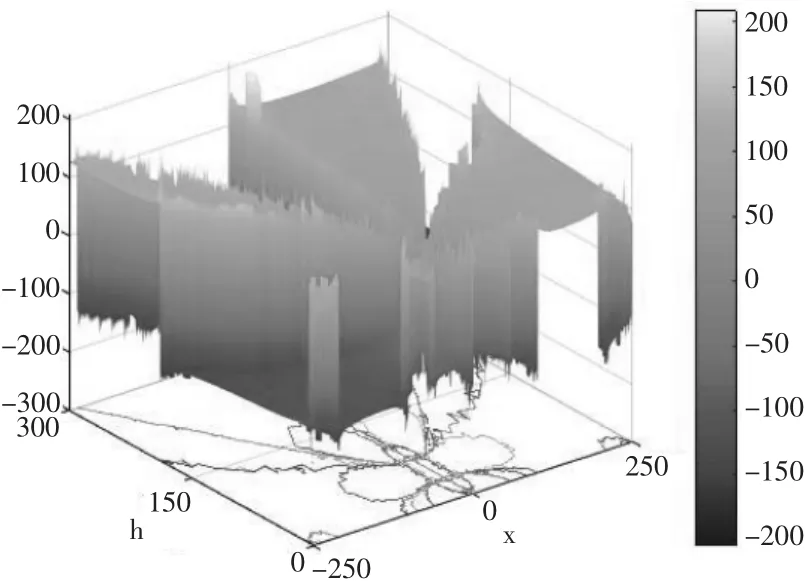
图11 电场水平方向梯度

图12 磁场垂直方向梯度

3.7 不同高度下的电场值

通过3.3-3.5节计算发现，目前单一的电场、磁场及电场、磁场梯度在正负半轴两侧都没有严格的单调性，因此无法作为距离的有效特征量。但观察图2—图4发现电场值虽在正负半轴两侧没有严格单调，但在不同高度，电场值是随着距离增加单调减小的；观察图5、图6的磁场分布可以得到相似结论。

因此，可以通过不同高度的电场或磁场值作为判断输电线路距离的特征量。由于线路周边的磁场和线路负荷的密切相关，因此采用电场能更好的反映无人机测点和线路的距离。同时电场的有效值测量更为方便，因此可采用不同高度下电场有效值作为反应无人机和线路的距离的特征量。图13是不同高度下电场的分布图。由图可知在不同高度下，电场强度随水平距离的变化是单调的（除去观察点在杆塔区域的情况），因此结合电场强度和高度检测是有效的检测观察点离输电线距离的方法。实际中，可以先通过仿真测试得到典型杆塔不同高度下电场分布曲线，测距时再利用插值方法预测观察点离输电线的距离。如水平高度为60 m时，测得的电场值为24 675 V/m，则对应图13中的A点，其距离杆塔中心为25 m；水平高度为30 m时，测得的电场值为6 989 V/m，则对应图13中的B点，其距离杆塔中心为35 m。测距系统精度主要受电场传感器、仿真建模精度、高度测试精度的影响，总体误差可控制在0.5 m以内。

图13 不同高度下电场有效值

4 结语

本文基于有限元算法及ANSYS软件建立了特高压架空线路的电磁仿真模型，计算了输电线路周边区域电场有效值、电场分量、磁场有效值、磁场分量、电场梯度、磁场梯度等参数的分布规律，分析了电磁分量与导线距离的关系，提出了选用电场有效值结合高度来确定无人机与输电线路真实距离的方法。可为输电线路无人机巡检距离检测、航向规划、避障设计提供参考。