基于粒子群优化算法的特高压输电线路覆冰不平衡张力计算
2019-04-02吴俊俊卢彬芳
吴俊俊,宋 刚,卢彬芳
(中国能源建设集团浙江省电力设计院有限公司,杭州 310012)
0 引言
输电线路架线完成后由于气象条件变化、导线塑性伸长等原因,线路各档应力出现变化,导致各档应力不同,悬垂绝缘子串出现倾斜偏移,杆塔承受不平衡张力,在线路不均匀覆冰情况下不平衡张力尤其显著。特别在经历了2008年冰灾后,设计人员对事故倒塔段进行计算分析,发现倒塔主要原因是输电线路覆冰不均匀造成杆塔纵向张力差大于设计耐受值[1-2]。因此输电线路铁塔不平衡张力取值对输电线路优化设计和安全运行具有重要意义。
设计规程[3]规定了对不同冰区线路铁塔设计最大不平衡张力百分数的下限值。由于实际线路的档距、高差、覆冰情况的复杂性,为了校验杆塔强度、对地距离等设计参数,必须根据耐张段实际情况求解覆冰不平衡张力。不平衡张力计算的数学模型为高维非线性方程组,一般采用“试凑法”[4-7]求解,也有采用牛顿法[8]、置信域算法[9]和有限元方法分析[10-11]。试凑法、牛顿法求解与初值取值、迭代步长等相关,容易出现无解状况;置信域算法和有限元方法虽能收敛得到最优解,但算法复杂,设置参数多,且迭代次数较多。本文采用算法简单、设置参数少、迭代次数少、收敛性强的PSO(粒子群优化算法)进行求解,并通过具体算例验证模型和算法的准确性。
1 计算模型
架设一个耐张段内有n个连续档,n-1基直线塔,架线气温为tm,导、地线初伸长尚未放出时架线应力为σm,各直线杆塔上悬垂绝缘子串均处于中垂位置。当出现不均匀覆冰时,各档应力不一,悬垂串发生偏移,档距发生变化,如图1所示。

图1 连续档受不平衡张力示意
第i档档距增量Δli与档内应力σi间的关系式如下:

式中:li为耐张段内悬垂串处于中垂位置时第i档的档距;βi为高差角;α为导线的温度线膨胀系数;E为弹性系数;tm为导线架线时气温;σm为相应气温下耐张段内的架线水平应力;Δte为架线时考虑初伸长降低的等效温度(取正值);γm为架线时导线的自重比载;t为计算不平衡张力时气温;σi为第i档的水平应力;γi为比载;Δli为档距增量(缩短时为负值)。
由于待求情况下各档水平应力不同导致相邻档间悬垂串出现不平衡张力差,使悬垂串出现偏斜,如图2所示。
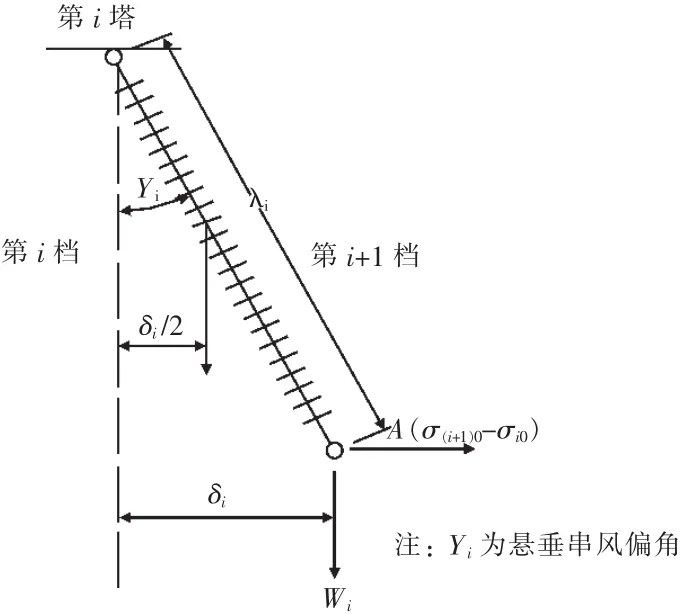
图2 悬垂绝缘子串受力偏斜图
第i基直线塔上悬垂串末端导线悬挂点的顺线路水平偏移δi与两侧导线张力差的关系为:
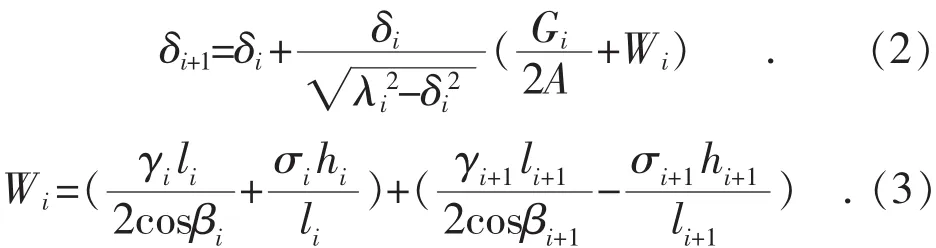
通过式(2)、 式(3)解出的 σi+1显函数为:

式中:Wi为导线重力;σi,σi+1分别为第i及i+1档的水平应力;δi为第i基直线塔悬垂串导线悬挂点顺线路水平偏距,偏向大号为正,反之为负, δi=Δl1+Δl2+…+Δli; λi为第 i基直线塔悬垂串串长;Gi为荷载;hi为悬垂串处于中垂位置时,第i基对第i-1基和第i+1基对第i基直线塔上导线悬挂点间的高差;hi+1大号比小号杆塔悬挂点高者h为正值,反之为负值;βi,βi+1分别为悬垂串处于中垂位置时,第i及i+1档导线悬挂点间的高差角,; li, li+1分别为悬垂串处于中垂位置时,第i及i+1档的档距;A为导线截面积。
对于整个耐张段内,各档档距增量之和应为零,即第n基耐张塔上导线悬挂点的偏距应为零,即:

利用式(1)可以列出n个方程,式(4)可以列出n-1个方程,式(5)可以列出1个方程,共2n个方程,有Δli,σi共2n个未知数,因此该模型在数学上是封闭的。模型可以简记为:

式中:x为N维变量列向量;F(x)为方程组的N维函数列向量。
求解以上方程的一般方法是“试凑法”。该方法假设第一档导线张力已知,依次求取后续悬垂串偏移和导线张力,通过迭代直至最后一基塔绝缘子串偏移为零。该方法存在的主要问题是收敛性差,初值、迭代步长的微小变化将引起解的剧烈变动[9],特别是悬垂串越短、覆冰越厚、档距数量越多等情况越难收敛。
2 算法
从计算模型可知,求解不平衡张力就是解高维非线性方程组。非线性方程组的求解问题等价于:

式中:f(x)为优化问题的目标函数。
求解上述问题的数值计算方法主要有Gauss-Newton法、Levenberg-Marquardt法和置信域算法[9]等。几种算法都需要对方程进行求导,对复杂的方程组来说十分困难。PSO最早是由Eberhart和Kennedy于1995年提出的一种基于群智能方法的演化计算技术,它的基本概念源于对人工生命和鸟群捕食行为的研究,在工程领域应用广泛[12-15]。文献[16-18]说明了采用粒子群优化算法在配电网规划、无功优化、发电机组出力调节等方面的应用,很好的解决工程应用问题。通过在解空间追随最优的粒子进行搜索,具有算法简单、设置参数少、收敛性强的优点。
算法原理如下:首先初始化一群随机粒子,然后通过进化(迭代)找到最优解。每个粒子通过跟踪个体极值pBest和全局极值gBest来寻找最优解。数学描述为:设在一个n维的搜索空间中,由m个粒子组成的种群X={x1,…,xi,…,xm}, 其中第 i个粒子位置为 xi=(xi1, xi2, …, xin)T,其速度为 vi=(vi1, vi2, …, vin)T。 它的个体极值为pi=(pi1, pi2, …, pin)T, 种群的全局极值为 pg=(pg1,pg2, …, pgn)T, 粒子 xi将按式(8)、 (9)改变自己的速度和位置。

式中:d=1,2,…,n,n为粒子维度;i=1,2,…,m,m为种群规模;t为当前进化代数;r1和r2为分布于[0,1]之间的随机数;w为惯性权重因子;c1和c2为加速常数。
从式(8)中可知,每个粒子的速度由三部分组成:第一部分为粒子先前的速度;第二部分为“认知”部分,表示粒子自身的思考;第三部分为“社会”部分,表示粒子间的信息共享与相互合作[15]。
将PSO应用于输电线路覆冰不平衡张力计算时,以绝缘子偏移δi作为求解粒子,最后一基耐张塔绝缘子偏移取δn=0,通过δi求取Δli。

通过式(1)可解出 δi关于 Δli的显函数:

将式(4)方程表示为:

将式(11)带入上式,可以得到只关于变量绝缘子偏移δ的函数,可将不平衡张力计算的未知数由2n个减少为(n-1)个,简化了方程式。
设定优化问题目标函数为:

具体步骤如下。
步骤1:初始化,设定惯性权重因子w、加速常数c1和c2,最大进化代数Tmax,将当前进化代数置为 t=1,随机产生 m个粒子x1,x2,…,xm,组成初始种群X(t);随机产生每个粒子的初始位置(δ1, δ2, …, δn)和初始速度(v1,v2,…, vn),组成位置矩阵 P(t)和速度矩阵 V(t)。
步骤 2: 根据式(13)评价种群 X(t), 计算每个粒子的适应值。
步骤3:比较粒子的适应值和自身最优值pBest。如果当前值比pBest更优,则置pBest为当前值,并设pBest位置为n维空间中的当前位置。
步骤4:比较粒子适应值与全局最优值。如果当前值比gBest更优,则置gBest为当前值,并设gBest位置为n维空间中的当前位置。
步骤5:按式(8)和式(9)更新粒子的位移方向和步长,产生新种群X(t+1)。
步骤6:检查结束条件,若满足,则结束寻优;否则,t=t+1,转至步骤2。结束条件为寻优达到最大进化代数Tmax,或评价值小于给定精度。
3 算例
3.1 计算条件
计算耐张段共7档,每档档距为500 m,除第4基直线塔有50 m高差外,其余塔等高;前4档距覆冰率为100%,后3档覆冰率根据设计规程规定取20%,如图3所示。
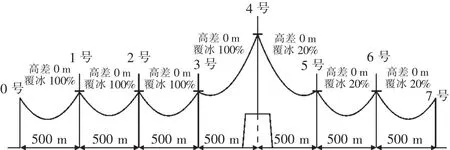
图3 连续7档模型
该耐张段气象条件如表1所示。

表1 输电线路不同工况下的气象条件
导线采用8分裂JL/G1A-500/45钢芯铝绞线,地线采用JLB20A-170铝包钢绞线。导地线参数见表2。

表2 导地线参数
导线安全系数取2.5,地线安全系数取4.2,架线气温取15℃,导线初伸长降温取25℃,地线初伸长降温取10℃。架线完成时悬垂串无偏斜。
导线悬垂串长11 m,串重取650 kg,地线悬垂串长取0.75 m,串重取30 kg。
3.2 计算结果
编程实现以上数学模型的算法,得到导、地线覆冰不平衡张力计算结果见表3。其中不平衡张力百分比为铁塔两侧张力差与最大使用张力的比值。
3.3 影响因素
影响覆冰不平衡张力的因素有很多,比如档距、高差等[9,19],研究这些因素对不平衡张力的影响程度,明确哪些是主要控制因素对覆冰地区输电线路设计具有重大意义。
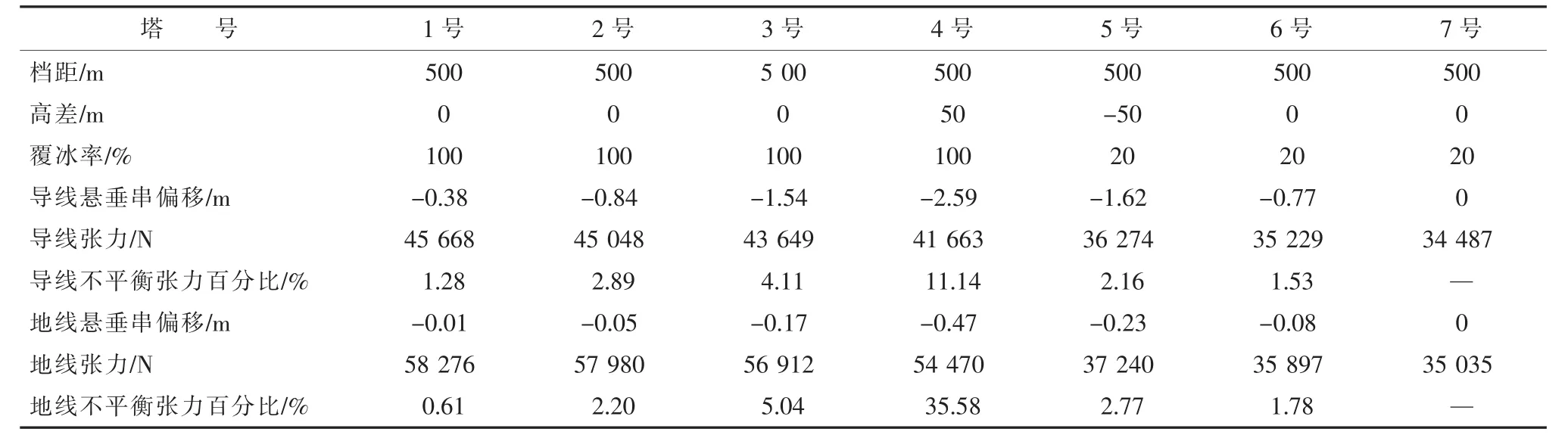
表3 不平衡张力计算结果
下面以导线覆冰不平衡张力计算为例,其它条件不变,表4为仅改变档距大小的不平衡张力计算结果,表5为仅改变高差的计算结果,表6为改变安全系数的计算结果,表7为改变悬垂串长的计算结果。从这几张表中可以看出这些影响因素的改变对不平衡张力的影响。
从计算结果可知,除了导线安全系数对不平衡张力计算结果影响不大外,档距、高差、串长对不平衡张力影响均较大。总结规律如下:
(1)档距越大,覆冰不平衡张力越大。杆塔两侧大档距比一侧大档距一侧小档距不平衡张力大,选线时应尽量避免大档距,特别是避免连续大档距的出现。
(2)高差越大,覆冰不平衡张力越大。选线时应尽量避免大高差的档距出现。
(3)悬垂串越短,覆冰不平衡张力越大。不平衡张力百分比增大幅度大于串长减小幅度。设计铁塔地线支架时应考虑可使用长地线串,减小不平衡张力。
4 结语
针对输电线路覆冰不平衡张力模型的高维非线性的特点,采用粒子群优化算法进行计算,避免了求导等复杂计算程序,设置参数少,收敛性强,并且验证了模型和算法的准确性。通过改变档距、高差、安全系数和悬垂串长等,计算几种因素对覆冰张力的影响,指导设计降低不平衡张力的一些措施;同时对线路覆冰耐张度进行定量计算,为铁塔抗冰设计和安全运行提供依据,避免出现不均匀覆冰倒塔事故。
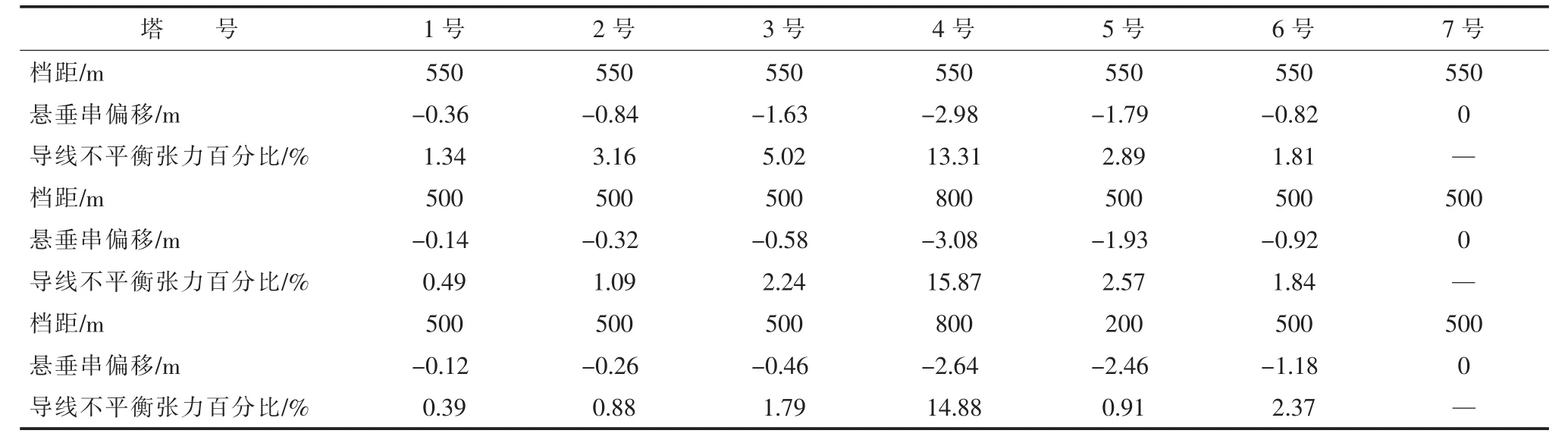
表4 改变档距不平衡张力计算结果

表5 改变高差不平衡张力计算结果
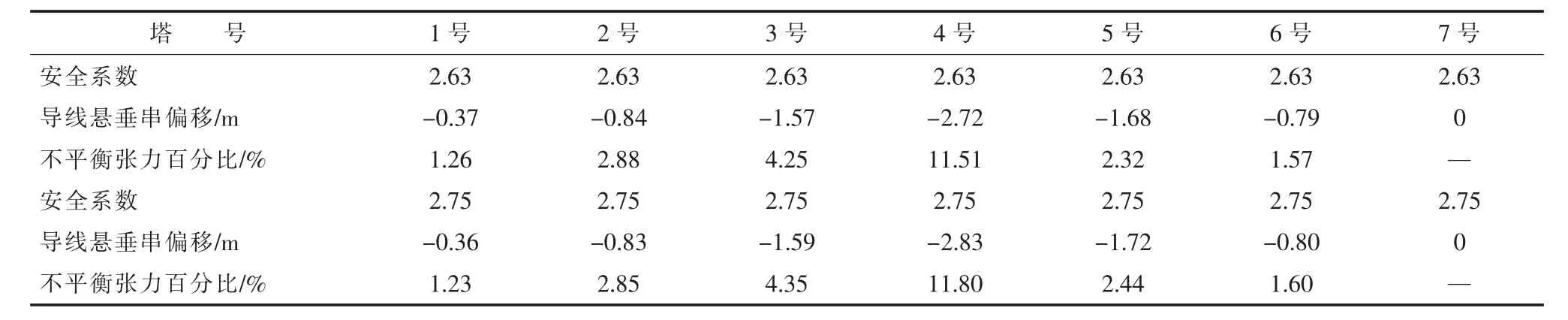
表6 改变安全系数不平衡张力计算结果

表7 改变串长不平衡张力计算结果
