基于北斗Ka星间链路的地面用户导航方法
2019-04-02李理敏常家超余金培龚文斌
肖 洋,李理敏,常家超,余金培,龚文斌,梁 广
(1. 中国科学院上海微系统与信息技术研究所,上海 200050;2. 中国科学院大学,北京 100049;3. 上海微小卫星工程中心,上海 201203;4. 温州大学数理与电子信息工程学院,温州 325035)
0 引 言
精度、完好性、连续性和可用性是全球卫星导航系统的四大关键指标[1]。其中,可用性是指导航系统的用户可以根据接收的导航信号获取自己的位置信息。传统的L频段导航信号容易受到各种有意或者无意的干扰和欺骗[2-5],尤其是一些重点区域和敏感区域,在特殊时期将会成为各种干扰源与欺骗源的攻击目标,导致L频段导航信号在该区域导航性能下降甚至失效,严重威胁地面用户的安全。
北斗卫星导航系统是我国自主建设、独立运行,并与世界其他卫星导航系统兼容共用的全球卫星导航系统。北斗导航系统设计了基于Ka频段的星间链路网络,可完成星间、星地高精度双向测量,并具有一定的数据传输能力,已成功应用于北斗导航星座的自主运行及测控管理[6-10],利用其富裕资源为地面L频段导航信号失效区域提供导航定位服务具有重要意义:一方面能避开针对L频段导航信号的干扰和欺骗,有效弥补L频段导航信号失效带来的缺失,另一方面北斗Ka星间链路信号载波频率高,信号传输几乎不受电离层影响[11],因此可提供精度更高的测距值。
本文首先对利用北斗星间链路信号为地面特定区域提供导航服务进行了可行性分析;然后给出了地面用户基于北斗星间链路信号的测距模型;针对时分体制下测距值时间不同步的问题,提出借助惯导信息以及用户钟差模型对测距值进行历元归算,并在此基础上推导了基于北斗星间链路信号的实时定位算法,最后通过仿真分析验证了算法的性能。
1 可行性分析
北斗星间链路采用时分体制[12-13],每颗卫星按照预定路由规划表在不同时隙通过调整其相控阵天线波束指向与其他卫星或地面站构建星间、星地链路[14]。假设T1~T5分别代表五个连续的时隙,表1为北斗卫星路由规划表示例。其中Si代表卫星号,S代表地面站,符号‘-’表示该时隙为空闲时隙。图1给出了卫星S1按照表1所示的路由规划表先后与卫星S7、地面站S以及卫星S3的建链过程。
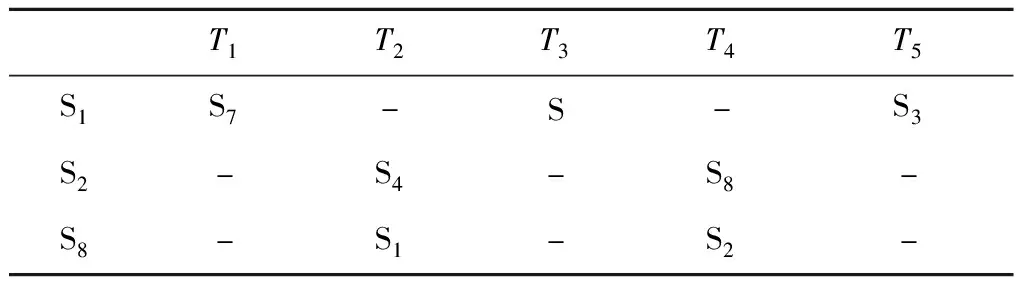
表1 北斗星间链路路由规划表示例Table 1 An example for the Routing table of Beidou inter-satellite links
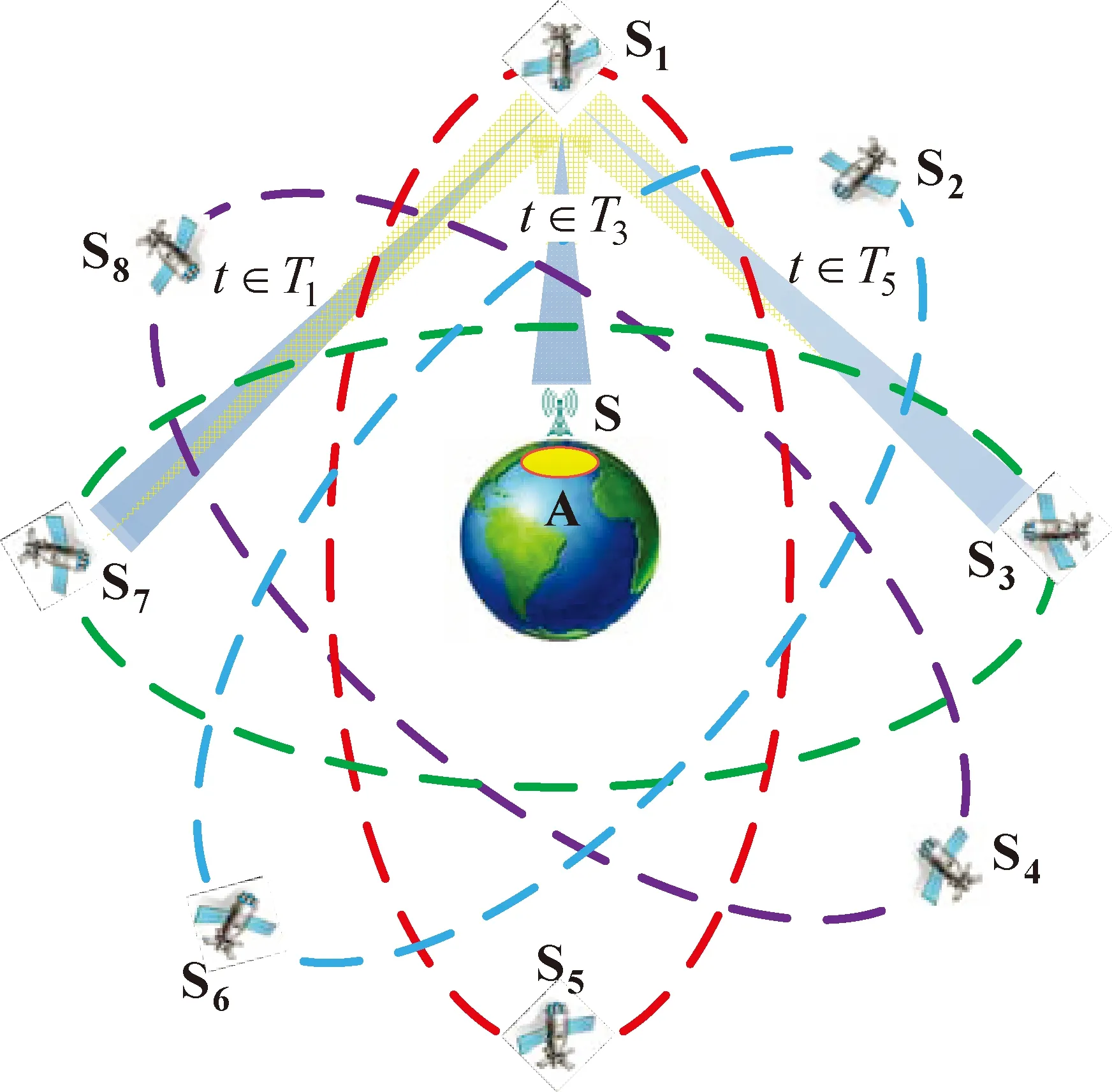
图1 北斗星间链路时分体制下星间、星地双向测量
在现有体制下,北斗星间链路仍有比较充裕的空闲时隙。假如地面A区域L频段导航信号失效,A区域内的用户通过地面应急通信方式将该区域位置告知地面主控站S,S随即重新规划星间链路路由规划表,并将其上注至视线范围内的北斗卫星S1,S1利用北斗星间链路的通信功能将新的路由规划表广播至所有北斗卫星。根据表1可知,其上空的卫星S8、S1、S2分别在时隙T1、T2、T3空闲。因此,在星间链路路由规划表中将卫星S8、S1、S2的波束分别在时隙T1、T2、T3指向区域A,并广播下发星间路由规划表信息,如图2所示。对于失效区域A内的地面用户来说,可通过两种方式来调整自己的天线指向以便对准目标卫星:1)当地面应急通信系统可用时,可通过地面应急通信系统获取北斗卫星的相关信息;2)当地面应急通信系统不可用时,地面用户可根据预先内置或导航失效前获取的卫星历书信息,调整波束跟随指向视线范围内的某颗北斗卫星直至收到其信号,并获取其下发的星间路由规划表信息。因此,利用北斗星间链路的空余时隙为地面用户提供导航服务是可行的。
2 基于北斗Ka星间链路的用户测距模型
假设在Tk-1与Tk两个历元之间,地面某区域装载有北斗星间链路终端的用户分别在不同时刻与不同N颗北斗卫星产生星间链路单向测距值,测距方

图2 利用北斗星间链路空余时隙服务于地面区域
程为
(1)

(2)
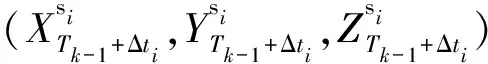
b(t)=a0+a1t+ε
(3)
式中,b(t)代表接收机钟差,a0代表接收机钟差初始值,a1代表接收机钟飘,ε可视为零均值高斯白噪声,因此有
bTk-1+Δti≈bTk-a1,Tk(Tk-Tk-1-Δti)
(4)
利用惯导系统可以得到用户从Tk-1+Δti时刻到Tk时刻的位置变化量为

(5)
式中:
(6)
式中,Vx(t)、Vy(t)、Vz(t)分别代表用户的三维速度。将式(4)和式(5)代入到式(1)和式(2),即可将观测方程中用户的位置统一归算到Tk时刻,从而实现测距值时间同步,如式(7)和式(8)所示,其中对流层延时使用高精度模型予以校正。
(8)
由于对流层模型存在误差,且历元归算过程也会引入误差,因此式(7)中的误差项用νi来表示。由于广播星历广播的是L链路信号对应的天线相位中心位置及通道时延,当地面用户使用基于北斗Ka星间链路测距值定位时,将存在天线相位中心偏差、通道时延偏差等系统偏差[15-16]。为了消除这些系统偏差对定位结果的影响,可预先在地面对其标定或者星上实时标定然后下发给地面用户,本文暂不考虑这些系统偏差对定位结果的影响。
3 基于北斗Ka星间链路地面用户定位算法
在实现测距值时间同步的基础上,地面用户即可采用卡尔曼滤波定位算法实时估算自己的位置,选取的状态量为
(9)
式中:δr代表对地面用户三维位置估计的偏差,δv代表对地面用户三维速度估计的偏差,δb代表对接收机钟差、钟飘估计的偏差。与δr、δv相关的状态转移矩阵Φrv为
(10)
式中:Δt代表历元间隔时间,与δb相关的状态转移矩阵为
(11)
因此,系统状态转移矩阵Φk,k-1为
(12)
式中:0m×n代表m×n阶零矩阵,系统过程方程为
xk=Φk,k-1xk-1+wk-1
(13)
式中:下标“k”代表历元时刻,wk-1代表过程噪声,系统观测方程为
yk=Hkxk+vk
(14)
式中:Hk为观测矩阵,可由式来描述,yk为观测量,可由式(17)来描述,vk为观测噪声。
Hk=
(15)
式中:
(16)
(17)

(18)
(19)
式中:右上标“-”和“+”分别表示对状态量估计的先验值和后验值,Qk-1为过程噪声的协方差矩阵。
在更新步骤,状态量及其协方差矩阵变化为
(20)
(21)
(22)
式中:Kk为卡尔曼滤波增益,Rk为过程噪声的协方差矩阵。
4 算法性能仿真
利用轨迹发生器产生的数据对上述算法进行性能初步仿真。仿真轨迹如图3所示,载体初始位置设为东经110°、北纬30°、高度为0 m,初始横滚角、俯仰角、航向角均为0°,在东向、北向和天向的初始速度均为0 m/s,为不失一般性,载体运动轨迹包括匀加速直线运动、匀速直线运动、爬升、等高转弯、俯冲等过程,仿真时间为3 600 s。假设惯导系统中三个陀螺仪零偏均为0.1(°)/h,随机漂移均为0.1(°)/h,三个加速度计的零偏均为10-4g,随机漂移均为10-4g,接收机时钟随机误差设为0.1 m。对流层模型误差设为0.5 m,使用精密星历(包括精密轨道星历和精密钟差星历)来模拟测距值,实际定位过程中使用广播星历,Ka频段测距误差为0.1 m[6]。

图3 地面用户轨迹仿真
使用STK软件对北斗星座进行轨道仿真,当遮蔽角取15°时,可见星数目为6~10颗。设历元间隔Δt为30 s,假定在每个历元间隔内所有可见星都可以指向地面一次。在相同可见星以及对流层模型误差情况下,将本文算法与传统基于L频段信号的定位算法进行比较,设L频段测距误差为0.8 m(已通过双频组合消除电离层影响)。两种算法在导航坐标系中北、东、地三个方向误差曲线分别如图4~图6所示,三维位置误差曲线如图7所示。L频段定位算法在北、东、地三个方向的误差分别为0.86、0.72、1.58 m,三维位置误差为1.94 m,本文算法在北、东、地三个方向误差分别为0.79、0.60、1.44 m,分别提高了8%、16%、9%,三维位置误差为1.75 m,提高了10%。

图4 两种算法北向误差曲线
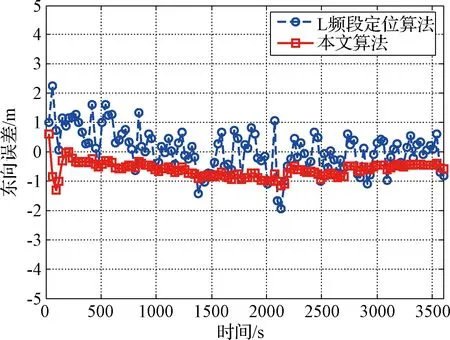
图5 两种算法东向误差曲线

图6 两种算法地向误差曲线

图7 两种算法三维位置误差曲线
为了评估接收机时钟随机误差对定位性能的影响,图8给出了两种算法在不同时钟随机误差条件下的三维位置误差曲线。由图8可知,当时钟随机误差较小时,本文算法定位误差小于L频段定位算法;随着时钟随机误差增大,本文算法定位误差明显增加。因为当时钟误差较小时,其对历元归算过程影响并不明显,此时测距误差是影响定位精度的主要因素;随着时钟误差的增加,会导致本文算法观测值历元归算准确性下降,从而使得本文算法对时钟误差更为敏感。
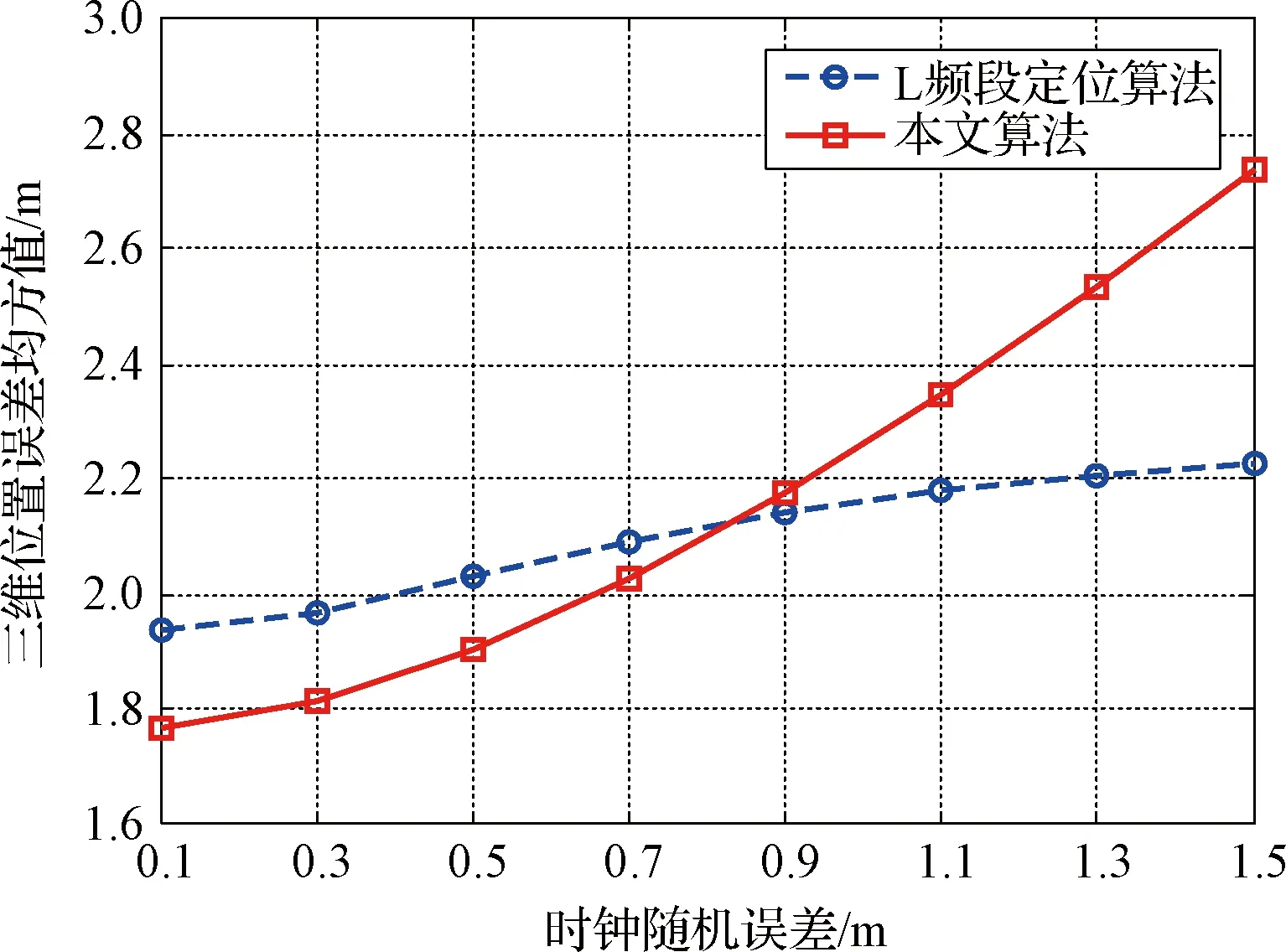
图8 两种算法在不同时钟误差下的三维位置误差曲线
为了评估历元间隔对定位性能的影响,表2给出了两种算法在历元间隔分别为30、60、120 s情况下的定位误差。由表2可知,当历元间隔增大时,两种算法定位误差均呈上升趋势。相比之下,本文算法随历元间隔增大性能下降更加明显,当历元间隔为120 s时,L频段定位算法三维位置误差增加到2.13 m,而本文算法三维位置误差增加到3.25 m。另一方面,历元间隔增大的同时也会降低对星间链路空闲时隙的消耗。因此,实际情况中需要综合考虑历元间隔对定位性能以及星间链路时间资源消耗的影响。
为了评估惯导系统误差参数对定位性能的影响,表3给出了两种算法在初始值和20倍初始值这两种情况下的定位误差。由表3可知,当惯导系统误差参数增加为原来20倍后,L频段定位算法在北、东、地三个方向上的误差分别增加了5%、4%、2%,三维位置误差增加了3%;而本文算法在北、东、地三个方向上的误差分别增加了15%、18%、37%,三维位置误差增加了30%。由于惯导系统误差参数同样会影响过程噪声以及历元归算误差,因此,相比之下本文算法对惯导系统误差参数更加敏感。
在上述仿真过程中,链路数目与可见星数目保持一致,即6~10条。为了评估链路数目对算法性能的影响,表4给出了两种算法在链路数目分别为6~10条、只选6条、只选5条三种情况下的定位误差。由表4可知,当链路数目减少时,由于观测量数目减小,L频段定位算法与本文算法定位精度均有所下降。因此,为了提高定位精度,应尽可能为地面用户分配更多的链路。

表2 不同历元间隔定位误差均方值Table 2 The root-mean-square (RMS) of position errors with different epoch intervals (m)

表3 不同惯导系统误差参数定位误差均方值Table 3 The RMS of position errors with different error parameters of INS (m)

表4 不同链路数目下定位误差均方值Table 4 The RMS of position errors with different number of links (m)
5 结 论
本文根据北斗Ka星间链路的特点,提出了一种利用星间链路信号为地面L频段导航信号失效区域提供导航定位服务的方法。利用钟差模型和惯导系统解决测距值时间不同步的问题,并在此基础上推导了基于北斗Ka星间链路信号的实时定位算法。仿真结果表明:当历元间隔为30 s时,本文算法定位精度可以达到2.0 m以内。与此同时,本文还详细分析了接收机时钟随机误差、历元间隔、惯导系统误差和链路数目等因素对算法定位性能的影响。本文方法能够在一定程度上弥补L频段导航信号失效带来的可用性问题,保障重点区域在特殊场景下的导航安全。
