基于导航定位原理的火箭涡轮泵轴承故障诊断

戴屹梅，张和生，方 柯

(北京交通大学电气工程学院，北京 100044)

0 引 言

滚动轴承是火箭涡轮泵的关键部件，与普通民用轴承相比，火箭发动机涡轮泵的轴承采用固体润滑，当轴承瞬间受到外力时易导致结构破坏，或瞬间干摩擦引起烧蚀。其故障模式体现在振动信号上的特点是：1) 振动数据中同时含有低频成分和几万赫兹量级的高频成分；2) 轴承故障特征频率振动量级小，容易被复杂的背景信号淹没；3) 轴承表面一旦出现故障，其劣化速度很快；4)振动信号中故障特征频率具有很强的突发性。这些特点使传统的振动信号分析方法不能完全适用于火箭发动机涡轮泵轴承故障特征提取。因此，如何准确地实现液体火箭发动机低温高速轴承的故障特征提取成为相关领域亟待解决的问题。

轴承DN(轴承内径与轴转速的乘积)值是轴承技术水平的主要指标，DN值越大，研制难度越高，从设计技术、材料技术、加工技术、试验技术等各方面都要面临很高的要求。高DN值轴承技术水平的限制，将会极大地制约发动机性能的进一步提升，高DN值轴承的研制需要充分的试验验证能力，因此设计具有超高速采样频率的高速轴承试验台是实现轴承研制目标的重要基础，同时需要提高轴承的早期故障诊断能力。

高能振动可能会对其他部件造成损害,并由此产生新的振动频率信号。这意味着多个振动频率之间可能存在因果关系。因此,也有必要判断不同振动频率发生的时间顺序,以找出它们之间可能的因果关系,用于振动信号的故障诊断。

提高这些能力需要探讨新的理论途径,进行跨专业的技术创新，为新型的高速低温轴承试验台设计寻求理论支撑。

常用的涡轮泵轴承故障诊断方法是利用振动信号、声学信号、温度信号和介质参数变化量等对故障进行预警[1-3]。振动参数作为液体火箭发动机的重要参数应用于故障诊断工作中，源于航天飞机主发动机(SSME)的研制初期[4]。文献[5]是NASA/马歇尔空间飞行中心研究人员提出的一种CPLE分析方法，CPLE技术可以做出一种能够同时保留振幅和相位的二维频谱，这在传统的频谱分析中是不可能实现的。

安塔瑞斯(Antares)130 首飞失败，一级火箭的两台AJ-26发动机点火15 s 涡轮泵发生故障，E15发动机氧泵转子与静子发生碰磨，产生火花点燃液氧导致泵爆炸。专家认为，如果能对飞行前的振动试验数据发现的异常频率信号进行振源位置定位，完全有可能避免这次重大失败。

为了对故障进行诊断，近些年来出现了大量的分析动态非平稳信号的方法，比如短时傅里叶变换[6]，Wigner-Ville分布[7]，小波变换[8]，EMD分解法[9]，随机共振[10]小波阈值降噪[11]等。形态滤波器(MF)是一种时域算法，能够直接提取冲击特性的几何结构[12]。文献[13]介绍了一种改进的MF，该方法能够从低信噪比信号中提取故障特性。文献[14-18]介绍了几种先进的时频分析技术并将其应用到轴承故障诊断上。

由于轴承的过度疲劳使用,轴承部件中往往发生剥落,如保持架、外圈、内圈、滚动体等,因此滚动轴承中遇到的故障类型为保持架故障、外圈故障、内圈故障、滚动体故障[19]。故障诊断的关键步骤是从振动信号中提取故障特征频率，传统的方法是对实测的频率分量和理论计算值进行比较。由于滑动和滚动接触,实测值与理论计算结果不完全相等,有约 5%～10% 的差异。另一方面,由于振动传感器能够准确获得机械设备的工作信号,这些信号不仅包含一些显示机器健康状况的信息,而且还含有一些无用的噪音和干扰信号,比如来自齿轮箱和环境等的振动信号。在复杂的机械系统中,这些方法具有一定的内在制约，轴承元件的特征频率往往与变速箱或其它部件的特征频率非常接近,这就很难完全依靠特征频率对故障进行准确的判断。因此,能够准确找到振源位置是故障诊断的终极方法。

振源定位法思路清晰，方法简便，具有通用性。但是定位精度低，要想提高精度，必须提高振动信号频率，提高时延估算精度，因此出现了各种超声波定位仪器，包括医学上使用的超声波检查设备。火箭发动轴承的转速一般为数万转，最高可达8万转，其故障特征频率小于6 kHz。这样的频率，用传统的时延估计算法[20]，其精度无法达到故障定位要求。

根据文献[21] 推导出的时幅曲线表达式：

因此，从理论上讲，可以通过不同位置的振动传感器测得的同一个突发振动信号的相位差来计算出振源的位置。基于这一点，本文提出一种新的突变信号轴承故障诊断方法，将信号处理技术和卫星导航定位原理相结合，发挥二者的优点。此方法类似于定位算法，即将四个振动传感器和被测轴承设计在一个与卫星导航定位WGS-84类似的直角坐标系中，将系统采样频率提高到128 MHz以上，利用时幅曲线分析法精确捕获故障频率在各传感器的出现时刻，将此时间作为输入条件，计算振动波源位置，进而判断出轴承故障。

为了表述严谨和简洁，本文提出一个理想模型，在工程应用中，可以利用该文给出的方法，根据精度要求设计不同的实施方案。在实际工程中，多个振动之间往往存在因果关系。因而，利用振动信号进行故障诊断，同样需要判断不同振动出现的先后顺序，寻找它们之间的因果关系及引起故障的原因。

1 系统构成

任何一次振动均包含四个要素：振源位置、振动强度(幅值)、振动发生的时间、振动频率。了解这四个要素是彻底了解一次振动的必要条件。从振动数据中提取四个要素中的某一个或几个，称之为振动信号特征提取，用提取的特征信号进行故障诊断还需要其他相关知识的配合。目前，对于轴承振动数据的故障特征提取基本集中在特征频率，振动幅值和振动发生的时间方面，对于确定振源位置几乎没有涉及，这是因为火箭发动机涡轮泵轴承的最高转速为8万转/分量级，振动信号频率远远达不到超声波量级，如果没有相位信息，几乎无法达到定位所需求的毫米级精度。

对于氢氧火箭发动机涡轮泵高速轴承试验台，在试验时将轴承置于液氮冷却箱中，试验台的这一结构特点使得在轴承周围分布多个振动测点成为可能。将试验系统在结构上按图1设计，利用振动定位算法与高速采样同步测控技术以及时幅拐点数值分析方法相结合对轴承故障点进行诊断定位。

图1 系统坐标系及轴承传感器结构布局示意图

以轴承的几何中心为坐标原点，传动轴的轴线为X坐标轴，垂直向上为Y轴，垂直向外为Z轴，建立立体直角坐标系。振动传感器1，2，3，4分布在以R为半径、以轴承的几何中心为圆心的球面上。振动传感器1，2，3，4的坐标分别为1(R,0,0)，2(0,-R,0)，3(0,R,0)，4(0,0,R)。

2 空间坐标定位原理

2.1 空间坐标定位数学模型

设4个振动传感器测得同一振动的时刻分别为t1，t2，t3，t4，振动波在冷却液中传播速度为V，振源的坐标为(X,Y,Z)，4个传感器的坐标为(Xi,Yi,Zi)，i=1,2,3,4，则各传感器与振源之间的距离为

设各个传感器测得同一振动信号的时刻为ti(i=1,2,3,4,)，t0为距振源最近的传感器测得振动信号的时刻，则t0=min{t1,t2,t3,t4}；各个传感器测得同一振动信号的时刻与t0的时间差为Ti0=ti-t0(i=1,2,3,4,)。设T为振动从振源传到距振源最近的振动传感器所用的时间，那么

dsi=(T+Ti0)V，i=1,2,3,4，即

(1)

式中：T，X，Y，Z是需要求解的未知数。

整理原方程组(1),并将常数记为kij，则：

(2)

将前三个方程联立：

(3)

(4)

(5)

(6)

(7)

(8)

将式(8)代入式(1)整理得：

T2+k80T+k81=0

(9)

解出T，X，Y，Z，坐标(X,Y,Z)即为振动源所在位置坐标。

2.2 判定故障部位数学模型

根据振源坐标(X,Y,Z)判定故障部位方法。

图2是轴承在坐标系中的位置图和其尺寸说明。设轴承内圈内径为2r1，内圈外径为2r2，外圈内径为2r3，外圈外径为2r4，轴承座外径为2r5，轴承宽度为h。

图2 轴承各部件在坐标系中占据的空间位置图

不难看出，通过坐标(X,Y,Z)的值可以判定故障所在部位。

1)轴承座所占据的坐标空间同时满足以下数学表达式：

(10)

2)轴承内圈所占据的坐标空间同时满足以下数学表达式：

(11)

3)轴承外圈所占据的坐标空间同时满足以下数学表达式：

(12)

4)轴承滚动体和保持架所占据的坐标空间同时满足以下数学表达式：

(13)

式(1) 和式(10)～(13) 可用于推导故障识别算法,算法流程如图3所示。

在精度较低的系统中,如果计算出的故障位置坐标位于轴承两个部件的交界面区域，则可将计算出的振源位置坐标和轴承元件的理论特征频率进行对比，对故障部位做出准确的判断。因为轴承不同部件的特征频率数值差别较大。

图3 计算振动源坐标和判断故障部位的流程图

2.3 模数转换精度和多通道同步问题

在工程上实现本文提出的方法，需要高速多通道同步采样板，采样频率大于100 MHz，通道数大于4，各通道的同步误差小于0.1 ns。以下是SPECTRUM INSTRUMENTATION公司的一款产品，M4i.44xx-x8-14/16性能完全满足要求。

四通道采样频率为500 MS/，所有通道同步采样，通道之间同步采样时间误差小于60 ps。

2.4 轴承故障信号时域波形

轴承故障信号时域波形一般较为复杂，为振荡衰减的周期信号，文献[21]做了详细的介绍。振荡衰减周期信号经过傅里叶变换，其能量大部分集中在基频正弦信号上。所以在频域提取的故障信号都是正弦信号，故障仿真信号用3589 Hz正弦信号。

2.5 坐标精度问题

本文给出的是理论直角坐标系的计算公式和故障定位判定方法，为了简化方程,便于理解,本文选取了4个特殊坐标。在实际工程实现中，四个振动传感器和轴承所占据的空间位置与理论位置存在误差。用三坐标机测量四个传感器和轴承几何中心的坐标,并根据这些测量结果再次建立较为复杂的定位方程如式(1)和四故障判断不等式如式(10)～(13)。目前,市场上三坐标机的精度可达(2.5±L/300) μm,本文取L=R=300, 所以坐标测量精度达到 3.5 μm,完全满足精度要求。

2.6 噪声的影响

真实的试验数据中包含各种噪声，为了考核噪声环境下该方法的可行性，本文采用了工程仿真的方法，构造仿真数据时域信号时，将故障信号叠加到真实的试验数据中，可最大限度模拟真实环境下的故障信号，然后再用时幅曲线拐点分析法对故障信号发生的时刻进行提取。

3 仿真校验

3.1 构造传感器仿真时域信号

(14)

设ts为振源发出振动信号的时刻，各个传感器测得信号的时刻为：

(15)

各传感器捕获到同一信号的时间差分别为

由此得出仿真程序的输入输出参数。

输入参数：(X′，Y′，Z′)，R，V，K

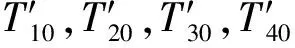
将特定频率的振动信号依据时间差加到真实的试验数据中，即可获得仿真计算所需要的时域信号试验数据。

设轴承结构参数为r1=17.5 mm，r2=21.5 mm，r3=27 mm，r4=30 mm，r5=34 mm，h=14 mm。振源坐标为(5,0,28)，位于轴承外圈区域，R=300 mm，振动波在液氮中的传播速度为V=1168000 mm/s，采样频率为k=128000000 Hz。

将以上参数输入到求解仿真参数程序，计算结果:

2.580011×10-4, 2.580011×10-4,

2.329161×10-4}=2.329161×10-4

(2.329161×10-4)=0.207875×10-4

(2.329161×10-4)=0.250850×10-4

(2.329161×10-4)=0.250850×10-4

(2.329161×10-4)=0.0×10-4

3.2 合成振动传感器故障时域信号

图4 真实试验数据时域图

图5 传感器1合成后试验数据时域信号

用同样的方法合成其余三个传感器的时域数据。

3.3 仿真计算和故障诊断

利用第3.2节合成的传感器仿真时域信号计算振源位置并进行故障诊断。

3.3.1时幅曲线拐点分析算法简介

根据参考文献[21]所介绍的时幅曲线拐点分析算法,以Δt为时间步长，信号采样频率Fs。

在(T1+nΔt，T2)时间段内逐次取信号序列fj的傅里叶变换中频率k的幅值Akn，则有

(16)

其中L为分析点数，L=N-nΔtFs；N为原序列的总采样点数，N=(T2-T1)Fs，n≤N。

只要采样频率Fs足够高,计算步长Δt足够小,就可以得到所需精度的信号出现和消失时刻。

为了直观理解该算法和时幅曲线，构造函数f0(t)

(17)

对函数f0(t)进行12800 Hz采样，取分析时间从0～15 s，其时幅曲线如图6所示。

图6 f0(t)在200 Hz的时幅曲线(0～15 s)

分析时间从0～9 s，此时时幅曲线如图7所示。

图7 f0(t)在200 Hz的时幅曲线(0～9 s)

从图6和图7可以看出,时幅分析法能够准确计算出信号的出现时刻和消失时刻。不同的分析时段对应不同的曲线形状，但信号拐点出现的时刻是不变的。

3.3.2用时幅曲线分析算法求出各传感器合成数据中3589 Hz信号出现的时刻

为了节省计算时间,先用Δt=0.001 s计算0～0.03 s时段范围内传感器1的3589 Hz时幅曲线，得到3589 Hz信号出现时刻大致在0.01 s，如图8所示。再缩小分析时段范围，在0.00975～0.01015 s之间，用Δt=1×10-8s计算3589 Hz的时幅曲线如图9～图12所示，选取幅值达到峰值时的时刻为ti(i=1,2,3,4)。

图8 0～0.03 s 3589 Hz时幅曲线

1)传感器1数据分析

从图9所示传感器1的时幅曲线可以看出，3589 Hz信号出现的时间为t1=1.000567×10-2。

图9 传感器1数据在3589 Hz的时幅曲线

2)传感器2数据分析

从图10所示传感器2的时幅曲线可以看出，3589 Hz信号出现的时间为t2=1.000825×10-2。

图10 传感器2数据在3589 Hz的时幅曲线

3)传感器3数据分析

从图11所示传感器3的时幅曲线可以看出，3589 Hz信号出现的时间为t3=1.000979×10-2。

图11 传感器3数据在3589 Hz的时幅曲线

4)传感器4数据分析

从图12所示传感器4的时幅曲线可以看出，3589 Hz信号出现的时间为t4=9.984540×10-3。

图12 传感器4数据在3589 Hz的时幅曲线

t0= min{t1，t2，t3，t4}=min{1.000567×10-2，

1.000825×10-2，1.000979×10-2，

9.984540×10-3}=9.984540×10-3

T10=t1-t0=(1.000567×10-2)-

(9.984540×10-3)=0.2113×10-4

T20=t2-t0=(1.000825×10-2)-

(9.984540×10-3)=0.2371×10-4

T30=t3-t0=(1.000825×10-2)-

(9.984540×10-3)=0.2371×10-3

T40=t2-t0=(9.984540×10-3)-

(9.984540×10-3)=0.0×10-4

3.4 利用振动定位算法对轴承故障进行定位诊断

将以上时幅曲线分析法找出的各个传感器测得3589 Hz信号出现的时刻，代入公式计算出振源坐标，判断是否是轴承故障及故障部位。图3为定位故障算法流程图。

将时间t1,t2,t3,t4输入定位算法故障诊断程序，经定位算法故障诊断程序计算,得到振源位置坐标是X=3.905743，Y=-0.902871，Z=27.395615，与轴承结构参数r1，r2，r3，r4，r5比对后判定，该振源位置位于轴承外圈区域。第3.1.2节用于构造模拟数据的振源坐标为(5，0，28),与仿真计算出的振源坐标(3.905743，-0.902871，27.395615)的最大误差为 1.1 mm (5-3.905743=1.094257)。

4 结 论

由于时幅曲线分析法能够依据采样频率精度准确找出信号发生突变的时刻，这为振源空间定位分析提供了可能。其理论定位精度只与传感器的坐标精度、采样频率和多路采样器的同步精度有关；与传感器位置、振源的位置均无关。

通过以上仿真计算，在采样频率为128 MHz，传感器的坐标误差为零、多路采样器的同步误差为零、波的传播速度为1168 m/s的条件下，最大误差为±1.1 mm。

在实际应用中，只要判定振源位置在轴承结构包络范围内，即可将故障定位于轴承；通过增加定位精度可进一步判定轴承故障的具体部位，此方法亦可与故障特征频率判别法进行相互验证。

每一个振动信号都包含四个要素，即振源位置、振动发生的时间、振动的幅值(能量)、振动的频率。掌握了这四个要素也就彻底了解了与这四个要素相关的振动。利用现代技术手段从振动信号中发掘出这四个要素是通过振动信号进行故障诊断的最根本的途径。本文利用信号时幅曲线所包含的相位信息计算振源位置就是在这一方面做的一次尝试。仿真计算结果表明该方法理论上可行，有实际工程价值。