基于回溯迭代搜索-粒子群算法的配电网无功优化研究
2019-04-01,,,,
,,,,
(中海石油(中国)有限公司天津分公司工程建设中心,天津 300459)
0 引 言
无功优化是实现电网经济调度的重要手段之一,对保障电网的电压质量,降低系统网损有着重大意义[1]。无功优化过程具有多目标、多约束、同时含有连续变量和离散变量等特点[2,3],是典型的非线性规划问题。传统的无功优化算法(如线性规划法、非线性规划法、内点法[4-6]等)对于离散变量的处理存在一定的局限性。因此,近年来国内外学者对于智能算法在无功优化中的应用研究层出不穷,如遗传算法、蚁群算法、粒子群算法(particle swarm optimization, PSO)[7-8]等。其中,粒子群算法相比其他的优化算法具有优化效率高、收敛速度快、鲁棒性强的特点,但是标准的粒子群算法容易受当前最优位置的影响,易陷入局部最优解[9]。
为了克服容易陷入局部最优解这个缺点,许多文献提出了改进的粒子群算法。文献[10]针对粒子群算法容易陷入局部最优和收敛速度较慢的缺点,提出了一种改进的粒子群优化算法,以达到降低配电网有功网损的目的。文献[11]采用多种群协同优化的方法,同时兼顾了算法全局搜索和局部搜索的能力,与常规粒子群算法相比稳定性较好。文献[12]将邻居学习策略融入粒子群优化算法的速度更新中,使用“最坏替换”策略来更新群,群中最差粒子的位置被更好的新生成的位置所取代,比传统的群更新方案具有更好的性能。文献[13]通过阿尔及利亚西部电力系统中无功功率控制为背景,提出了基于PSO的启发式算法,且算法在最小功率损耗方面有优越的表现。
回溯迭代算法作为一种类似枚举法的选优搜索法,在搜索区域缩减确定和搜索速度提升上都有良好的性能,多用于解决较为复杂、规模庞大的问题。下面利用回溯迭代算法的优点,对常规的PSO算法进行改进:将回溯迭代算法融合于粒子群速度和位置更新策略,得到一种改进的粒子群优化算法。通过在IEEE 30节点配电网进行无功优化仿真,验证该算法具有较好的全局收敛性,且可以快速准确地搜索到最优值。对比常规PSO算法,所采用的改进粒子群算法的收敛速度和精度更好,优化后有功网损值也得到改善。
1 配电网无功优化的数学模型
1.1 目标函数的构造
为了提高配电网的供电可靠性和经济性,传统无功优化通常有以下几种目标函数:1)电网有功网损最小;2)电压质量最好;3)电容器和变压器分接头投切次数最少;4)电网无功补偿容量最小;5)系统总的费用最少。
对配电网进行无功优化时,考虑全网有功网损最小,建立无功优化数学模型的目标函数为
f=minPLoss
(1)
式中,PLoss为系统有功网损。
考虑电压质量和无功补偿设备的容量限制,目标函数可改写为
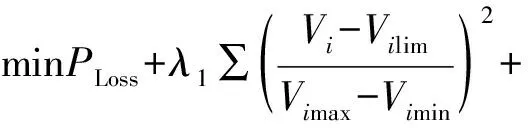
(2)
式中:Vi为节点i的运行电压;Vimax、Vimin为节点运行电压的允许上、下限;QCi为节点i的无功补偿容量;QCimax为节点无功补偿上限值;λ1、λ2分别为节点电压越限与节点无功补偿容量越限的惩罚因子。
(3)
(4)
1.2 约束条件的建立
配电网无功优化时,各节点处于功率平衡状态,其等式约束为
(5)
式中:PGi、QGi分别为节点i处发电机的有功功率和无功功率;PDi、QDi分别为节点i处负荷的有功功率和无功功率;Gij、Bij和θij分别为节点i和j之间的电导、电纳和相角差;Vi、Vj分别为节点i、j的电压。式(5)也是潮流计算的基础。
配电网中,配电网各节点电压不等式约束为
Vimin≤Vi≤Vimax
(6)
各补偿点补偿容量的不等式约束为
QCimin≤QCi≤QCimax
(7)
2 改进的粒子群算法
PSO作为一种启发式智能算法,它源于对鸟类捕食行为的研究[14]。其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解[15]。基于PSO的寻优算法流程如图1所示。
回溯迭代算法是一种选优搜索法,按选优条件向前搜索,以达到目标[16-17]。回溯迭代算法实际上是一个类似枚举法的搜索尝试过程,回溯迭代寻优过程如图2所示。图2中:A、B、C、D为步骤名称;1和0分别表示满足条件与否,当发现不满足求解条件时,就“回溯”返回,尝试别的路径。许多较为复杂、规模庞大的问题都可以使用回溯法去解决[18]。其基本思想包括以下3个特征:
1)为要解决的问题定义了解决方案;
2)确定易于搜索的解空间结构;
3)以深度优先方式搜索空间,并在搜索过程中通过剪枝函数避免无效搜索。
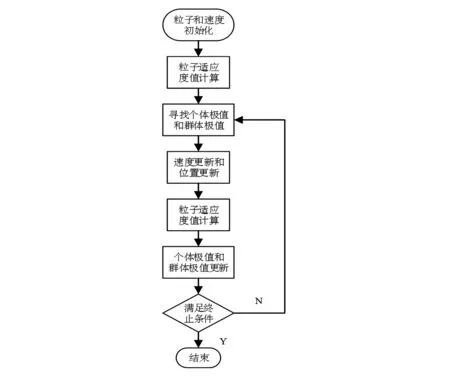
图1 标准PSO算法寻优流程
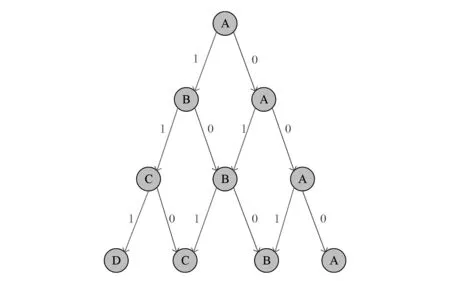
图2 回溯迭代剪枝搜索数枝
将回溯迭代算法融合于粒子群速度和位置更新策略,可以得到一种改进的粒子群优化算法即基于回朔迭代的粒子群算法(backtracking particle swarm optimization,BPSO)。该算法具有较好的全局收敛性,且可以快速准确地搜索到最优值。应用基于回溯迭代的粒子群算法解决无功优化问题,将电容器容量QC对应粒子群中粒子的位置,即Xi=QC,可行域的边界由QC的上下限确定。
3 基于回溯迭代的粒子群算法无功优化流程
运用BPSO算法求解无功优化问题的流程如图3所示,图中:Xi、Xn为每个粒子的适应值;pbest是粒子i个体经历过的最好位置;gbest是种群所经历过的最好位置。其算法具体步骤描述如下:
1)输入系统数据(系统的结构、网络数据和控制参数);
2)初始化粒子群;
3)计算目标函数值;
4)评价每一个粒子;
5)更新每一个粒子的速度和位置;
官方正式互动往往需要反复论证斟酌,耗费时间较长,相关定量分析显示,政府回应性的提升对地方政府公信力的增强有着显著的积极影响。[24] 官方正式互动的效率需要新媒体平台的即时互动强化。 即时互动能够充分发挥新媒体回应及时、交互性强等优势,政府公众号等新媒体平台应该充分利用这些优势,组建一支高素质的人员队伍,代表官方与网民进行实时互动,解答公众提出的各种问题,探知民众心态,展开有效的新媒体平台的舆情监测工作,并将信息及时向上级反映,以便及时有效地控制虚假信息的传播,进而保障政府公信力的稳定。
6)检验是否符合结束条件;

图3 BPSO算法无功优化流程
7)如果当前迭代次数达到最大预定次数(或最小误差要求),则停止迭代并输出最优解,否则将转到步骤2);
8)输出问题的解,包括系统网损值及系统最高电压值和最低电压值。
4 算例分析
采用IEEE 30算例,该系统是一个额定电压为23 kV的实际配电网系统。将系统的变电站设为0号节点,实际上该系统是一个包含31个节点、30条支路和5个无功补偿点(分别为节点13、15、19、23、24)的配电系统。系统的接线如图4所示。系统的网络参数如表1所示。
4.1 BPSO算法目标函数选取
利用Matlab7.0编写了基于BPSO的配电网无功优化计算程序。在程序中,将节点电压的上、下限设置为额定值的0.9和1.1,粒子群体规模取M=30,最大和最小惯性常数分别设置为ωmax=0.9、ωmin=0.4。将学习因子c1、c2的取值设置为c1=c2=2,粒子的速度限定分别为Vmax=0.6、Vmin=-0.6。
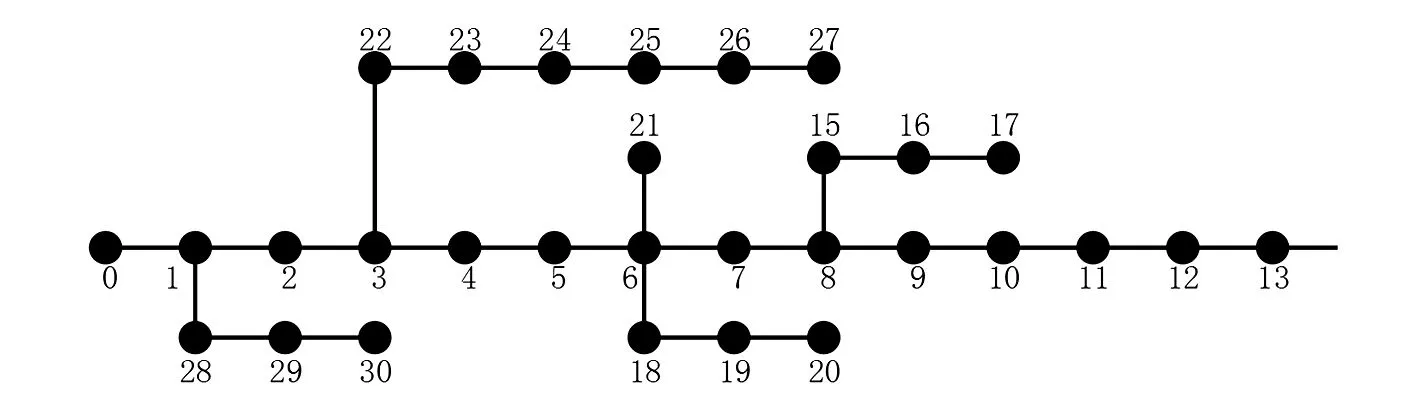
图4 IEEE 30算例系统接线

支路序号支路电阻/Ω支路电抗/Ω有功负荷/kW无功负荷/kVA0-10.1960.655001-20.2790.0155221742-30.4440.439003-40.8640.7519363124-50.8640.751005-61.3740.774006-71.3740.774007-81.3740.774008-91.3740.774189639-101.3740.7740010-111.3740.77433611211-121.3740.77465721912-131.3740.77478326113-141.3740.7747292438-150.8640.77447715915-161.3740.77454918316-171.3740.7744771596-180.8640.75134211418-190.8640.75167222419-201.3740.7744951656-210.8640.751207693-220.4440.43952217422-230.4440.439191763923-240.8640.7510024-250.8640.751111637225-260.8640.75157918326-271.3740.7747922641-280.2790.01588229428-291.3740.77488229429-301.3740.774882294
首先计算出算例优化前系统的有功网损为1.059 9 MW, 最低电压为19.283 5 kV,出现在14号节点。配电网采用改进的粒子群无功优化算法后,其具体结果如分析如下:
1)先不考虑罚函数影响,即不考虑节点电压越限和无功补偿容量越限的问题,取λ1=λ2=0。
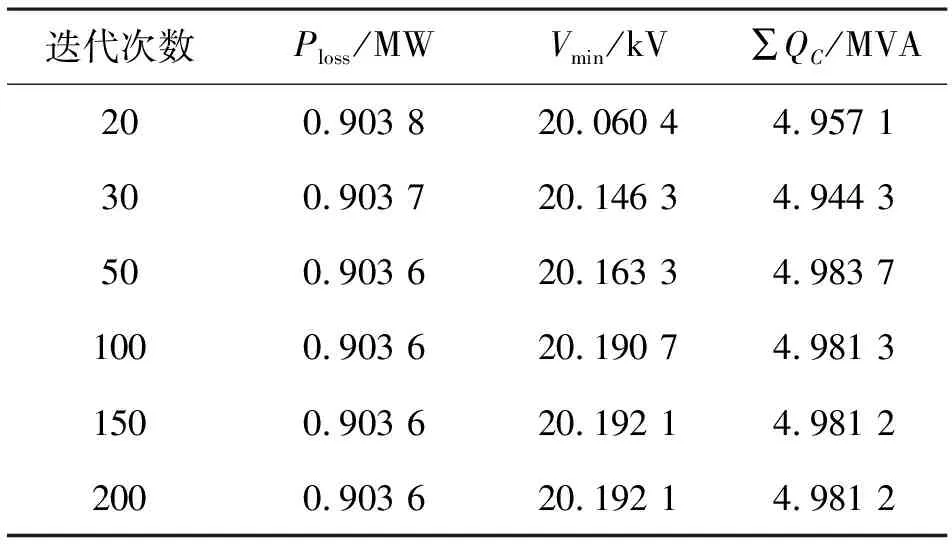
表2 BPSO算法无功优化结果(λ1=λ2=0)
表2中:Ploss为系统的有功网损值;Vmin为在完成迭代时(即系统达到有功网损最小时)系统节点电压的最低值;∑QC为系统在达到有功网损最小时补偿装置向系统提供的总的补偿容量。
通过分析可得,当迭代次数设为50时,系统有功网损已到达最低值,即粒子已经寻得全局最优解;随着迭代次数的增加,系统的节点电压有所改善,同时补偿容量有所增加。由表2可看出,当迭代次数为100时,系统已有较好的电压,并且随着迭代次数的增加对系统节点电压的改善变小。可得出当迭代次数设为100时,系统有较好的优化结果。
2)取最大迭代次数Tmax=100,不考虑补偿容量越限的限制,即将罚因子λ2设为0,考虑罚因子λ1取不同的值对优化结果的影响。
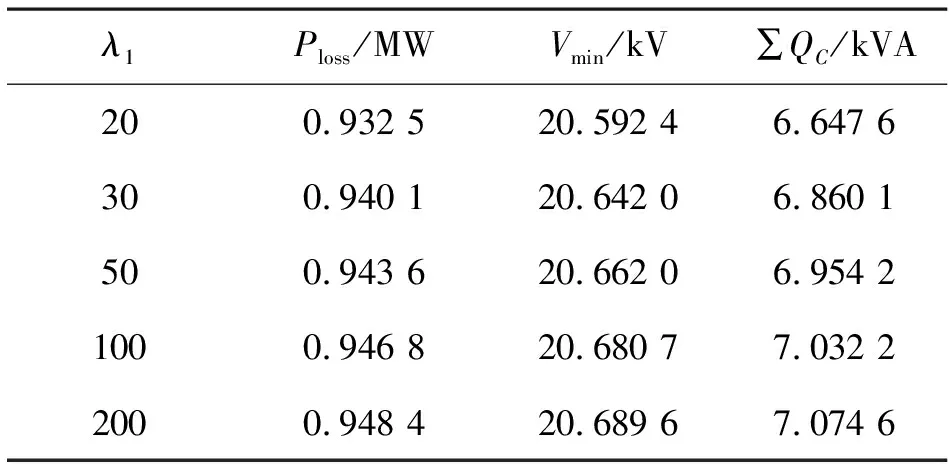
表3 BPSO算法无功优化结果(λ2=0,λ1任意取值)
由表3可以看出,当罚因子λ1的取值越来越大时,系统的节点电压越来越好,但是系统的有功网损也越来越高,同时补偿容量也越来越大。综合考虑,当λ1=10时系统可以获得比较好的解。
3)取最大迭代次数Tmax=100,不考虑节点电压越限的限制,即将罚因子λ1设为0,考虑罚因子λ2取不同的值时对优化结果的影响。
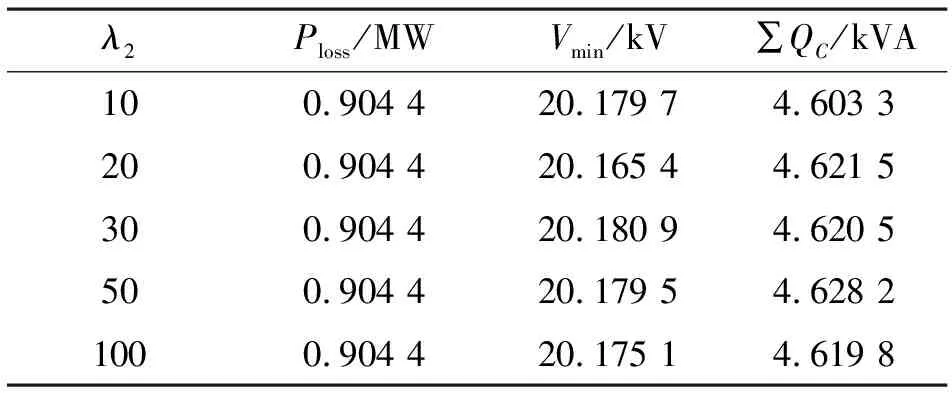
表4 BPSO算法无功优化结果(λ1=0,λ2任意取值)
由表4分析可得,当λ2取不同值时,系统有功网损值不变,综合考虑节点电压质量及无功补偿容量,可知当λ2=10时系统有比较好的解。
综上所述,在对IEEE 30节点配电网进行无功优化时,选取迭代次数Tmax=100,惩罚因子λ1、λ2都取10时,优化效果最佳。
4.2 BPSO算法最优补偿
在算例配电网无功优化过程中,选取迭代次数Tmax=100,惩罚因子λ1=λ2=10时,采用BPSO算法对系统无功优化。可以得到:系统有功网损Ploss为0.906 7 MW,最低节点电压值Vmin为20.286 5 kV,系统补偿总容量∑QC为4.980 4 MVA。
为验证BPSO算法的优越性,在相同条件下运行常规PSO算法和BPSO算法,得到电压曲线比较如图5所示,可以看出:PSO算法和BPSO算法对配电网电压质量都起到明显改善作用,但BPSO相对电压曲线更趋稳定,优化效果更好。

图5 PSO和BPSO算法电压曲线比较
常规PSO算法和BPSO算法的网损优化结果见表5,有功网损的收敛曲线如图6所示。
通过对PSO、BPSO两种算法的无功优化结果的比较,可以得出:
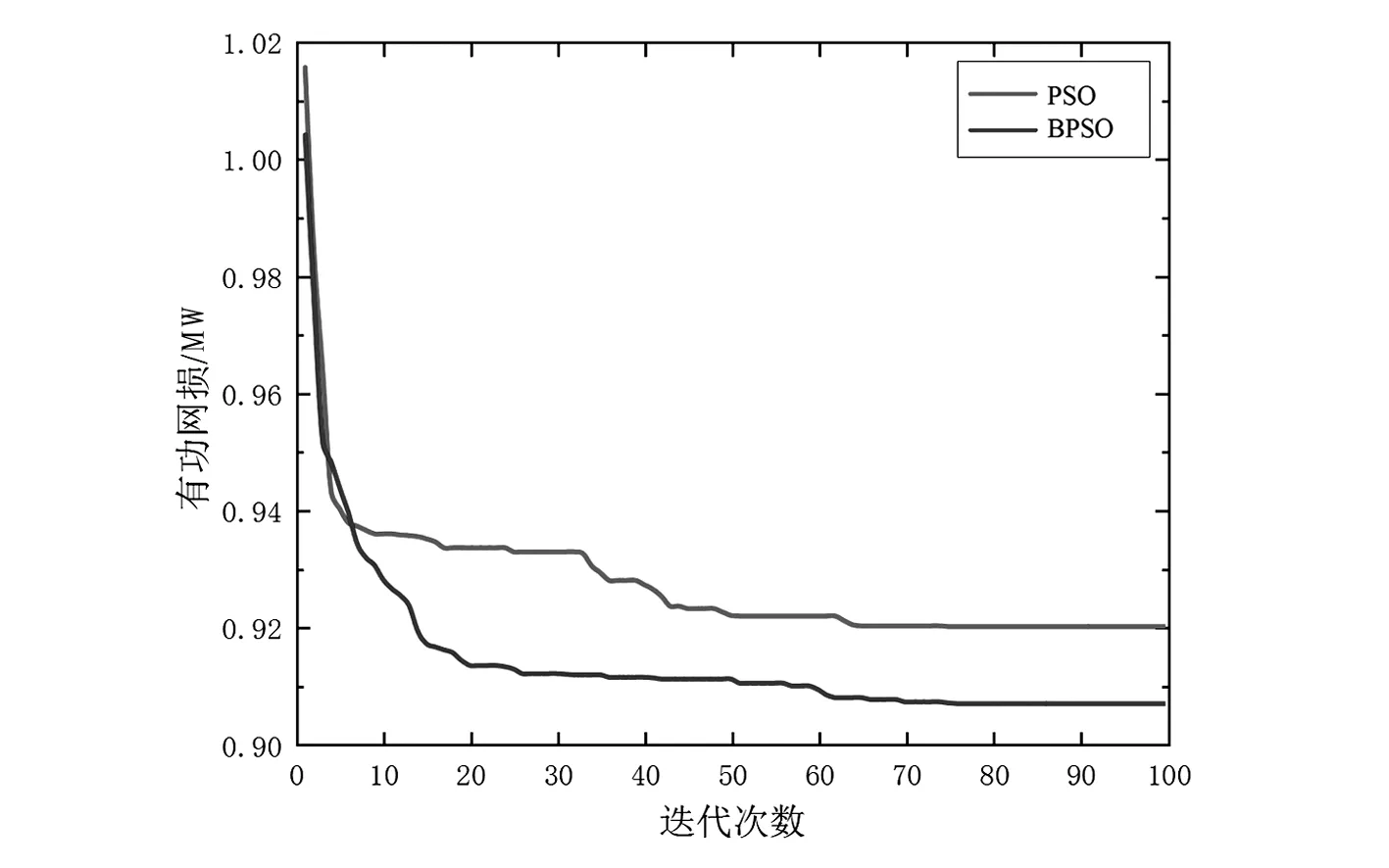
图6 PSO和BPSO的收敛曲线
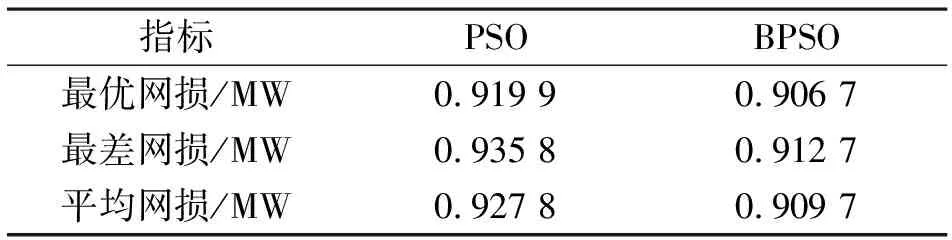
表5 优化结果比较
1)PSO算法在对配电网无功优化过程中,往往会陷入局部最优值,导致优化停滞不前;
2)BPSO算法在前期优化时,收敛速度与精度都表现不错,且随着迭代次数增加,回溯迭代使得搜索区间缩减,收敛速度变快,收敛精度也大幅提升;
3)通过两种算法的无功优化,配电网系统的有功网损值都得到大幅降低,但BPSO算法优化后的有功网损值相比PSO算法较小。
5 结 语
针对配电网节点多、结构复杂的特点,在充分考虑有功网损、电压质量和无功补偿设备容量限制的基础上,选取合适的优化目标函数,通过基于回溯迭代的粒子群算法对IEEE 33节点配电网系统进行无功优化,并验证该方法的可行性。主要结论如下:
1)在配电网无功优化过程中,合理地选取有功网损、电压质量和无功补偿设备容量作为优化目标函数,优化效果更优越;
2)BPSO优化算法与常规的粒子群算法相比,其收敛速度与精度都具有较好的效果,且优化后的有功网损幅值得到一定改善。
