MMC-MTDC输电系统频率协调控制策略
2019-04-01,,,
,,,
(1.国网四川省电力公司南充供电公司,四川 南充 637000;2.四川大学电气信息学院,四川 成都 610065)
0 引 言
在实现交流系统异步连接和新能源大规模集中功率送出等方面,基于模块化多电平换流器的多端直流系统是一套具有前景的解决方案[1-2]。多端系统在增加系统传输容量、对所连接的交流系统实现无功支撑、提升区域频率稳定和加强交流系统暂态稳定等方面都具有很大的优势[3-5]。为了克服远方新能源发电区域与负荷中心的长距离输电容量的挑战,MMC-MTDC技术提供了高效灵活可控的大容量传输解决方案。此外,未来不同国家和地区的电力系统互联可由MMC-MTDC技术不断提升传输容量得以实现,这为不同国家和区域的能源交易市场铺平了道路,例如中国的张北直流工程和欧洲超级电网工程。MMC-MTDC不仅能够交换确定的传输容量,而且当交流系统功率不平衡导致频率不稳定时,可以利用其实现异步交流系统的旋转储备功率交换来提升系统频率稳定。这个特点使其在传统电厂大量退出和新能源集中接入电网的新时代电力系统背景下扮演了十分重要的角色。下面的研究重点是基于MMC-MTDC提出不同的附加频率控制策略来提升交流系统的频率稳定。
考虑到MTDC输电网络的容量传输等级相对较大,因此异步交流网络可以通过MTDC系统来实现一次频率的调整。目前已经有大量基于VSC型平均值换流器模型进行一次频率调整的研究文献,VSC-HVDC通常输出为两电平,直流侧单一的直流电容对直流电压的动态特性影响较大。此外,平均值模型的交直流侧功率平衡是直接耦合的,而MMC结构中大量子模块电容的储能作用可以认为交直流侧功率是解耦的。文献[6-8]中介绍了MTDC输电系统的实时功率平衡是通过直流电压下垂控制策略来实现的,直流电压下垂控制策略的优势在于,当网络中潮流出现较大的波动时,如一个换流站退出运行,其可以利用多个换流站来分担不平衡功率。这也为风电场利用MTDC进行功率输送时解决功率波动提供了一个较好方案。文献[9]在VSC-MTDC控制器中引入了直流电压下垂与频率下垂控制结构,该策略易于通过MTDC实现异步联网交流系统的一次频率调整。文献[10]研究了VSC-HVDC在异步电网中的频率调节功能,分别讨论了固定频率控制、直流电压-频率控制、功率-频率控制3种控制方法,对通过MTDC连接的异步电网的频率协调控制具有借鉴和指导意义。文献[11]针对MMC-HVDC提出了4种频率一次调整控制策略,然而该策略在MTDC系统中会使得定直流电压的换流站承担所有的不平衡功率,在多端系统中该策略会威胁系统的稳定运行。
针对MMC-MTDC直流电网参与异步交流系统一次频率调整的文献较少以及目前的文献侧重于两端系统频率附加控制策略的研究,就MMC-MTDC输电系统提出了3种频率协调控制策略来实现异步交流区域的功率支撑和频率协调。
1 测试系统
为了研究基于MMC-MTDC输电系统的频率协调控制策略,在文献[12-14]的IEEE 39节点系统基础上进行改进,如图1所示。图中删除了部分交流线路,原来的系统分离成由MMC-MTDC连接的4个异步交流系统。改进后的交直流系统是由345 kV的交流输电网和500 kV的四端直流电网共同构成,4个换流站分别连接于母线5、母线6、母线17、母线26。仿真平台相关系统模块说明如下:

图1 含有MMC-MTDC的改进IEEE 39节点系统
1)每个发电机采用dq0坐标系下的模型进行研究,且发电机的机械系统运用单质量块进行等值;
2)每个发电机的调速器和涡轮机单元采用仿真软件中的HGOV18模型;
3)交直流系统的线路采用Bergeron模型;
4)发电机励磁系统采用IEEE DC1A 型模型;
5)负荷采用式(1)的模型进行等值。
(1)
式中:P、Q、V为有功功率、无功功率、交流电压;P0、Q0、V0为额定有功功率、额定无功功率、额定电压;NP和NQ为有功、无功的电压因子;KPF和KQF为有功、无功的频率因子。取NP=NQ=2,KPF=KQF=0。
2 MMC数学模型
MMC型换流站的桥臂由上百个子模块构成,在系统仿真时需要大量的计算时间。交直流系统研究中为了加快仿真速度和节省仿真空间,通常采用文献[15]的CIGRE B4.57导则中Type 4模型。该模型将所有桥臂的子模块输出电压用受控电压源进行等效,交直流物理量如图2所示。这里MMC的控制结构参照文献[16-17]中VSC-MTDC的频率协调控制结构,为此可以在MMC-MTDC的相关控制结构中引入一次频率调制的附加控制策略。

图2 MMC等值电路
根据图2的等值电路列写基尔霍夫电流、电压定律(下标i=a、b、c):
ii=ipi-ini
(2)
(3)
(4)
式中:ip、in为换流器上、下桥臂电流;up、un为换流器上、下桥臂电压;Rarm、Larm为桥臂电阻和桥臂电抗;ui、ii为交流侧输出电压、电流;Udc为直流电压。
联立式(2)至式(4),定义内部电流为iz,交流侧控制电压为uΔ,直流侧控制电压为uz,可得
iz=(ipi+ini)/2
(5)
(6)
(7)
在同步旋转dq坐标系下,交流侧的功率通过控制uΔ来实现对交流电流ii的控制,而直流侧的功率和电压通过uz来调整内部电流iz的零序成分(稳态下,3iz0=Idc)。换流站与PCC点之间换流变压器的Y/Δ连接方式使得换流站阀侧交流电流的零序分量不存在,剩余分量通过Clarke变换获得电流的水平分量和垂直分量[18]。根据瞬时无功功率理论,可得交直流交换的功率在dq坐标下的有功和无功为
(8)
式中:Usd、isd为派克变换后的d轴电压、电流;Usq、isq为派克变换后的q轴电压、电流。
为了达到设定的功率运行点,MMC外环控制器的电流分量由式(9)进行调整。
(9)

(10)
式中:Prefm为PCC点测量的有功功率;Pref为有功功率参考值;KP、KI为比例积分系数。有功功率的参考值是通过调度中心给定,为了使MMC换流站参与频率的调整,可以在外环控制器中叠加一个关于频率的功率分量。
3 交流系统的一次频率调整
交流电网的频率稳定是所有交流电网稳定运行的前提,发电机组和负荷之间功率暂态平衡通过频率变化来反应。不考虑严重情况下的二次调频,交流电网的一次频率调整是通过主调频发电厂调速器的频率下垂控制来实现的,其控制原理是将频率作为全局变量来平衡交流电网的功率交换。
发电机的频率下垂控制结构如图3所示,其详细的下垂特性和结构参考文献[19-20]。频率下垂系数ρac的大小表示发电机在交流电网功率不平衡导致频率偏移时的补偿能力。在图5中,频率下垂系数越小,交流系统就越强。典型的频率下垂系数为0.04~0.08 p.u.。

图3 发电机组频率下垂控制
交流电网中频率响应与发电机和负荷的调节特性相关,其功率静态特性曲线如图4所示。交流电网初始运行点A,由于负荷的变化,经过功频调整后运行于B,其功率增量为
ΔPD0=-(KG+KD)Δf=-KΔf
(11)
式中:KG、KD、K分别为发电机功频静态特性系数、负荷频率调节效应系数以及交流系统功频静态特性系数。

图4 交流系统功率-频率静态特性
4 MMC-MTDC一次频率协调控制策略
通过多端系统连接的异步交流电网,如果采用主从控制策略,则只有一个换流站控制整个直流网络的直流电压(该换流站母线称为松弛节点)。交流系统出现频率变化时,采用定功率的MMC不能对频率变化进行响应,为此在功率参考值中引入频率变化带来的功率变化量ΔPF,可以使MMC换流站参与交流系统的一次频率调整。如果交流系统的频率偏差过大,则可以通过MTDC系统实现异步电网功率支撑和频率稳定。MTDC系统中实现区域功率支撑需要引入直流电压下垂控制策略,其工作原理与交流系统中发电机的功频静态特性相似,将会产生一个与直流电压相关的功率变化量ΔPDC。
4.1 直流电压下垂控制

图5 直流电压下垂控制结构

ΔUDC=UDCref-UDCm
(12)
ΔPDC=KDCΔUDC
(13)
采用直流电压下垂的换流站共同协调网络的直流电压,当直流网络中出现不平衡功率时,以直流电压作为纽带,通过换流站的下垂系数来实现不平衡功率在换流站之间的分配,从而减轻了主从控制中直流电压站的负担。
4.2 频率协调控制策略
4.2.1 固定频率控制
固定频率控制策略类似于传统同步发电机的一次频率调整。实际测量到的换流站PCC点的频率fPCCm与额定固定参考频率fref的偏差乘以一个下垂系数KF,得到一个具有比例特性的额外功率增量ΔPF,这个功率增量叠加至4.1中直流电压下垂的输出量中,即可得到新的功率增量,从而实现了MTDC系统的电压下垂和频率下垂控制,其结构如图6所示。
采用固定频率控制策略,通常对于一个具有较高短路比的强交流系统来说,当交流系统出现较大的功率不平衡情况时,通过MMC-MTDC可以很好地支撑弱交流系统的稳定。通常额定频率在标幺制下设为fref=1,此时式(10)中的功率参考值由式(16)进行更新。
Δf=fref-fPCCm
(14)
ΔPF=KFΔf
(15)

=Pref-ΔPF+ΔPDC
(16)

图6 基于电压下垂的固定频率控制结构
4.2.2 频率偏差PI控制

(17)
每个换流站频率调制引入附加功率为

(18)


图7 频率偏差PI控制结构
4.2.3 功率估算频率控制
交流系统中负荷的变化量通常很难估计,为此提出根据频率的变化量利用功频特性系数进行交流侧功率变化量的估计,然后根据功率变化量来调整MMC换流站的附加功率。根据MMC换流站在频率协调控制中扮演的角色,叠加频率相关的功率分量至其外环控制器。非频率事故的交流系统通过MMC-MTDC实现频率支撑时的附加功率与该交流系统的功-频特性系数正相关,故可利用功-频静特性系数之比来决定换流站的功率支撑比例。其实现过程如图8所示,其中:Ki表示频率故障端的功-频特性系数;α(α∈[0,1])表示需要调制的功率的范围;非频率故障的模块中的βn表示第n个换流站所占支撑功率的比例。其满足如下表达式:
β1∶β2∶…∶βn=K1∶K2∶…∶Kn
(19)

图8 功率估算频率控制结构
5 仿真分析
为了验证所提出的频率协调控制策略在基于MMC-MTDC的交直流系统中的控制效果,将所提的各种控制方法运用于仿真算例中进行研究。在图1的区域1中加入450 MW的负荷,由于负荷的增加将导致区域1的频率下降,为了减小区域1的频率变化量,通过MMC-MTDC来实现区域间的功率支撑和频率协调。系统仿真参数如表1至表4所示。

表1 交流系统功-频静特性系数
算例1:直流电压下垂控制
为了验证频率协调控制策略的有效性,以电压下垂控制在频率故障中的响应特性为参照,t=2 s时,在区域1中交流母线母线3处加入450 MW的负荷。从表1中的K1可以获得频率的理论变化量为-0.29 Hz。通过图9的仿真结果可以看出,区域1的频率下降至49.71 Hz左右,其他交流区域频率无变化。传输的有功功率和直流电压均无变化,说明直流电压下垂控制策略无法实现交流系统间频率变化时的功率支撑和频率协调,无法利用具有备用容量系统的功率支撑,这给系统的稳定运行带来了风险。

表2 换流站系统参数

表3 发电机参数

表4 直流线路参数

图9 直流电压下垂控制策略
算例2:固定频率控制
如图10所示,在t=2 s之前,交流系统的频率以额定频率运行。在2 s时负荷的增加使得区域1的频率下降,由于MMC-MTDC采用的是频率协调控制策略,区域1的频率下降使得MMC1换流站的功率参考值增加,直流电压下垂控制策略使得其余换流站进行功率支撑,从而导致参与功率支撑的交流系统的频率下降。区域1的频率在稳定运行后频率维持在49.80 Hz左右,MMC1的传输功率提升了150 MW左右,由于MMC2、MMC3、MMC4传输的功率都分别增加了33 MW、41 MW、91 MW,使得各交流系统频率相应下调,换流器损耗和线路损耗产生了15 MW的功率缺额。直流电压下垂系数KDC=3,导致直流电压的下降幅度较大。仿真结果表明,该控制策略能够有效地通过MMC-MTDC系统实现区域间的功率支撑和频率协调。
算例3:频率偏差PI控制


图10 固定频率控制策略

图11 频率偏差PI控制
算例4: 功率估算频率控制
基于功率估算的频率协调控制策略对应的仿真结果见图12、图13和图14,分别对应于α=1/3、α=2/3、α=1。该策略通过实时采集区域1的频率变化,根据频率的变化量利用功-频静特性系数来估算交流系统的功率变化量,将该功率量叠加至MMC1的外环控制器,并将该分量按照K2∶K3∶K4=0.25∶0.17∶0.58的比例分别叠加至MMC2、MMC3、MMC4的外环控制器中。通过调整α的值实现非事故区域对区域1的频率支撑和频率协调。仿真结果表明通过控制α的大小可以不同程度地实现异步电网频率协调控制策略,更好地利用交流系统的旋转备用容量。采用频率协调控制的换流站根据功频静特性系数大小决定附加功率,该方法可以有效地防止功频静特性系数较小的交流系统实现功率支撑时引起较大的频率偏移,故该方法在异步联网系统中具有较好的适用性。

图12 α=1/3时功率估算频率控制

图13 α=2/3时功率估算频率控制
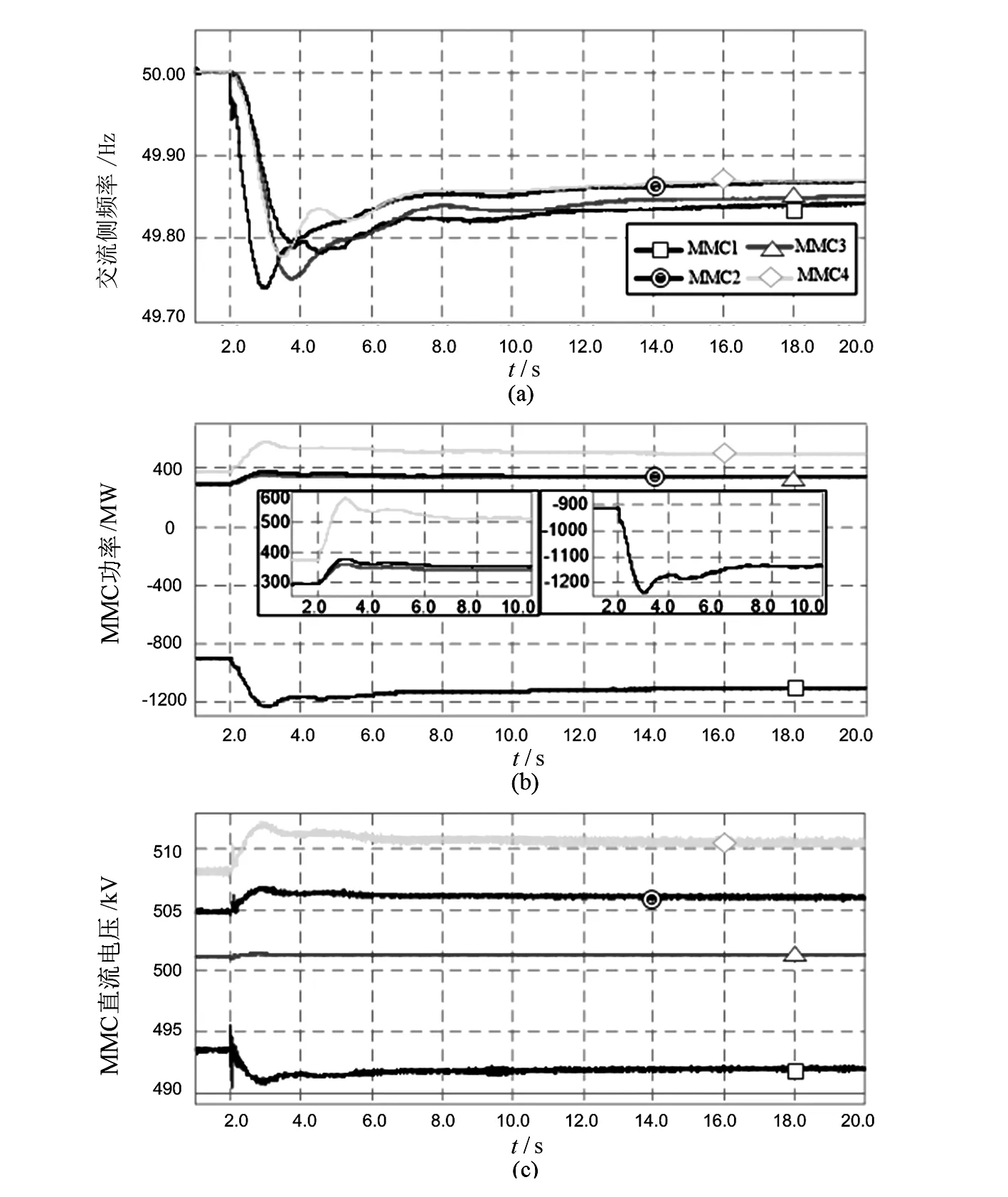
图14 α=1时功率估算频率控制
6 结 语
前面提出了3种基于MMC-MTDC输电系统的频率协调控制策略的方法。该控制策略在MMC异步联网时实现不同区域的功率支撑和频率协调,根据频率变化自动调整MMC的传输功率。固定频率控制中控制器输入的参考值为额定值,在交直流区域同步中具有优势,在异步联网中适用于功频特性系数较大的交流系统。频率偏差PI控制方法中由于频率的参考值进行了全局处理,可以较好地实现异步交流系统频率的实时跟踪控制,在实现区域功率支撑时,频率稳定特性良好。功率估算频率控制的方法具有更好的适用性,在实际系统中负荷变化一般是不明确的,测量的频率变化可以反映出功率缺额,为此利用交流系统的频率支撑能力来设置换流站的功率支撑量,换流站可以更为合理地分配网络不平衡功率。
